20.1: Solid triangles

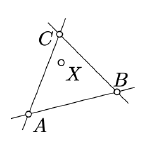
We say that the point \(X\) lies inside a nondegenerate triangle \(ABC\) if the following three condition hold:

• \(A\) and \(X\) lie on the same side of the line \((BC)\);
• \(B\) and \(X\) lie on the same side of the line \((CA)\);
• \(C\) and \(X\) lie on the same side of the line \((AB)\).

The set of all points inside \(\triangle ABC\) and on its sides \([AB]\), \([BC]\), \([CA]\) will be called solid triangle \(ABC\) and denoted by \(\blacktriangle ABC\).

Exercise \(\PageIndex{1}\)

Show that any solid triangle is convex; that is, for any pair of points \(X,Y\in\blacktriangle ABC\), then the line segment \([XY]\) lies in \(\blacktriangle ABC\).

Hint

Assume the contrary; that is, there is a point \(W \in [XY]\) such that \(W \not\in \blacktriangle ABC\).

Without loss of generality, we may assume that W and A lie on the opposite sides of the line \((BC)\).

It imples that both segments \([W X]\) and \([W Y]\) intersect \((BC)\). By Axiom II, \(W \in (BC)\) — a contradiction.

The notations \(\triangle ABC\) and \(\blacktriangle ABC\) look similar, they also have close but different meanings, which better not to confuse. Recall that \(\triangle ABC\) is an ordered triple of distinct points (see page ), while \(\blacktriangle ABC\) is an infinite set of points.

In particular, \(\blacktriangle ABC=\blacktriangle BAC\) for any triangle \(ABC\). Indeed, any point that belongs to the set \(\blacktriangle ABC\) also belongs to the set \(\blacktriangle BAC\) and the other way around. On the other hand, \(\triangle ABC \ne \triangle BAC\) simply because the ordered triple of points \((A,B,C)\) is distinct from the ordered triple \((B,A,C)\).

Note that \(\blacktriangle ABC\cong\blacktriangle BAC\) even if \(\triangle ABC\ncong\triangle BAC\), where congruence of the sets \(\blacktriangle ABC\) and \(\blacktriangle BAC\) is understood the following way:

Definition \(\PageIndex{1}\)

Two sets \(\mathcal{S}\) and \(\mathcal{T}\) in the plane are called congruent (briefly \(\mathcal{S}\cong \mathcal{T}\)) if \(\mathcal{T}=f(\mathcal{S})\) for some motion \(f\) of the plane.

If \(\triangle ABC\) is not degenerate and

\(\blacktriangle ABC\cong \blacktriangle A'B'C',\)

then after relabeling the vertices of \(\triangle ABC\) we will have

\(\triangle ABC\cong \triangle A'B'C'.\)

Indeed it is sufficient to show that if \(f\) is a motion that maps \(\blacktriangle ABC\) to \(\blacktriangle A'B'C'\), then \(f\) maps each vertex of \(\triangle ABC\) to a vertex \(\triangle A'B'C'\). The latter follows from the characterization of vertexes of solid triangles given in the following exercise:

Exercise \(\PageIndex{1}\)

Let \(\triangle ABC\) be nondegenerate and \(X\in \blacktriangle ABC\). Show that \(X\) is a vertex of \(\triangle ABC\) if and only if there is a line \(\ell\) that intersects \(\blacktriangle ABC\) at the single point \(X\).

Hint

To prove the "only if" part, consider the line passing thru the vertex that is parallel to the opposite side.

To prove the "if" part, use Pasch’s theorem (Theorem 3.4.1).