1.9: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercises
Graphically, find the point (x1,y1) which lies on both lines, x+3y=1 and 4x−y=3. That is, graph each line and see where they intersect.
- Answer
-
x+3y=14x−y=3, Solution is: [x=1013,y=113].
Graphically, find the point of intersection of the two lines 3x+y=3 and x+2y=1. That is, graph each line and see where they intersect.
- Answer
-
3x+y=3x+2y=1, Solution is: [x=1,y=0]
Do the three lines, x+2y=1, 2x−y=1, and 4x+3y=3 have a common point of intersection? If so, find the point and if not, tell why they don’t have such a common point of intersection.
- Answer
-
x+2y=12x−y=14x+3y=3, Solution is: [x=35,y=15]
Do the three planes, x+y−3z=2, 2x+y+z=1, and 3x+2y−2z=0 have a common point of intersection? If so, find one and if not, tell why there is no such point.
- Answer
-
No solution exists. You can see this by writing the augmented matrix and doing row operations. [11−32211132−20], row echelon form: [104001−700001]. Thus one of the equation says 0=1 in an equivalent system of equations.
Four times the weight of Gaston is 150 pounds more than the weight of Ichabod. Four times the weight of Ichabod is 660 pounds less than seventeen times the weight of Gaston. Four times the weight of Gaston plus the weight of Siegfried equals 290 pounds. Brunhilde would balance all three of the others. Find the weights of the four people.
- Answer
-
4g−I=1504I−17g=−6604g+s=290g+I+s−b=0, Solution is: {g=60,I=90,b=200,s=50}
Consider the following augmented matrix in which ∗ denotes an arbitrary number and ◼ denotes a nonzero number. Determine whether the given augmented matrix is consistent. If consistent, is the solution unique? [◼∗∗∗∗∗0◼∗∗0∗00◼∗∗∗0000◼∗]
- Answer
-
The solution exists but is not unique.
Consider the following augmented matrix in which ∗ denotes an arbitrary number and ◼ denotes a nonzero number. Determine whether the given augmented matrix is consistent. If consistent, is the solution unique? [◼∗∗∗0◼∗∗00◼∗]
- Answer
-
A solution exists and is unique.
Consider the following augmented matrix in which ∗ denotes an arbitrary number and ◼ denotes a nonzero number. Determine whether the given augmented matrix is consistent. If consistent, is the solution unique? [◼∗∗∗∗∗0◼0∗0∗000◼∗∗0000◼∗]
Consider the following augmented matrix in which ∗ denotes an arbitrary number and ◼ denotes a nonzero number. Determine whether the given augmented matrix is consistent. If consistent, is the solution unique? [◼∗∗∗∗∗0◼∗∗0∗0000◼00000∗◼]
- Answer
-
There might be a solution. If so, there are infinitely many.
Suppose a system of equations has fewer equations than variables. Will such a system necessarily be consistent? If so, explain why and if not, give an example which is not consistent.
- Answer
-
No. Consider x+y+z=2 and x+y+z=1.
If a system of equations has more equations than variables, can it have a solution? If so, give an example and if not, tell why not.
- Answer
-
These can have a solution. For example, x+y=1,2x+2y=2,3x+3y=3 even has an infinite set of solutions.
Find h such that [2h4367] is the augmented matrix of an inconsistent system.
- Answer
-
h=4
Find h such that [1h3246] is the augmented matrix of a consistent system.
- Answer
-
Any h will work.
Find h such that [1143h12] is the augmented matrix of a consistent system.
- Answer
-
Any h will work.
Choose h and k such that the augmented matrix shown has each of the following:
- one solution
- no solution
- infinitely many solutions
[1h224k]
- Answer
-
If h≠2 there will be a unique solution for any k. If h=2 and k≠4, there are no solutions. If h=2 and k=4, then there are infinitely many solutions.
Choose h and k such that the augmented matrix shown has each of the following:
- one solution
- no solution
- infinitely many solutions
[1222hk]
- Answer
-
If h≠4, then there is exactly one solution. If h=4 and k≠4, then there are no solutions. If h=4 and k=4, then there are infinitely many solutions.
Determine if the system is consistent. If so, is the solution unique? x+2y+z−w=2x−y+z+w=12x+y−z=14x+2y+z=5
- Answer
-
There is no solution. The system is inconsistent. You can see this from the augmented matrix. [121−121−111121−10142105], reduced row-echelon form: [100130010−2300010000001].
Determine if the system is consistent. If so, is the solution unique? x+2y+z−w=2x−y+z+w=02x+y−z=14x+2y+z=3
- Answer
-
Solution is: [w=32y−1,x=23−12y,z=13]
Determine which matrices are in reduced row-echelon form.
- [120017]
- [100000120000]
- [110005001204000013]
- Answer
-
- This one is not.
- This one is.
- This one is.
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [2−13−110211−11−2]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [00−1−11110110−1]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [3−6−7−81−2−2−21−2−3−4]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [2451512391226]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [4−171010331−1−21]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [35−4212−1111−20]
Row reduce the following matrix to obtain the row-echelon form. Then continue to obtain the reduced row-echelon form. [−23−871−25−51−37−8]
Find the solution of the system whose augmented matrix is [120213421021]
Find the solution of the system whose augmented matrix is [120220113213]
- Answer
-
The reduced row-echelon form is [10121201−14340000]. Therefore, the solution is of the form z=t,y=34+t(14),x=12−12t where t∈R.
Find the solution of the system whose augmented matrix is [11011042]
- Answer
-
The reduced row-echelon form is [104201−4−1] and so the solution is z=t,y=4t,x=2−4t.
Find the solution of the system whose augmented matrix is [102112010121120013101022]
- Answer
-
The reduced row-echelon form is [1000930100−400010−7−1000161] and so x5=t,x4=1−6t,x3=−1+7t,x2=4t,x1=3−9t.
Find the solution of the system whose augmented matrix is [1021120101210200131−12220]
- Answer
-
The reduced row-echelon form is [1020−125201001232000132−12000000]. Therefore, let x5=t,x3=s. Then the other variables are given by x4=−12−32t,x2=32−t12,,x1=52+12t−2s.
Find the solution to the system of equations, 7x+14y+15z=22, 2x+4y+3z=5, and 3x+6y+10z=13.
- Answer
-
Solution is: [x=1−2t,z=1,y=t]
Find the solution to the system of equations, 3x−y+4z=6, y+8z=0, and −2x+y=−4.
- Answer
-
Solution is: [x=2−4t,y=−8t,z=t]
Find the solution to the system of equations, 9x−2y+4z=−17, 13x−3y+6z=−25, and −2x−z=3.
- Answer
-
Solution is: [x=−1,y=2,z=−1]
Find the solution to the system of equations, 65x+84y+16z=546, 81x+105y+20z=682, and 84x+110y+21z=713.
- Answer
-
Solution is: [x=2,y=4,z=5]
Find the solution to the system of equations, 8x+2y+3z=−3,8x+3y+3z=−1, and 4x+y+3z=−9.
- Answer
-
Solution is: [x=1,y=2,z=−5]
Find the solution to the system of equations, −8x+2y+5z=18,−8x+3y+5z=13, and −4x+y+5z=19.
- Answer
-
Solution is: [x=−1,y=−5,z=4]
Find the solution to the system of equations, 3x−y−2z=3, y−4z=0, and −2x+y=−2.
- Answer
-
Solution is: [x=2t+1,y=4t,z=t]
Find the solution to the system of equations, −9x+15y=66,−11x+18y=79, −x+y=4, and z=3.
- Answer
-
Solution is: [x=1,y=5,z=3]
Find the solution to the system of equations, −19x+8y=−108, −71x+30y=−404, −2x+y=−12, 4x+z=14.
- Answer
-
Solution is: [x=4,y=−4,z=−2]
Suppose a system of equations has fewer equations than variables and you have found a solution to this system of equations. Is it possible that your solution is the only one? Explain.
- Answer
-
No. Consider x+y+z=2 and x+y+z=1.
Suppose a system of linear equations has a 2×4 augmented matrix and the last column is a pivot column. Could the system of linear equations be consistent? Explain.
- Answer
-
No. This would lead to 0=1.
Suppose the coefficient matrix of a system of n equations with n variables has the property that every column is a pivot column. Does it follow that the system of equations must have a solution? If so, must the solution be unique? Explain.
- Answer
-
Yes. It has a unique solution.
Suppose there is a unique solution to a system of linear equations. What must be true of the pivot columns in the augmented matrix?
- Answer
-
The last column must not be a pivot column. The remaining columns must each be pivot columns.
The steady state temperature, u, of a plate solves Laplace’s equation, Δu=0. One way to approximate the solution is to divide the plate into a square mesh and require the temperature at each node to equal the average of the temperature at the four adjacent nodes. In the following picture, the numbers represent the observed temperature at the indicated nodes. Find the temperature at the interior nodes, indicated by x,y,z, and w. One of the equations is z=0.05in14(10+0+w+x).
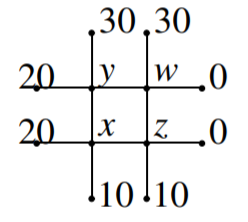
- Answer
-
You need 14(20+30+w+x)−y=014(y+30+0+z)−w=014(20+y+z+10)−x=014(x+w+0+10)−z=0, Solution is: [w=15,x=15,y=20,z=10].
Find the rank of the following matrix. [4−16−1−51−40−11−4−1−2]
Find the rank of the following matrix. [3651212251212]
Find the rank of the following matrix. [00−1031410−814012−1−40−1−2]
Find the rank of the following matrix. [4−43−91−11−21−10−3]
Find the rank of the following matrix. [20101101001001710017]
Find the rank of the following matrix. [415291481353915]
Find the rank of the following matrix. [00−101123−2−18122−1−11−1−2−2111]
Find the rank of the following matrix. [1−203111−204151−2031100000]
Find the rank of the following matrix. [−2−3−2111101−30−3]
Find the rank of the following matrix. [4420−11711505115−123315−36]
Find the rank of the following matrix. [−134−381−3−42−51−3−41−2−268−24]
Suppose A is an m×n matrix. Explain why the rank of A is always no larger than min(m,n).
- Answer
-
It is because you cannot have more than min(m,n) nonzero rows in the reduced row-echelon form. Recall that the number of pivot columns is the same as the number of nonzero rows from the description of this reduced row-echelon form.
State whether each of the following sets of data are possible for the matrix equation AX=B. If possible, describe the solution set. That is, tell whether there exists a unique solution, no solution or infinitely many solutions. Here, [A|B] denotes the augmented matrix.
- A is a 5×6 matrix, rank(A)=4 and rank[A|B]=4.
- A is a 3×4 matrix, rank(A)=3 and rank[A|B]=2.
- A is a 4×2 matrix, rank(A)=4 and rank[A|B]=4.
- A is a 5×5 matrix, rank(A)=4 and rank[A|B]=5.
- A is a 4×2 matrix, rank(A)=2 and rank[A|B]=2.
- Answer
-
- This says B is in the span of four of the columns. Thus the columns are not independent. Infinite solution set.
- This surely can’t happen. If you add in another column, the rank does not get smaller.
- This says B is in the span of the columns and the columns must be independent. You can’t have the rank equal 4 if you only have two columns.
- This says B is not in the span of the columns. In this case, there is no solution to the system of equations represented by the augmented matrix.
- In this case, there is a unique solution since the columns of A are independent.
Consider the system −5x+2y−z=0 and −5x−2y−z=0. Both equations equal zero and so −5x+2y−z=−5x−2y−z which is equivalent to y=0. Does it follow that x and z can equal anything? Notice that when x=1, z=−4, and y=0 are plugged in to the equations, the equations do not equal 0. Why?
- Answer
-
These are not legitimate row operations. They do not preserve the solution set of the system.
Balance the following chemical reactions.
- KNO3+H2CO3→K2CO3+HNO3
- AgI+Na2S→Ag2S+NaI
- Ba3N2+H2O→Ba(OH)2+NH3
- CaCl2+Na3PO4→Ca3(PO4)2+NaCl
In the section on dimensionless variables it was observed that ρV2AB has the units of force. Describe a systematic way to obtain such combinations of the variables which will yield something which has the units of force.
Consider the following diagram of four circuits.
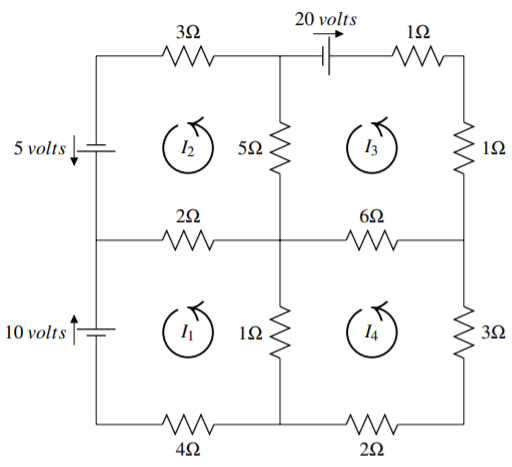
The current in amps in the four circuits is denoted by I1,I2,I3,I4 and it is understood that the motion is in the counter clockwise direction. If Ik ends up being negative, then it just means the current flows in the clockwise direction.
In the above diagram, the top left circuit should give the equation 2I2−2I1+5I2−5I3+3I2=5 For the circuit on the lower left, you should have 4I1+I1−I4+2I1−2I2=−10 Write equations for each of the other two circuits and then give a solution to the resulting system of equations.
- Answer
-
The other two equations are 6I3−6I4+I3+I3+5I3−5I2=−202I4+3I4+6I4−6I3+I4−I1=0 Then the system is 2I2−2I1+5I2−5I3+3I2=54I1+I1−I4+2I1−2I2=−106I3−6I4+I3+I3+5I3−5I2=−202I4+3I4+6I4−6I3+I4−I1=0 The solution is: I1=−750373I2=−14211119I3=−30611119I4=−17181119
Consider the following diagram of three circuits.
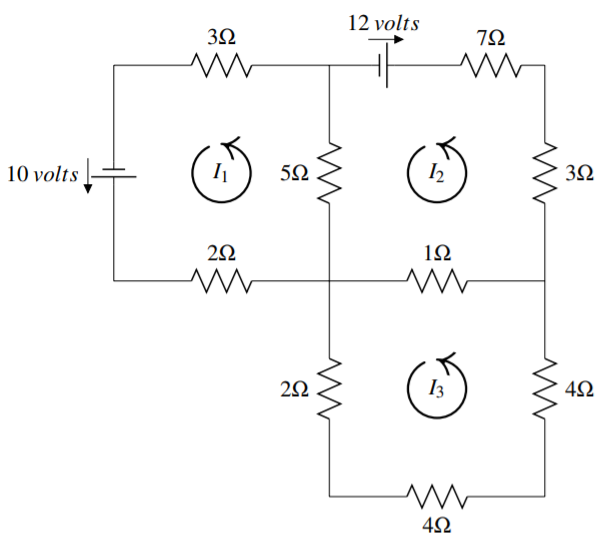
The current in amps in the four circuits is denoted by I1,I2,I3 and it is understood that the motion is in the counter clockwise direction. If Ik ends up being negative, then it just means the current flows in the clockwise direction.
Find I1,I2,I3.
- Answer
-
You have 2I1+5I1+3I1−5I2=10I2−I3+3I2+7I2+5I2−5I1=−122I3+4I3+4I3+I3−I2=0 Simplifying this yields 10I1−5I2=10−5I1+16I2−I3=−12−I2+11I3=0 The solution is given by I1=218295,I2=−154295,I3=−14295


