4.12: Applications

Applications

Outcomes

1. Apply the concepts of vectors in \(\mathbb{R}^n\) to the applications of physics and work.

Vectors and Physics

Suppose you push on something. Then, your push is made up of two components, how hard you push and the direction you push. This illustrates the concept of force.

Definition \(\PageIndex{1}\): Force

Force is a vector. The magnitude of this vector is a measure of how hard it is pushing. It is measured in units such as Newtons or pounds or tons. The direction of this vector is the direction in which the push is taking place.

Vectors are used to model force and other physical vectors like velocity. As with all vectors, a vector modeling force has two essential ingredients, its magnitude and its direction.

Recall the special vectors which point along the coordinate axes. These are given by \[\vec{e}_{i} = \left [ 0 \cdots 0 \; 1 \; 0 \cdots 0 \right ]^T\nonumber \] where the \(1\) is in the \(i^{th}\) slot and there are zeros in all the other spaces. The direction of \(\vec{e}_{i}\) is referred to as the \(i^{th}\) direction.

Consider the following picture which illustrates the case of \(\mathbb{R}^{3}.\) Recall that in \(\mathbb{R}^3\), we may refer to these vectors as \(\vec{i}, \vec{j},\) and \(\vec{k}\).

Figure \(\PageIndex{1}\)

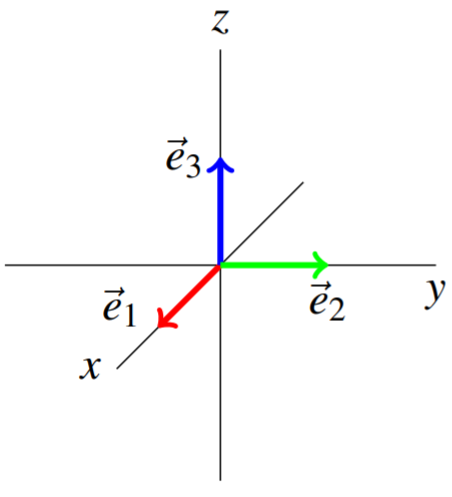
Given a vector \(\vec{u}=\left [ u_{1} \cdots u_{n}\right ]^T ,\) it follows that \[\vec{u}=u_{1}\vec{e}_{1}+\cdots +u_{n}\vec{e}_{n}= \sum_{k=1}^{n}u_{i}\vec{e}_{i}\nonumber \]

What does addition of vectors mean physically? Suppose two forces are applied to some object. Each of these would be represented by a force vector and the two forces acting together would yield an overall force acting on the object which would also be a force vector known as the resultant. Suppose the two vectors are \(\vec{u}=\sum_{k=1}^{n}u_{i}\vec{e}_{i}\) and \(\vec{v}=\sum_{k=1}^{n}v_{i}\vec{e}_{i}\). Then the vector \(\vec{u}\) involves a component in the \(i^{th}\) direction given by \(u_{i}\vec{e}_{i}\), while the component in the \(i^{th}\) direction of \(\vec{v}\) is \(v_{i}\vec{e}_{i}.\) Then the vector \(\vec{u} + \vec{v}\) should have a component in the \(i^{th}\) direction equal to \(\left( u_{i}+v_{i}\right) \vec{e}_{i}.\) This is exactly what is obtained when the vectors, \(\vec{u}\) and \(\vec{v}\) are added. \[\begin{aligned} \vec{u}+\vec{v}& =\left [ u_{1}+v_{1} \cdots u_{n}+v_{n}\right ]^T \\ & =\sum_{i=1}^{n}\left( u_{i}+v_{i}\right) \vec{e}_{i}\end{aligned}\]

Thus the addition of vectors according to the rules of addition in \(\mathbb{R }^{n}\) which were presented earlier, yields the appropriate vector which duplicates the cumulative effect of all the vectors in the sum.

Consider now some examples of vector addition.

Example \(\PageIndex{1}\): The Resultant of Three Forces

There are three ropes attached to a car and three people pull on these ropes. The first exerts a force of \(\vec{F}_1 = 2\vec{i} + 3\vec{j} -2 \vec{k}\) Newtons, the second exerts a force of \(\vec{F}_2 = 3\vec{i}+5\vec{j}+\vec{k}\) Newtons and the third exerts a force of \(5\vec{i}-\vec{j}+2\vec{k}\) Newtons. Find the total force in the direction of \(\vec{i}\).

Solution

To find the total force, we add the vectors as described above. This is given by \[\begin{aligned} &(2\vec{i}+3\vec{j}-2\vec{k}) + (3\vec{i}+5\vec{j}+\vec{k}) + (5\vec{i}-\vec{j}+2\vec{k})\\ &= (2 + 3 + 5) \vec{i} + (3 + 5 + -1) \vec{j} + (-2+1+2) \vec{k} \\ &= 10 \vec{i} + 7 \vec{j} + \vec{k}\end{aligned}\] Hence, the total force is \(10\vec{i}+7\vec{j}+\vec{k}\) Newtons. Therefore, the force in the \(\vec{i}\) direction is \(10\) Newtons.

Consider another example.

Example \(\PageIndex{2}\): Finding a Vector from Geometric Description

An airplane flies North East at 100 miles per hour. Write this as a vector.

Solution

A picture of this situation follows.

Figure \(\PageIndex{2}\)

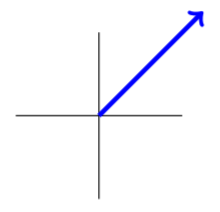
Therefore, we need to find the vector \(\vec{u}\) which has length 100 and direction as shown in this diagram. We can consider the vector \(\vec{u}\) as the hypotenuse of a right triangle having equal sides, since the direction of \(\vec{u}\) corresponds with the \(45 ^{\circ}\) line. The sides, corresponding to the \(\vec{i}\) and \(\vec{j}\) directions, should be each of length 100/\(\sqrt{2}.\) Therefore, the vector is given by \[\vec{u} = \frac{100}{\sqrt{2}} \vec{i}+ \frac{100}{\sqrt{2 }}\vec{j} = \left [ \begin{array}{rr} {0.05in} \frac{100}{\sqrt{2}} & {0.05in}\frac{100}{\sqrt{2}} \end{array} \right ]^T \nonumber \]

This example also motivates the concept of velocity, defined below.

Definition \(\PageIndex{2}\): Speed and Velocity

The speed of an object is a measure of how fast it is going. It is measured in units of length per unit time. For example, miles per hour, kilometers per minute, feet per second. The velocity is a vector having the speed as the magnitude but also specifying the direction.

Thus the velocity vector in the above example is \( {0.05in}\frac{100}{\sqrt{2}}\vec{i}+ {0.05in}\frac{100}{\sqrt{2}}\vec{j}\), while the speed is \(100\) miles per hour.

Consider the following example.

The velocity of an airplane is \(100\vec{i}+\vec{j}+\vec{k}\) measured in kilometers per hour and at a certain instant of time its position is \(\left( 1,2,1\right) .\)

Find the position of this airplane one minute later.

Solution

Here imagine a Cartesian coordinate system in which the third component is altitude and the first and second components are measured on a line from West to East and a line from South to North.

Consider the vector \(\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T ,\) which is the initial position vector of the airplane. As the plane moves, the position vector changes according to the velocity vector. After one minute (considered as \(\frac{1}{60}\) of an hour) the airplane has moved in the \(\vec{i}\) direction a distance of \(100\times \frac{1}{60}= \frac{5}{3}\) kilometer. In the \(\vec{j}\) direction it has moved \(\frac{1}{60}\) kilometer during this same time, while it moves \(\frac{1}{60}\) kilometer in the \(\vec{k}\) direction. Therefore, the new displacement vector for the airplane is \[\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T + \left [ \begin{array}{rrr} \frac{5}{3} & \frac{1}{60} & \frac{1}{60} \end{array} \right ]^T =\left [ \begin{array}{rrr} \frac{8}{3} & \frac{121}{60} & \frac{121}{60} \end{array} \right ]^T\nonumber \]

Now consider an example which involves combining two velocities.

Example \(\PageIndex{4}\): Sum of Two Velocities

A certain river is one half kilometer wide with a current flowing at 4 kilometers per hour from East to West. A man swims directly toward the opposite shore from the South bank of the river at a speed of 3 kilometers per hour. How far down the river does he find himself when he has swam across? How far does he end up swimming?

Solution

Consider the following picture which demonstrates the above scenario.

Figure \(\PageIndex{3}\)

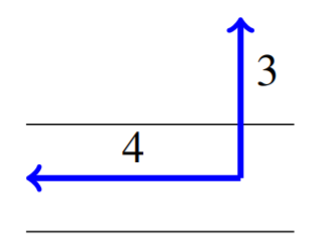
First we want to know the total time of the swim across the river. The velocity in the direction across the river is \(3\) kilometers per hour, and the river is \(\frac{1}{2}\) kilometer wide. It follows the trip takes \(1/6\) hour or \(10\) minutes.

Now, we can compute how far downstream he will end up. Since the river runs at a rate of \(4\) kilometers per hour, and the trip takes \(1/6\) hour, the distance traveled downstream is given by \(4 \left(\frac{1}{6}\right) = \frac{2}{3}\) kilometers.

The distance traveled by the swimmer is given by the hypotenuse of a right triangle. The two arms of the triangle are given by the distance across the river, \(\frac{1}{2}\)km, and the distance traveled downstream, \(\frac{2}{3}\) km. Then, using the Pythagorean Theorem, we can calculate the total distance \(d\) traveled. \[d = \sqrt{ \left(\frac{2}{3} \right)^2 + \left( \frac{1}{2} \right) ^2 } = \frac{5}{6} \mbox{km}\nonumber \]

Therefore, the swimmer travels a total distance of \(\frac{5}{6}\) kilometers.

Work

The mathematical concept of work is an application of vectors in \(\mathbb{R}^n\). The physical concept of work differs from the notion of work employed in ordinary conversation. For example, suppose you were to slide a 150 pound weight off a table which is three feet high and shuffle along the floor for 50 yards, keeping the height always three feet and then deposit this weight on another three foot high table. The physical concept of work would indicate that the force exerted by your arms did no work during this project. The reason for this definition is that even though your arms exerted considerable force on the weight, the direction of motion was at right angles to the force they exerted. The only part of a force which does work in the sense of physics is the component of the force in the direction of motion.

Work is defined to be the magnitude of the component of this force times the distance over which it acts, when the component of force points in the direction of motion. In the case where the force points in exactly the opposite direction of motion work is given by \(\left( -1\right)\) times the magnitude of this component times the distance. Thus the work done by a force on an object as the object moves from one point to another is a measure of the extent to which the force contributes to the motion. This is illustrated in the following picture in the case where the given force contributes to the motion.

Figure \(\PageIndex{4}\)

Recall that for any vector \(\vec{u}\) in \(\mathbb{R}^n\), we can write \(\vec{u}\) as a sum of two vectors, as in \[\vec{u} = \vec{u}_{||} + \vec{u}_{\perp}\nonumber \] For any force \(\vec{F}\), we can write this force as the sum of a vector in the direction of the motion and a vector perpendicular to the motion. In other words, \[\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\nonumber \]

In the above picture the force, \(\vec{F}\) is applied to an object which moves on the straight line from \(P\) to \(Q.\) There are two vectors shown, \(\vec{F}_{||}\) and \(\vec{F}_{\bot }\) and the picture is intended to indicate that when you add these two vectors you get \(\vec{F}\). In other words, \(\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\). Notice that \(\vec{F}_{||}\) acts in the direction of motion and \(\vec{F}_{\bot }\) acts perpendicular to the direction of motion. Only \(\vec{F}_{||}\) contributes to the work done by \(\vec{F}\) on the object as it moves from \(P\) to \(Q\). \(\vec{F}_{||}\) is called the component of the force in the direction of motion. From trigonometry, you see the magnitude of \(\vec{F}_{||}\) should equal \( \| \vec{F} \| \left| \cos \theta \right| .\) Thus, since \(\vec{F}_{||}\) points in the direction of the vector from \(P\) to \(Q,\) the total work done should equal \[ \| \vec{F} \| \| \vec{PQ} \| \cos \theta = \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta\nonumber \]

Now, suppose the included angle had been obtuse. Then the work done by the force \(\vec{F}\) on the object would have been negative because \(\vec{F}_{||}\) would point in \(-1\) times the direction of the motion. In this case, \(\cos \theta\) would also be negative and so it is still the case that the work done would be given by the above formula. Thus from the geometric description of the dot product given above, the work equals \[ \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta =\vec{F}\bullet \left( \vec{q}-\vec{p}\right)\nonumber \] This explains the following definition.

Definition \(\PageIndex{3}\): Work Done on an Object by a Force

Let \(\vec{F}\) be a force acting on an object which moves from the point \(P\) to the point \(Q\), which have position vectors given by \(\vec{p}\) and \(\vec{q}\) respectively. Then the work done on the object by the given force equals \(\vec{F}\bullet \left( \vec{q}-\vec{p}\right) .\)

Consider the following example.

Example \(\PageIndex{4}\): Finding Work

Let \(\vec{F}= \left [ \begin{array}{rrr} 2 & 7 & -3 \end{array} \right ]^T\) Newtons. Find the work done by this force in moving from the point \(\left( 1,2,3\right)\) to the point \(\left( -9,-3,4\right)\) along the straight line segment joining these points where distances are measured in meters.

Solution

First, compute the vector \(\vec{q} - \vec{p}\), given by \[\left [ \begin{array}{rrr} -9 & -3 & 4 \end{array} \right ]^T - \left [ \begin{array}{rrr} 1 & 2 & 3 \end{array} \right ]^T = \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T\nonumber \]

According to Definition \(\PageIndex{3}\) the work done is \[\begin{aligned} \left [ \begin{array}{rrr} 2 & 7 & 3 \end{array} \right ]^T \bullet \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T & =-20+\left( -35\right) +\left( -3\right) \\ & =-58\text{ Newton meters}\end{aligned}\]

Note that if the force had been given in pounds and the distance had been given in feet, the units on the work would have been foot pounds. In general, work has units equal to units of a force times units of a length. Recall that \(1\) Newton meter is equal to \(1\) Joule. Also notice that the work done by the force can be negative as in the above example.