8.2: Spherical and Cylindrical Coordinates
- Page ID
- 14546
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Understand cylindrical and spherical coordinates.
- Convert points between Cartesian, cylindrical, and spherical coordinates.
Spherical and cylindrical coordinates are two generalizations of polar coordinates to three dimensions. We will first look at cylindrical coordinates .
When moving from polar coordinates in two dimensions to cylindrical coordinates in three dimensions, we use the polar coordinates in the \(xy\) plane and add a \(z\) coordinate. For this reason, we use the notation \((r, \theta, z)\) to express cylindrical coordinates. The relationship between Cartesian coordinates \((x,y,z)\) and cylindrical coordinates \((r, \theta, z)\) is given by \[\begin{aligned} x& =r\cos \left( \theta \right) \\ y& =r\sin \left( \theta \right) \\ z& =z\end{aligned}\] where \(r\geq 0\), \(\theta \in \lbrack 0,2\pi ),\) and \(z\) is simply the Cartesian coordinate. Notice that \(x\) and \(y\) are defined as the usual polar coordinates in the \(xy\)-plane. Recall that \(r\) is defined as the length of the ray from the origin to the point \((x,y,0)\), while \(\theta\) is the angle between the positive \(x\)-axis and this same ray.
To illustrate this coordinate system, consider the following two pictures. In the first of these, both \(r\) and \(z\) are known. The cylinder corresponds to a given value for \(r\). A useful way to think of \(r\) is as the distance between a point in three dimensions and the \(z\)-axis. Every point on the cylinder shown is at the same distance from the \(z\)-axis. Giving a value for \(z\) results in a horizontal circle, or cross section of the cylinder at the given height on the \(z\) axis (shown below as a black line on the cylinder). In the second picture, the point is specified completely by also knowing \(\theta\) as shown.
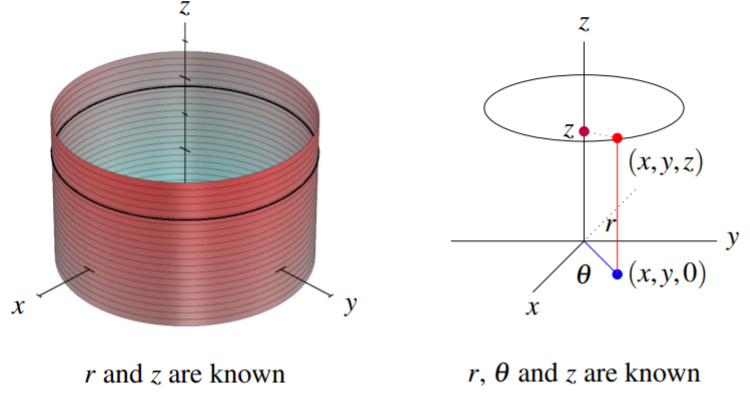
Every point of three dimensional space other than the \(z\) axis has unique cylindrical coordinates. Of course there are infinitely many cylindrical coordinates for the origin and for the \(z\)-axis. Any \(\theta\) will work if \(r=0\) and \(z\) is given.
Consider now spherical coordinates, the second generalization of polar form in three dimensions. For a point \((x,y,z)\) in three dimensional space, the spherical coordinates are defined as follows. \[\begin{array}{l} \rho: \mbox{the length of the ray from the origin to the point}\\ \theta: \mbox{the angle between the positive $x$-axis and the ray from the origin to the point $(x,y,0)$}\\ \phi: \mbox{the angle between the positive $z$-axis and the ray from the origin to the point of interest} \end{array}\nonumber \] The spherical coordinates are determined by \(\left( \rho ,\phi ,\theta \right)\). The relation between these and the Cartesian coordinates \(\left( x,y,z \right)\) for a point are as follows. \[\begin{aligned} x& =\rho \sin \left( \phi \right) \cos \left( \theta \right) ,\ \phi \in \left[ 0,\pi \right] \\ y& =\rho \sin \left( \phi \right) \sin \left( \theta \right) ,\text{ }\theta \in \lbrack 0,2\pi ) \\ z& =\rho \cos \phi \text{, }\rho \geq 0.\end{aligned}\]
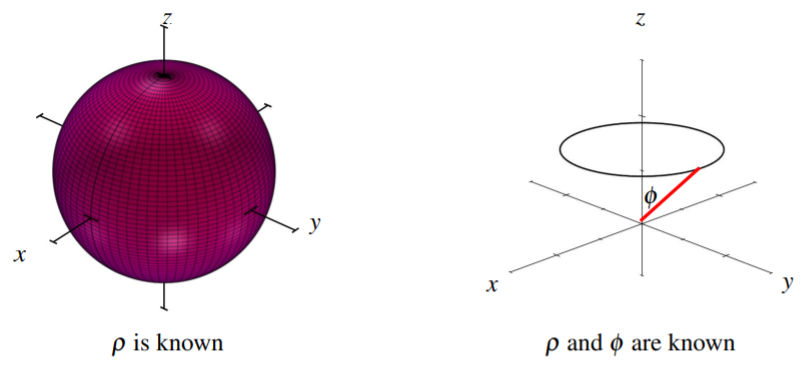
Consider the pictures below. The first illustrates the surface when \(\rho\) is known, which is a sphere of radius \(\rho\). The second picture corresponds to knowing both \(\rho\) and \(\phi\), which results in a circle about the \(z\)-axis. Suppose the first picture demonstrates a graph of the Earth. Then the circle in the second picture would correspond to a particular latitude.
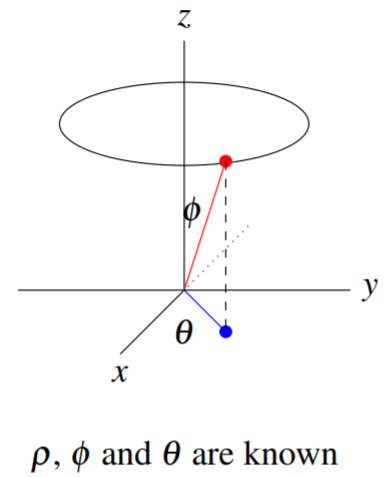
Giving the third coordinate, \(\theta\) completely specifies the point of interest. This is demonstrated in the following picture. If the latitude corresponds to \(\phi\), then we can think of \(\theta\) as the longitude.
The following picture summarizes the geometric meaning of the three coordinate systems.
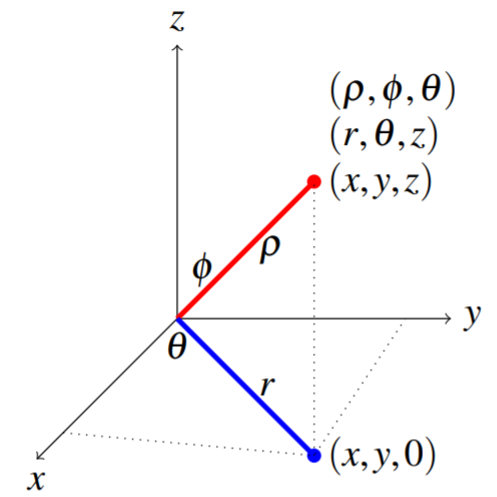
Therefore, we can represent the same point in three ways, using Cartesian coordinates, \(\left(x,y,z\right)\), cylindrical coordinates, \(\left( r, \theta, z \right)\), and spherical coordinates \(\left( \rho, \phi, \theta \right)\).
Using this picture to review, call the point of interest \(P\) for convenience. The Cartesian coordinates for \(P\) are \((x,y,z)\). Then \(\rho\) is the distance between the origin and the point \(P\). The angle between the positive \(z\) axis and the line between the origin and \(P\) is denoted by \(\phi\). Then \(\theta\) is the angle between the positive \(x\) axis and the line joining the origin to the point \(\left( x,y,0\right)\) as shown. This gives the spherical coordinates, \(( \rho, \phi, \theta)\). Given the line from the origin to \(\left( x,y,0\right)\), \(r=\rho \sin(\phi)\) is the length of this line. Thus \(r\) and \(\theta\) determine a point in the \(xy\)-plane. In other words, \(r\) and \(\theta\) are the usual polar coordinates and \(r\geq 0\) and \(\theta \in \lbrack 0,2\pi )\). Letting \(z\) denote the usual \(z\) coordinate of a point in three dimensions, \(\left( r,\theta ,z\right)\) are the cylindrical coordinates of \(P\).
The relation between spherical and cylindrical coordinates is that \(r=\rho \sin(\phi)\) and the \(\theta\) is the same as the \(\theta\) of cylindrical and polar coordinates.
We will now consider some examples.
Express the surface \(z=\frac{1}{\sqrt{3}}\sqrt{x^{2}+y^{2}}\) in spherical coordinates.
Solution
We will use the equations from above: \[\begin{array}{l} x =\rho \sin \left( \phi \right) \cos \left( \theta \right), \phi \in \left[ 0,\pi \right]\\ y =\rho \sin \left( \phi \right) \sin \left( \theta \right) ,\text{ }\theta \in \lbrack 0,2\pi ) \\ z =\rho \cos \phi \text{, }\rho \geq 0 \end{array} \nonumber\]
To express the surface in spherical coordinates, we substitute these expressions into the equation. This is done as follows:
\[\rho \cos \left( \phi \right) =\frac{1}{\sqrt{3}}\sqrt{\left( \rho \sin \left( \phi \right) \cos \left( \theta \right) \right) ^{2}+\left( \rho \sin \left( \phi \right) \sin \left( \theta \right) \right) ^{2}}= \frac{1}{3}\sqrt{3}\rho \sin \left( \phi \right). \nonumber\]
This reduces to \[\tan \left( \phi \right)=\sqrt{3} \nonumber\] and so \(\phi =\pi /3\).
Express the surface \(y=x\) in terms of spherical coordinates.
Solution
Using the same procedure as the previous example, this says \( \rho \sin \left( \phi \right) \sin \left( \theta \right) =\rho \sin \left( \phi \right) \cos \left( \theta \right)\). Simplifying, \(\sin \left( \theta \right) =\cos \left( \theta \right)\), which you could also write \(\tan \left( \theta \right)=1\).
We conclude this section with an example of how to describe a surface using cylindrical coordinates.
Express the surface \(x^{2}+y^{2}=4\) in cylindrical coordinates.
Solution
Recall that to convert from Cartesian to cylindrical coordinates, we can use the following equations: \[x =r\cos \left( \theta \right) , y=r\sin \left( \theta \right) , z =z\nonumber \]
Substituting these equations in for \(x,y,z\) in the equation for the surface, we have \[r^{2}\cos ^{2} \left( \theta \right) +r^{2}\sin ^{2} \left( \theta \right)=4\nonumber \] This can be written as \(r^2 ( \cos^{2} \left( \theta \right)+ \sin^{2} \left(\theta\right) ) = 4\). Recall that \(\cos^{2} \left( \theta \right)+ \sin^{2} \left( \theta \right)=1\). Thus \(r^{2} = 4\) or \(r=2\).


