1.1: Systems of Equations, Geometry
( \newcommand{\kernel}{\mathrm{null}\,}\)
Systems of Equations, Geometry
- Relate the types of solution sets of a system of two (three) variables to the intersections of lines in a plane (the intersection of planes in three space)
As you may remember, linear equations like 2x+3y=6 can be graphed as straight lines in the coordinate plane. We say that this equation is in two variables, in this case x and y. Suppose you have two such equations, each of which can be graphed as a straight line, and consider the resulting graph of two lines. What would it mean if there exists a point of intersection between the two lines? This point, which lies on both graphs, gives x and y values for which both equations are true. In other words, this point gives the ordered pair (x,y) that satisfy both equations. If the point (x,y) is a point of intersection, we say that (x,y) is a solution to the two equations. In linear algebra, we often are concerned with finding the solution(s) to a system of equations, if such solutions exist. First, we consider graphical representations of solutions and later we will consider the algebraic methods for finding solutions.
When looking for the intersection of two lines in a graph, several situations may arise. The following picture demonstrates the possible situations when considering two equations (two lines in the graph) involving two variables.
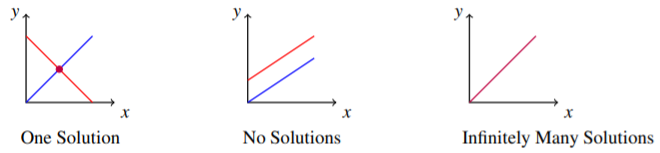
In the first diagram, there is a unique point of intersection, which means that there is only one (unique) solution to the two equations. In the second, there are no points of intersection and no solution. When no solution exists, this means that the two lines are parallel and they never intersect. The third situation which can occur, as demonstrated in diagram three, is that the two lines are really the same line. For example, x+y=1 and 2x+2y=2 are equations which when graphed yield the same line. In this case there are infinitely many points which are solutions of these two equations, as every ordered pair which is on the graph of the line satisfies both equations. When considering linear systems of equations, there are always three types of solutions possible; exactly one (unique) solution, infinitely many solutions, or no solution.
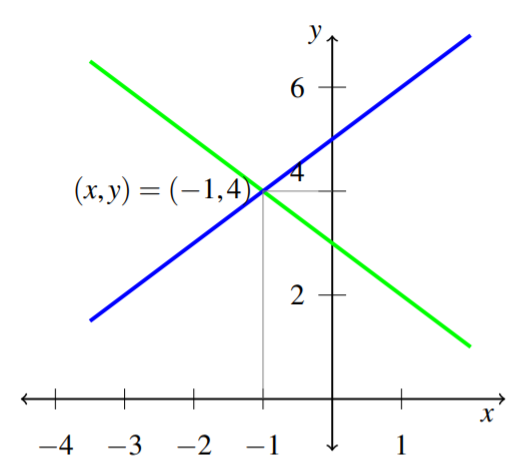
Use a graph to find the solution to the following system of equations x+y=3y−x=5
Solution
Through graphing the above equations and identifying the point of intersection, we can find the solution(s). Remember that we must have either one solution, infinitely many, or no solutions at all. The following graph shows the two equations, as well as the intersection. Remember, the point of intersection represents the solution of the two equations, or the (x,y) which satisfy both equations. In this case, there is one point of intersection at (−1,4) which means we have one unique solution, x=−1,y=4.
In the above example, we investigated the intersection point of two equations in two variables, x and y. Now we will consider the graphical solutions of three equations in two variables.
Consider a system of three equations in two variables. Again, these equations can be graphed as straight lines in the plane, so that the resulting graph contains three straight lines. Recall the three possible types of solutions; no solution, one solution, and infinitely many solutions. There are now more complex ways of achieving these situations, due to the presence of the third line. For example, you can imagine the case of three intersecting lines having no common point of intersection. Perhaps you can also imagine three intersecting lines which do intersect at a single point. These two situations are illustrated below.
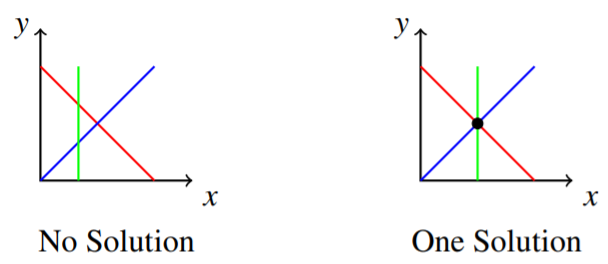
Consider the first picture above. While all three lines intersect with one another, there is no common point of intersection where all three lines meet at one point. Hence, there is no solution to the three equations. Remember, a solution is a point (x,y) which satisfies all three equations. In the case of the second picture, the lines intersect at a common point. This means that there is one solution to the three equations whose graphs are the given lines. You should take a moment now to draw the graph of a system which results in three parallel lines. Next, try the graph of three identical lines. Which type of solution is represented in each of these graphs?
We have now considered the graphical solutions of systems of two equations in two variables, as well as three equations in two variables. However, there is no reason to limit our investigation to equations in two variables. We will now consider equations in three variables.
You may recall that equations in three variables, such as 2x+4y−5z=8, form a plane. Above, we were looking for intersections of lines in order to identify any possible solutions. When graphically solving systems of equations in three variables, we look for intersections of planes. These points of intersection give the (x,y,z) that satisfy all the equations in the system. What types of solutions are possible when working with three variables? Consider the following picture involving two planes, which are given by two equations in three variables.
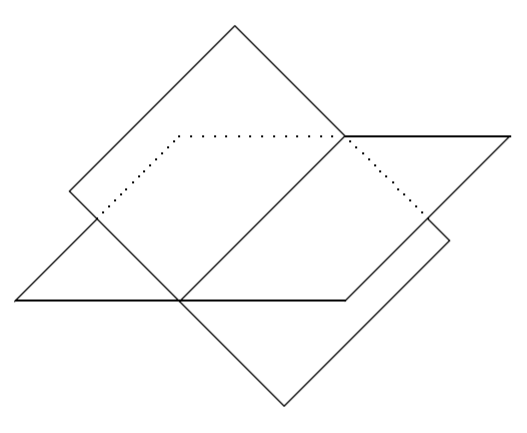
Notice how these two planes intersect in a line. This means that the points (x,y,z) on this line satisfy both equations in the system. Since the line contains infinitely many points, this system has infinitely many solutions.
It could also happen that the two planes fail to intersect. However, is it possible to have two planes intersect at a single point? Take a moment to attempt drawing this situation, and convince yourself that it is not possible! This means that when we have only two equations in three variables, there is no way to have a unique solution! Hence, the types of solutions possible for two equations in three variables are no solution or infinitely many solutions.
Now imagine adding a third plane. In other words, consider three equations in three variables. What types of solutions are now possible? Consider the following diagram.
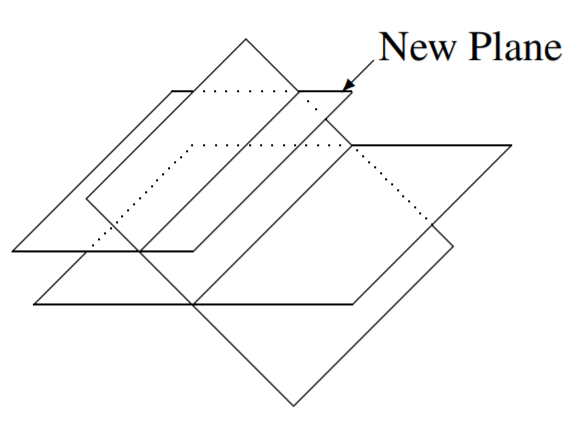
In this diagram, there is no point which lies in all three planes. There is no intersection between all planes so there is no solution. The picture illustrates the situation in which the line of intersection of the new plane with one of the original planes forms a line parallel to the line of intersection of the first two planes. However, in three dimensions, it is possible for two lines to fail to intersect even though they are not parallel. Such lines are called skew lines.
Recall that when working with two equations in three variables, it was not possible to have a unique solution. Is it possible when considering three equations in three variables? In fact, it is possible, and we demonstrate this situation in the following picture.
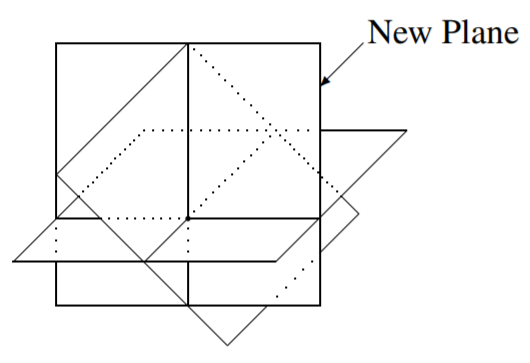
In this case, the three planes have a single point of intersection. Can you think of other types of solutions possible? Another is that the three planes could intersect in a line, resulting in infinitely many solutions, as in the following diagram.
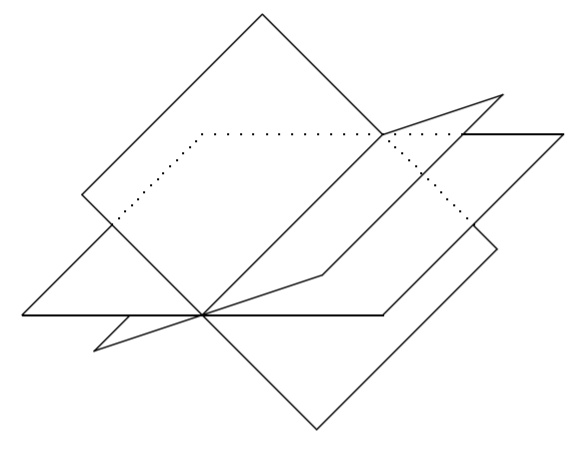
We have now seen how three equations in three variables can have no solution, a unique solution, or intersect in a line resulting in infinitely many solutions. It is also possible that the three equations graph the same plane, which also leads to infinitely many solutions.
You can see that when working with equations in three variables, there are many more ways to achieve the different types of solutions than when working with two variables. It may prove enlightening to spend time imagining (and drawing) many possible scenarios, and you should take some time to try a few.
You should also take some time to imagine (and draw) graphs of systems in more than three variables. Equations like x+y−2z+4w=8 with more than three variables are often called hyper-planes. You may soon realize that it is tricky to draw the graphs of hyper-planes! Through the tools of linear algebra, we can algebraically examine these types of systems which are difficult to graph. In the following section, we will consider these algebraic tools.
Graphically, find the point (x1,y1) which lies on both lines, x+3y=1 and 4x−y=3. That is, graph each line and see where they intersect.
Graphically, find the point of intersection of the two lines, 3x+y=3 and x+2y=1. That is, graph each line and see where they intersect
You have a system of k equations in two variables, k≥2. Explain the geometric significance of
- No solution.
- A unique solution.
- An infinite number of solutions.


