4.4: Sums and direct sum
- Page ID
- 317
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Throughout this section, \(V\) is a vector space over \(\mathbb{F}\), and \(U_1 , U_2 \subset V\) denote subspaces.
Definition 4.4.1: (subspace) sum
Let \(U_1 , U_2 \subset V\) be subspaces of \(V\) . Define the (subspace) sum of \(U_1\)
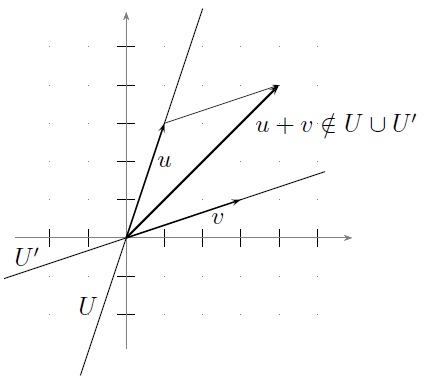
Figure 4.4.1: The union \(U \cup U^\prime\) of two subspaces is not necessarily a subspace.
and \(U_2\) to be the set
\[ U_1 + U_2 = \{u_1 + u_2 | u_1 \in U_1 , u_2 \in U_2 \}. \tag{4.4.1}\]
Check as an exercise that \(U_1 + U_2\) is a subspace of \(V\) . In fact, \(U_1 + U_2\) is the smallest subspace of \(V\) that contains both \(U_1\) and \(U_2\) .
Example 4.4.2. Let
\[ U_1 = \{(x, 0, 0) \in \mathbb{F}^3 | x \in \mathbb{F}\}, \\ U_2 = \{(0, y, 0) \in \mathbb{F}^3 | y \in \mathbb{F}\}.\]
Then
\[U_1 + U_2 = \{(x, y, 0) \in \mathbb{F}^3 | x, y \in \mathbb{F}\}. \tag{4.4.2}\]
If, alternatively, \(U_2 = \{(y, y, 0) \in \mathbb{F}^3 | y \in \mathbb{F}\}\), then Equation (4.4.2) still holds.
If \(U = U_1 +U_2\) , then, for any \(u \in U\), there exist \(u_1 \in U_1\) and \(u_2 \in U_2\) such that \(u = u_1 +u_2.\)
If it so happens that \(u\) can be uniquely written as \(u_1 + u_2\) , then \(U\) is called the direct sum of \(U_1\) and \(U_2.\)
Definition 4.4.3: Direct Sum
Suppose every \(u \in U\) can be uniquely written as \(u = u_1 + u_2\) for \( u_1 \in U_1\) and \(u_2 \in U_2\) . Then we use
\[U = U_1 \oplus U_2\]
to denote the direct sum of \(U_1\) and \(U_2.\)
Example 4.4.4. Let
\[U_1 = \{(x, y, 0) \in \mathbb{R}^3 | x, y \in \mathbb{R}\}, \\
U_2 = \{(0, 0, z) \in \mathbb{R}^3 | z \in \mathbb{R}\}.\]
Then \(\mathbb{R}^3 = U_1 \oplus U_2\). However, if instead
\[U_2 = \{(0, w, z) | w, z \in \mathbb{R}\},\]
then \(\mathbb{R}^3 = U_1 + U_2\) but is not the direct sum of \(U_1\) and \(U_2\) .
Example 4.4.5. Let
\[U_1 = \{p \in \mathbb{F}[z] | p(z) = a_0 + a_2 z^2 + \cdots + a_{2m}z^{2m} \}, \\
U_2 = \{p \in \mathbb{F}[z] | p(z) = a_1z + a_3z^3 + \cdots + a_{2m+1}z^{2m+1} \}.\]
Then \(\mathbb{F}[z] = U_1 \oplus U_2.\)
Proposition 4.4.6. Let \(U_1 , U_2 \subset V\) be subspaces. Then \(V = U_1 \oplus U_2\) if and only if the following two conditions hold:
- \(V = U_1 + U_2;\)
- If \(0 = u_1 + u_2\) with \(u_1 \in U_1\) and \(u_2 \in U_2\) , then \(u_1 = u_2 = 0.\)
Proof.
\((“\Rightarrow”)\) Suppose \(V = U_1 \oplus U_2\). Then Condition 1 holds by definition. Certainly \(0 = 0 + 0\), and, since by uniqueness this is the only way to write \(0 \in V\) , we have \(u_1 = u_2 = 0\).
\((“\Leftarrow”)\) Suppose Conditions 1 and 2 hold. By Condition 1, we have that, for all \(v \in V\) , there exist \(u_1 \in U_1\) and \(u_2 \in U_2\) such that \(v = u_1 + u_2\) . Suppose \(v = w_1 + w_2\) with \(w_1 \in U_1\) and \(w_2 \in U_2\) . Subtracting the two equations, we obtain
\[0 = (u_1 − w_1 ) + (u_2 − w_2 ),\]
where \(u_1 − w_1 \in U_1\) and \(u_2 − w_2 \in U_2\). By Condition 2, this implies \(u_1 − w_1 = 0\) and \(u_2 − w_2 = 0\), or equivalently \(u_1 = w_1\) and \(u_2 = w_2\) , as desired.
Proposition 4.4.7. Let \(U_1 , U_2 \subset V\) be subspaces. Then \(V = U_1 \oplus U_2\) if and only if the following two conditions hold:
- \(V = U_1 + U_2;\)
- \(U_1 \cap U_2 = \{0\}.\)
Proof.
\((“\Rightarrow”)\) Suppose \(V = U_1 \oplus U_2\). Then Condition 1 holds by definition. If \(u \in U_1 \cap U_2\) , then \(0 = u + (−u)\) with \(u \in U_1\) and \(−u \in U_2\) (why?). By Proposition 4.4.6, we have \(u = 0\) and \(−u = 0\) so that \(U_1 \cap U_2 = \{0\}.\)
\((“\Leftarrow”)\) Suppose Conditions 1 and 2 hold. To prove that \(V = U_1 \oplus U_2\) holds, suppose that
\[0 = u_1 + u_2, \rm{~where~} u_1 \in U_1 \rm{~and~} u_2 \in U_2. \tag{4.3}\]
By Proposition 4.4.6, it suffices to show that \(u_1 = u_2 = 0\). Equation (4.3) implies that \(u_1 = −u_2 \in U_2\). Hence \(u_1 \in U_1 \cap U_2\), which in turn implies that \(u_1 = 0\). It then follows that \(u_2 = 0\) as well.
Everything in this section can be generalized to m subspaces \(U_1 , U_2 , \ldots U_m,\) with the notable exception of Proposition 4.4.7. To see, this consider the following example.
Example 4.4.8. Let
\[U_1 = \{(x, y, 0) \in \mathbb{F}^3 | x, y \in \mathbb{F}\}, \\
U_2 = \{(0, 0, z) \in \mathbb{F}^3 | z \in \mathbb{F}\}, \\
U_3 = \{(0, y, y) \in \mathbb{F}^3 | y \in \mathbb{F}\}.\]
Then certainly \(\mathbb{F}^3 = U_1 + U_2 + U_3\) , but \(\mathbb{F}^3 \neq U_1 \oplus U_2 \oplus U_3\) since, for example,
\[(0, 0, 0) = (0, 1, 0) + (0, 0, 1) + (0, −1, −1).\]
But \(U_1 \cap U_2 = U_1 \cap U_3 = U_2 \cap U_3 = \{0\}\) so that the analog of Proposition 4.4.7 does not hold.
Contributors
- Isaiah Lankham, Mathematics Department at UC Davis
- Bruno Nachtergaele, Mathematics Department at UC Davis
- Anne Schilling, Mathematics Department at UC Davis
Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.


