2.3.1: Exercises 2.3

Last updated
Save as PDF

Page ID: 65825

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In Exercises $\PageIndex{1}$ - $\PageIndex{4}$, vectors $\vec{x}$ and $\vec{y}$ are given. Sketch $\vec{x}$, $\vec{y}$, $\vec{x}+\vec{y}$, and $\vec{x}-\vec{y}$ on the same Cartesian axes.

Exercise $\PageIndex{1}$

$\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-2}\\{3}\end{array}\right]$

Answer

$\vec{x}+\vec{y}=\left[\begin{array}{c}{-1}\\{4}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{3}\\{-2}\end{array}\right]$

Sketches will vary depending on choice of origin of each vector.

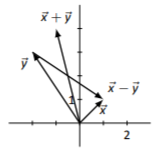
$clipboard_eb6afde601d93e3eecbf4c5e3b6d0fda8.png$

Figure $\PageIndex{1}$

Exercise $\PageIndex{2}$

$\vec{x}=\left[\begin{array}{c}{3}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{1}\\{-2}\end{array}\right]$

Answer

$\vec{x}+\vec{y}=\left[\begin{array}{c}{4}\\{-1}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{2}\\{3}\end{array}\right]$

Sketches will vary depending on choice of origin of each vector.

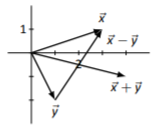
$clipboard_e50ab5c5fd94da72dd50ca5c4487ad15c.png$

Figure $\PageIndex{2}$

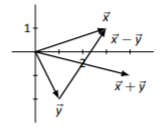
Exercise $\PageIndex{3}$

$\vec{x}=\left[\begin{array}{c}{-1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-2}\\{2}\end{array}\right]$

Answer

$\vec{x}+\vec{y}=\left[\begin{array}{c}{-3}\\{3}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{1}\\{-1}\end{array}\right]$

Sketches will vary depending on choice of origin of each vector.

$clipboard_e4be8d13f77b537ea8af36f89380ff0dc.png$

Figure $\PageIndex{3}$

Exercise $\PageIndex{4}$

$\vec{x}=\left[\begin{array}{c}{2}\\{0}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{1}\\{3}\end{array}\right]$

Answer

$\vec{x}+\vec{y}=\left[\begin{array}{c}{3}\\{3}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{1}\\{-3}\end{array}\right]$

Sketches will vary depending on choice of origin of each vector.

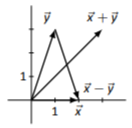
$clipboard_e881e342a01d3c4b9a6ba524bc3afe08d.png$

Figure $\PageIndex{4}$

In Exercises $\PageIndex{5}$ – $\PageIndex{8}$, vectors $\vec{x}$ and $\vec{y}$ are drawn. Sketch $2\vec{x}-\vec{y}$, $\vec{x}+\vec{y}$, $\vec{x}-\vec{y}$ on the same Cartesian axes.

Exercise $\PageIndex{5}$

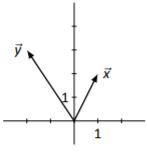
$clipboard_e9a1257242344e3758c7ae7d5a3d18842.png$

Figure $\PageIndex{5}$

Answer

Sketches will vary depending on choice of origin of each vector.

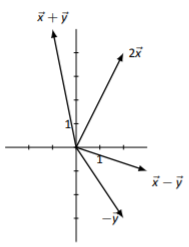
$clipboard_e28bc043d0c6546e81e4aa1e42c7344ee.png$

Figure $\PageIndex{6}$

Exercise $\PageIndex{6}$

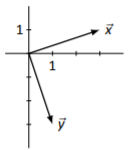
$clipboard_e4e9e6251b4dcf271e722d9ba64cabf3d.png$

Figure $\PageIndex{7}$

Answer

Sketches will vary depending on choice of origin of each vector.

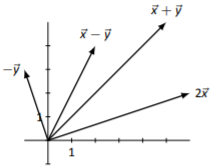
$clipboard_e40ca7a96320c26503bf70cd9f5a09640.png$

Figure $\PageIndex{8}$

Exercise $\PageIndex{7}$

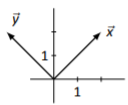
$clipboard_ef3c7212e26e117cbe4622858a2674fe6.png$

Figure $\PageIndex{9}$

Answer

Sketches will vary depending on choice of origin of each vector.

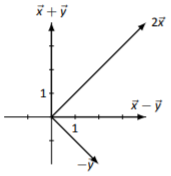
$clipboard_eca2094ba3146a48775d6b127166a8ccb.png$

Figure $\PageIndex{10}$

Exercise $\PageIndex{8}$

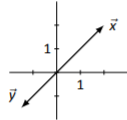
$clipboard_e54154257296c11a359cd4e3d9d469ad4.png$

Figure $\PageIndex{11}$

Answer

Sketches will vary depending on choice of origin of each vector.

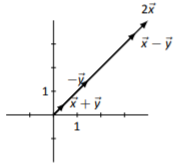
$clipboard_ef1e5163f7fabc779e9652408b895a6f6.png$

Figure $\PageIndex{12}$

In Exercises $\PageIndex{9}$ - $\PageIndex{12}$, a vector $\vec{x}$ and a scalar $a$ are given. Using Definition Vector Length compute the lengths of $\vec{x}$ and $a\vec{x}$, then compare these lengths.

Exercise $\PageIndex{9}$

$\vec{x}=\left[\begin{array}{c}{2}\\{1}\end{array}\right],\quad a=3$

Answer: $||\vec{x}||=\sqrt{5};\: ||a\vec{x}||=\sqrt{45}=3\sqrt{5}$. The vector $a\vec{x}$ is $3$ times as long as $\vec{x}$.

Exercise $\PageIndex{10}$

$\vec{x}=\left[\begin{array}{c}{4}\\{7}\end{array}\right],\quad a=-2$

Answer: $||\vec{x}||=\sqrt{65};\: ||a\vec{x}||=\sqrt{260}=2\sqrt{65}$. The vector $a\vec{x}$ is $2$ times as long as $\vec{x}$.

Exercise $\PageIndex{11}$

$\vec{x}=\left[\begin{array}{c}{-3}\\{5}\end{array}\right],\quad a=-1$

Answer: $||\vec{x}||=\sqrt{34};\: ||a\vec{x}||=\sqrt{34}$. The vectors $a\vec{x}$ and $\vec{x}$ are the same length (they just point in opposite directions).

Exercise $\PageIndex{12}$

$\vec{x}=\left[\begin{array}{c}{3}\\{-9}\end{array}\right],\quad a=\frac{1}{3}$

Answer: $||\vec{x}||=\sqrt{90}=3\sqrt{10};\: ||a\vec{x}||=\sqrt{10}$. The vector $a\vec{x}$ is one-third the length of $\vec{x}$; equivalently, $\vec{x}$ is $3$ times as long as $a\vec{x}$.

Exercise $\PageIndex{13}$

Four pairs of vectors $\vec{x}$ and $\vec{y}$ are given below. For each pair, compute $||\vec{x}||$, $||\vec{y}||$, and $||\vec{x}+\vec{y}||$. Use this information to answer: Is it always, sometimes, or never true that $||\vec{x}||+||\vec{y}||=||\vec{x}+\vec{y}||$? If it always or never true, explain why. If it is sometimes true, explain when it is true.

$\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{2}\\{3}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{1}\\{-2}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{3}\\{-6}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{-1}\\{3}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{2}\\{5}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{2}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-4}\\{-2}\end{array}\right]$

Answer

$||\vec{x}||=\sqrt{2};\: ||\vec{y}||=\sqrt{13};\: ||\vec{x}+\vec{y}||=5$.
$||\vec{x}||=\sqrt{5};\: ||\vec{y}||=3\sqrt{5};\: ||\vec{x}+\vec{y}||=4\sqrt{5}$.
$||\vec{x}||=\sqrt{10};\: ||\vec{y}||=\sqrt{29};\: ||\vec{x}+\vec{y}||=\sqrt{65}$.
$||\vec{x}||=\sqrt{5};\: ||\vec{y}||=2\sqrt{5};\: ||\vec{x}+\vec{y}||=\sqrt{5}$.

The equality holds sometimes; only when $\vec{x}$ and $\vec{y}$ point along the same line, in the same direction.

In Exercises $\PageIndex{14}$ - $\PageIndex{17}$, a matrix $A$ is given. Sketch $\vec{x}$, $\vec{y}$, $A\vec{x}$ and $A\vec{y}$ on the same Cartesian axes, where

\[\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right]\quad\text{and}\quad\vec{y}=\left[\begin{array}{c}{-1}\\{2}\end{array}\right]\nonumber \]

Exercise $\PageIndex{14}$

$A=\left[\begin{array}{cc}{1}&{-1}\\{2}&{3}\end{array}\right]$

Answer

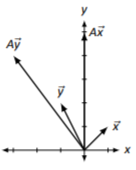
$clipboard_eb8b3bc5c904ff285e713c8b3d1d33e83.png$

Figure $\PageIndex{13}$

Exercise $\PageIndex{15}$

$A=\left[\begin{array}{cc}{2}&{0}\\{-1}&{3}\end{array}\right]$

Answer

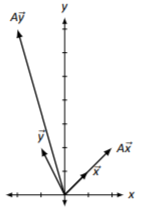
$clipboard_e7967cac33255a511639e33dcf7a32ae5.png$

Figure $\PageIndex{14}$

Exercise $\PageIndex{16}$

$A=\left[\begin{array}{cc}{1}&{1}\\{1}&{1}\end{array}\right]$

Answer

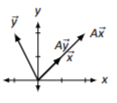
$clipboard_e219599a02a9c6f12a0bbd8ea542f9c04.png$

Figure $\PageIndex{15}$

Exercise $\PageIndex{17}$

$A=\left[\begin{array}{cc}{1}&{2}\\{-1}&{-2}\end{array}\right]$

Answer

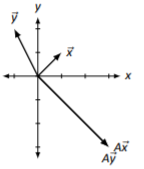
$clipboard_e90e6b48da32ca970fec11a418c19acf5.png$

Figure $\PageIndex{16}$

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)