Skip to main content
Mathematics LibreTexts

2.4.1: Exercises 2.4

  1. Last updated
  2. Save as PDF
  • Page ID
    67842

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    In Exercises \(\PageIndex{1}\) – \(\PageIndex{6}\), a matrix \(A\) and vectors \(\vec{b}\), \(\vec{u}\) and \(\vec{v}\) are given. Verify that \(\vec{u}\) and \(\vec{v}\) are both solutions to the equation \(A\vec{x}=\vec{b}\); that is, show that \(A\vec{u}=A\vec{v}=\vec{b}\).

    Exercise \(\PageIndex{1}\)

    \(A=\left[\begin{array}{cc}{1}&{-2}\\{-3}&{6}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{0}\\{0}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{2}\\{1}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{-10}\\{-5}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    Exercise \(\PageIndex{2}\)

    \(A=\left[\begin{array}{cc}{1}&{-2}\\{-3}&{6}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{2}\\{-6}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{0}\\{-1}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{2}\\{0}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    Exercise \(\PageIndex{3}\)

    \(A=\left[\begin{array}{cc}{1}&{0}\\{2}&{0}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{0}\\{0}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{0}\\{-1}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{0}\\{59}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    Exercise \(\PageIndex{4}\)

    \(A=\left[\begin{array}{cc}{1}&{0}\\{2}&{0}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{-3}\\{-6}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{-3}\\{-1}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{-3}\\{59}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    Exercise \(\PageIndex{5}\)

    \(A=\left[\begin{array}{cccc}{0}&{-3}&{-1}&{-3}\\{-4}&{2}&{-3}&{5}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{0}\\{0}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{11}\\{4}\\{-12}\\{0}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{9}\\{-12}\\{0}\\{12}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    Exercise \(\PageIndex{6}\)

    \(A=\left[\begin{array}{cccc}{0}&{-3}&{-1}&{-3}\\{-4}&{2}&{-3}&{5}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{48}\\{36}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{-17}\\{-16}\\{0}\\{0}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{-8}\\{-28}\\{0}\\{12}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\) and \(A\vec{v}\) to verify.

    In Exercises \(\PageIndex{7}\) - \(\PageIndex{9}\), a matrix \(A\) and vectors \(\vec{b}\), \(\vec{u}\) and \(\vec{v}\) are given. Verify that \(A\vec{u}=\vec{0}\), \(A\vec{v}=\vec{b}\) and \(A(\vec{u}+\vec{v})=\vec{b}\).

    Exercise \(\PageIndex{7}\)

    \(A=\left[\begin{array}{ccc}{2}&{-2}&{-1}\\{-1}&{1}&{-1}\\{-2}&{2}&{-1}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{1}\\{1}\\{1}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{1}\\{1}\\{0}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{1}\\{1}\\{-1}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\), \(A\vec{v}\) and \(A(\vec{u}+\vec{v})\) to verify.

    Exercise \(\PageIndex{8}\)

    \(A=\left[\begin{array}{ccc}{1}&{-1}&{3}\\{3}&{-3}&{-3}\\{-1}&{1}&{1}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{-1}\\{-3}\\{1}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{2}\\{2}\\{0}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{2}\\{3}\\{0}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\), \(A\vec{v}\) and \(A(\vec{u}+\vec{v})\) to verify.

    Exercise \(\PageIndex{9}\)

    \(A=\left[\begin{array}{ccc}{2}&{0}&{0}\\{0}&{1}&{-3}\\{3}&{1}&{-3}\end{array}\right],\)

    \(\vec{b}=\left[\begin{array}{c}{2}\\{-4}\\{-1}\end{array}\right],\:\vec{u}=\left[\begin{array}{c}{0}\\{6}\\{2}\end{array}\right],\:\vec{v}=\left[\begin{array}{c}{1}\\{-1}\\{1}\end{array}\right]\)

    Answer

    Multiply \(A\vec{u}\), \(A\vec{v}\) and \(A(\vec{u}+\vec{v})\) to verify.

    In Exercises \(\PageIndex{10}\) - \(\PageIndex{24}\), a matrix \(A\) and vector \(\vec{b}\) are given.

    1. Solve the equation \(A\vec{x}=\vec{0}\).
    2. Solve the equation \(A\vec{x}=\vec{b}\).

    In each of the above, be sure to write your answer in vector format. Also, when possible, give 2 particular solutions to each equation.

    Exercise \(\PageIndex{10}\)

    \(A=\left[\begin{array}{cc}{0}&{2}\\{-1}&{3}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-2}\\{-1}\end{array}\right]\)

    Answer
    1. \(\vec{x}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-2}\\{-1}\end{array}\right]\)
    Exercise \(\PageIndex{11}\)

    \(A=\left[\begin{array}{cc}{-4}&{-1}\\{-3}&{-2}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{1}\\{4}\end{array}\right]\)

    Answer
    1. \(\vec{x}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{2/5}\\{-13/5}\end{array}\right]\)
    Exercise \(\PageIndex{12}\)

    \(A=\left[\begin{array}{cc}{1}&{-2}\\{0}&{1}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{0}\\{-5}\end{array}\right]\)

    Answer
    1. \(\vec{x}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-10}\\{-5}\end{array}\right]\)
    Exercise \(\PageIndex{13}\)

    \(A=\left[\begin{array}{cc}{1}&{0}\\{5}&{-4}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-2}\\{-1}\end{array}\right]\)

    Answer
    1. \(\vec{x}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-2}\\{-9/4}\end{array}\right]\)
    Exercise \(\PageIndex{14}\)

    \(A=\left[\begin{array}{cc}{2}&{-3}\\{-4}&{6}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{1}\\{-1}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{2}\left[\begin{array}{c}{3/2}\\{1}\end{array}\right]\)
    2. No solution.
    Exercise \(\PageIndex{15}\)

    \(A=\left[\begin{array}{ccc}{-4}&{3}&{2}\\{-4}&{5}&{0}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-4}\\{-4}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{3}\left[\begin{array}{c}{5/4}\\{1}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]+x_{3}\left[\begin{array}{c}{5/4}\\{1}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{16}\)

    \(A=\left[\begin{array}{ccc}{1}&{5}&{-2}\\{1}&{4}&{5}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{0}\\{1}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{3}\left[\begin{array}{c}{-33}\\{7}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{5}\\{-1}\\{0}\end{array}\right]+x_{3}\left[\begin{array}{c}{-33}\\{7}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{17}\)

    \(A=\left[\begin{array}{ccc}{-1}&{-2}&{-2}\\{3}&{4}&{-2}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-4}\\{-4}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{3}\left[\begin{array}{c}{14}\\{-10}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-4}\\{2}\end{array}\right]+x_{3}\left[\begin{array}{c}{14}\\{-10}\\{0}\end{array}\right]\)
    Exercise \(\PageIndex{18}\)

    \(A=\left[\begin{array}{ccc}{2}&{2}&{2}\\{5}&{5}&{-3}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{3}\\{-3}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{2}\left[\begin{array}{c}{-1}\\{1}\\{0}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{3/16}\\{0}\\{21/16}\end{array}\right]+x_{2}\left[\begin{array}{c}{-1}\\{1}\\{0}\end{array}\right]\)
    Exercise \(\PageIndex{19}\)

    \(A=\left[\begin{array}{cccc}{1}&{5}&{-4}&{-1}\\{1}&{0}&{-2}&{1}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{0}\\{-2}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{3}\left[\begin{array}{c}{2}\\{2/5}\\{1}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{-1}\\{2/5}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-2}\\{2/5}\\{0}\\{0}\end{array}\right]+x_{3}\left[\begin{array}{c}{2}\\{2/5}\\{1}\\{0}\end{array}\right]+\left[\begin{array}{c}{-1}\\{2/5}\\{0}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{20}\)

    \(A=\left[\begin{array}{cccc}{-4}&{2}&{-5}&{4}\\{0}&{1}&{-1}&{5}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-3}\\{-2}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{3}\left[\begin{array}{c}{-3/4}\\{1}\\{1}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{-3/2}\\{-5}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-1/4}\\{-2}\\{0}\\{0}\end{array}\right]+x_{3}\left[\begin{array}{c}{-3/4}\\{1}\\{1}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{-3/2}\\{-5}\\{0}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{21}\)

    \(A=\left[\begin{array}{ccccc}{0}&{0}&{2}&{1}&{4}\\{-2}&{-1}&{-4}&{-1}&{5}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{3}\\{4}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{2}\left[\begin{array}{c}{-1/2}\\{1}\\{0}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{1/2}\\{0}\\{-1/2}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{13/2}\\{0}\\{-2}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{-5}\\{0}\\{3/2}\\{0}\\{0}\end{array}\right]+x_{2}\left[\begin{array}{c}{-1/2}\\{1}\\{0}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{1/2}\\{0}\\{-1/2}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{13/2}\\{0}\\{-2}\\{0}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{22}\)

    \(A=\left[\begin{array}{ccccc}{3}&{0}&{-2}&{-4}&{5}\\{2}&{3}&{2}&{0}&{2}\\{-5}&{0}&{4}&{0}&{5}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-1}\\{-5}\\{4}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{4}\left[\begin{array}{c}{8}\\{-12}\\{10}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{-15}\\{68/3}\\{-20}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{2}\\{-16/3}\\{7/2}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{8}\\{-12}\\{10}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{-15}\\{68/3}\\{-20}\\{0}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{23}\)

    \(A=\left[\begin{array}{ccccc}{-1}&{3}&{1}&{-3}&{4}\\{3}&{-3}&{-1}&{1}&{-4}\\{-2}&{3}&{-2}&{-3}&{1}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{1}\\{1}\\{-5}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{4}\left[\begin{array}{c}{1}\\{13/9}\\{-1/3}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{0}\\{-1}\\{-1}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{1}\\{1/9}\\{5/3}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{1}\\{13/9}\\{-1/3}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{0}\\{-1}\\{-1}\\{0}\\{1}\end{array}\right]\)
    Exercise \(\PageIndex{24}\)

    \(A=\left[\begin{array}{ccccc}{-4}&{-2}&{-1}&{4}&{0}\\{5}&{-4}&{3}&{-1}&{1}\\{4}&{-5}&{3}&{1}&{-4}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{3}\\{2}\\{1}\end{array}\right]\)

    Answer
    1. \(\vec{x}=x_{4}\left[\begin{array}{c}{3}\\{-1}\\{-6}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{-17}\\{12}\\{44}\\{0}\\{1}\end{array}\right]\)
    2. \(\vec{x}=\left[\begin{array}{c}{7}\\{-6}\\{-19}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{3}\\{-1}\\{-6}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{-17}\\{12}\\{44}\\{0}\\{1}\end{array}\right]\)

    In Exercises \(\PageIndex{25}\) – \(\PageIndex{28}\), a matrix \(A\) and vector \(\vec{b}\) are given. Solve the equation \(A\vec{x}=\vec{b}\), write the solution in vector format, and sketch the solution as the appropriate line on the Cartesian plane.

    Exercise \(\PageIndex{25}\)

    \(A=\left[\begin{array}{cc}{2}&{4}\\{-1}&{-2}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)

    Answer

    \(\vec{x}=x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right]=x_{2}\vec{v}\)

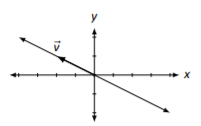
    clipboard_e46b1e81e74ff69bc1efa2b1870096469.png

    Figure \(\PageIndex{1}\)

    Exercise \(\PageIndex{26}\)

    \(A=\left[\begin{array}{cc}{2}&{4}\\{-1}&{-2}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{-6}\\{3}\end{array}\right]\)

    Answer

    \(\vec{x}=\left[\begin{array}{c}{-3}\\{0}\end{array}\right]+x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right]=\vec{x_{p}}+x_{2}\vec{v}\)

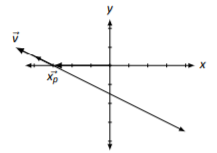
    clipboard_e7d4233acc2411f64fc8a317bbb81083d.png

    Figure \(\PageIndex{2}\)

    Exercise \(\PageIndex{27}\)

    \(A=\left[\begin{array}{cc}{2}&{-5}\\{-4}&{-10}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{1}\\{2}\end{array}\right]\)

    Answer

    \(\vec{x}=\left[\begin{array}{c}{0.5}\\{0}\end{array}\right]+x_{2}\left[\begin{array}{c}{2.5}\\{1}\end{array}\right]=\vec{x_{p}}+x_{2}\vec{v}\)

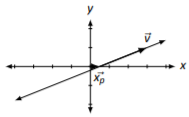
    clipboard_ea192547b7ad69a2b0fd1db5a3a424ecd.png

    Figure \(\PageIndex{3}\)

    Exercise \(\PageIndex{28}\)

    \(A=\left[\begin{array}{cc}{2}&{-5}\\{-4}&{-10}\end{array}\right],\:\vec{b}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]\)

    Answer

    \(\vec{x}=x_{2}\left[\begin{array}{c}{2.5}\\{1}\end{array}\right]=x_{2}\vec{v}\)

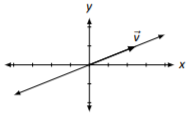
    clipboard_e2f219edc40fad5b66c9b65f8d39bc499.png

    Figure \(\PageIndex{4}\)

    2.4.1: Exercises 2.4 is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      License Version
      2.0
    2. Tags
      This page has no tags.