Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

16: Kernel, Range, Nullity, Rank

Last updated

Jul 27, 2023
Save as PDF
- 15.1: Review Problems
- 16.1: Summary

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Given a linear transformation $L \colon V \to W\, ,$ we want to know if it has an inverse, $\textit{i.e.}$ , is there a linear transformation $M \colon W \to V$ such that for any vector $v \in V$ , we have $MLv=v\, ,$ and for any vector $w \in W$ , we have $LMw=w\, .$ A linear transformation is just a special kind of function from one vector space to another. So before we discuss which linear transformations have inverses, let us first discuss inverses of arbitrary functions. When we later specialize to linear transformations, we'll also find some nice ways of creating subspaces.

Let $f \colon S \to T$ be a function from a set $S$ to a set $T$ . Recall that $S$ is called the $\textit{domain}$ of $f$ , $T$ is called the $\textit{codomain}$ or $\textit{target}$ of $f$ , and the set

${\rm ran}(f)={ \rm im}(f)=f(S)=\{ f(s) | s\in S \}\subset T\, ,$

is called the $\textit{range}$ or $\textit{image}$ of $f$ . The image of $f$ is the set of elements of $T$ to which the function $f$ maps, $\it{i.e.}$ , the things in $T$ which you can get to by starting in $S$ and applying $f$ . We can also talk about the pre-image of any subset $U \subset T$ :

$f^{-1}(U)=\{ s\in S | f(s)\in U \}\subset S.$

The pre-image of a set $U$ is the set of all elements of $S$ which map to $U$ .

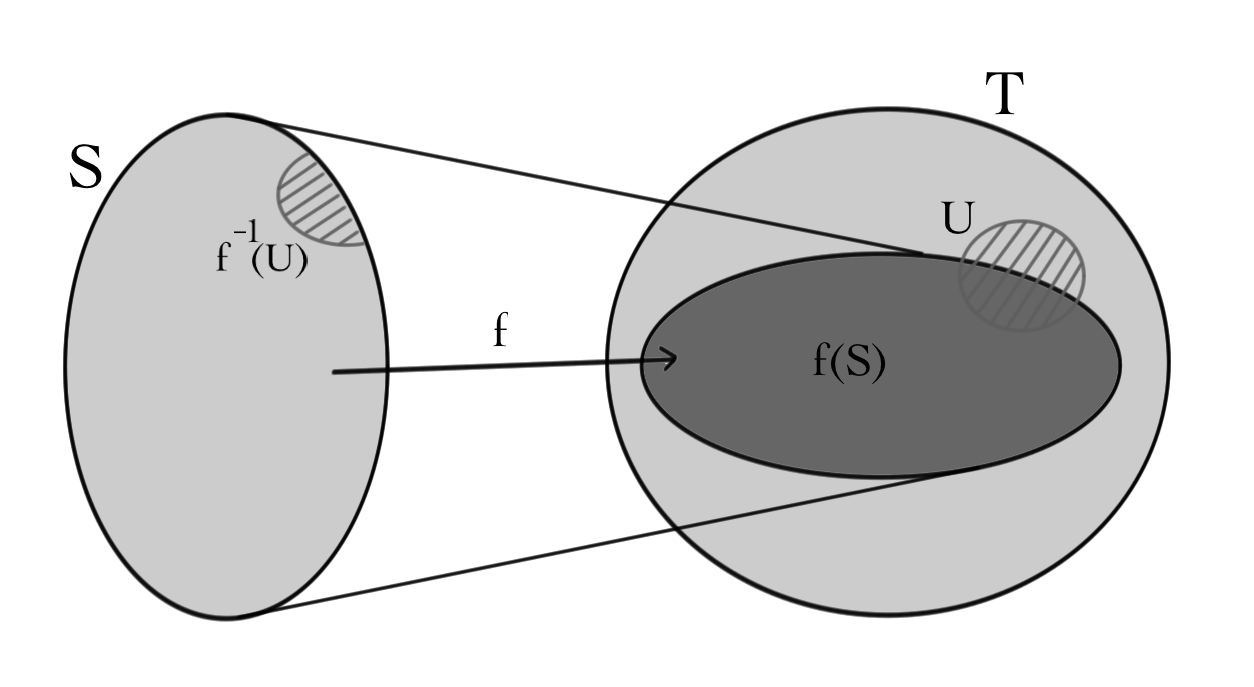
$functions.jpg$

For the function $f:S\to T$ , $S$ is the domain, $T$ is the target, $f(S)$ is the image/range and $f^{-1}(U)$ is the pre-image of $U\subset T$ .

The function $f$ is $\textit{one-to-one}$ if different elements in $S$ always map to different elements in $T$ . That is, $f$ is one-to-one if for any elements $x \neq y \in S,$ we have that $f(x) \neq f(y)$ :

$121.jpg$

One-to-one functions are also called $\textit{injective}$ functions. Notice that injectivity is a condition on the pre-images of $f$ .

The function $f$ is $\textit{onto}$ if every element of $T$ is mapped to by some element of $S$ . That is, $f$ is onto if for any $t \in T$ , there exists some $s \in S$ such that $f(s)=t$ . Onto functions are also called $\textit{surjective}$ functions. Notice that surjectivity is a condition on the image of $f$ :

$onto.jpg$

If $f$ is both injective and surjective, it is $\textit{bijective}$ :

$biject.jpg$

Theorem

A function $f \colon S \to T$ has an inverse function $g \colon T \to S$ if and only if it is bijective.

Proof

This is an "if and only if'' statement so the proof has two parts:

1. $\textit{(Existence of an inverse $\Rightarrow$ bijective.)}$

a) Suppose that $f$ has an inverse function $g$ . We need to show $f$ is bijective, which we break down into injective and surjective: The function $f$ is injective: Suppose that we have $s,s' \in S$ such that $f(x)=f(y)$ . We must have that $g(f(s))=s$ for any $s \in S$ , so in particular $g(f(s))=s$ and $g(f(s'))=s'$ . But since $f(s)=f(s'),$ we have $g(f(s))=g(f(s'))$ so $s=s'$ . Therefore, $f$ is injective.

b) The function $f$ is surjective: Let $t$ be any element of $T$ . We must have that $f(g(t))=t$ . Thus, $g(t)$ is an element of $S$ which maps to $t$ . So $f$ is surjective.

2. $\textit{(Bijectivity $\Rightarrow$ existence of an inverse.)}$

Suppose that $f$ is bijective. Hence $f$ is surjective, so every element $t \in T$ has at least one pre-image. Being bijective, $f$ is also injective, so every $t$ has no more than one pre-image. Therefore, to construct an inverse function $g$ , we simply define $g(t)$ to be the unique pre-image $f^{-1}(t)$ of $t$ .

Now let us specialize to functions $f$ that are linear maps between two vector spaces. Everything we said above for arbitrary functions is exactly the same for linear functions. However, the structure of vector spaces lets us say much more about one-to-one and onto functions whose domains are vector spaces than we can say about functions on general sets. For example, we know that a linear function always sends $0_{V}$ to $0_{W}$ , $\textit{i.e.}$ , $f(0_{V})=0_{W}.$ In review exercise 3, you will show that a linear transformation is one-to-one if and only if $0_{V}$ is the only vector that is sent to $0_{W}$ : In contrast to arbitrary functions between sets, by looking at just one (very special) vector, we can figure out whether $f$ is one-to-one!

Let $L \colon V \to W$ be a linear transformation. Suppose $L$ is \emph{not} injective. Then we can find $v_{1} \neq v_{2}$ such that $Lv_{1}=Lv_{2}$ . So $v_{1}-v_{2}\neq 0$ , but $L(v_{1}-v_{2})=0.$

Definition: linear transformation

Let $L \colon V\rightarrow W$ be a linear transformation. The set of all vectors $v$ such that $Lv=0_{W}$ is called the $\textit{kernel of $L$}$ :

$\ker L = \{v\in V | Lv=0_{W} \}\subset V.$

Theorem

A linear transformation $L$ is injective if and only if $$\ker L=\{ 0_{V} \}\, .\]

Proof
The proof of this theorem is review exercise 2.

Notice that if $L$ has matrix $M$ in some basis, then finding the kernel of $L$ is equivalent to solving the homogeneous system

$MX=0.$

Example $\PageIndex{1}$ :

Let $L(x,y)=(x+y,x+2y,y)$ . Is $L$ one-to-one?

To find out, we can solve the linear system:

\[ $\begin{pmatrix}1&1&0\\1&2&0\\0&1&0\end{pmatrix}$ \sim $\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}$ $$

Then all solutions of $MX=0$ are of the form $x=y=0$ . In other words, $\ker L=\{0\}$ , and so $L$ is injective.

Theorem

Let $L \colon V\stackrel{\rm linear}{-\!\!\!-\!\!\!-\!\!\!\rightarrow} W$ . Then $\ker L$ is a subspace of $V$ .

Notice that if $L(v)=0$ and $L(u)=0$ , then for any constants $c,d$ , $L(cu+dv)=0$ . Then by the subspace theorem, the kernel of $L$ is a subspace of $V$ .

Example $\PageIndex{2}$ :

Let $L \colon \Re^{3} \to \Re$ be the linear transformation defined by $L(x,y,z)=(x+y+z)$ . Then $\ker L$ consists of all vectors $(x,y,z) \in \Re^{3}$ such that $x+y+z=0$ . Therefore, the set
$V=\{(x,y,z) \in \Re^{3} \mid x+y+z=0\}$
is a subspace of $\Re^{3}$ .

When $L:V\to V$ , the above theorem has an interpretation in terms of the eigenspaces of $L$ : Suppose $L$ has a zero eigenvalue. Then the associated eigenspace consists of all vectors $v$ such that $Lv=0v=0$ ; in other words, the $0$ -eigenspace of $L$ is exactly the kernel of $L$ .

In the example where $L(x,y)=(x+y,x+2y,y)$ , the map $L$ is clearly not surjective, since $L$ maps $\Re^{2}$ to a plane through the origin in $\Re^{3}$ . But any plane through the origin is a subspace. In general notice that if $w=L(v)$ and $w'=L(v')$ , then for any constants $c,d$ , linearity of $L$ ensures that $cw+dw' = L(cv+dv')\, .$ Now the subspace theorem strikes again, and we have the following theorem:

Theorem

Let $L \colon V\rightarrow W$ . Then the image $L(V)$ is a subspace of $W$ .

Example $\PageIndex{3}$ :

Let $L(x,y)=(x+y,x+2y,y)$ . The image of $L$ is a plane through the origin and thus a subspace of $\mathbb{R}^{3}$ . Indeed the matrix of $L$ in the standard basis is
$\begin{pmatrix}1&1\\1&2\\0&1\end{pmatrix}\, .$
The columns of this matrix encode the possible outputs of the function $L$ because
$L(x,y)=\begin{pmatrix}1&1\\1&2\\0&1\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=x \begin{pmatrix}1\\1\\0\end{pmatrix}+y\begin{pmatrix}1\\2\\1\end{pmatrix}\, .$
Thus
$L({\mathbb R}^{2})=span \left\{\begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}1\\2\\1\end{pmatrix}\right\}$
Hence, when bases and a linear transformation is are given, people often refer to its image as the $\textit{column space}$ of the corresponding matrix.

To find a basis of the image of $L$ , we can start with a basis $S=\{v_{1}, \ldots, v_{n}\}$ for $V$ . Then
the most general input for $L$ is of the form $\alpha^{1} v_{1} + \cdots + \alpha^{n} v_{n}$ . In turn, its most general output looks like
$L\big(\alpha^{1} v_{1} + \cdots + \alpha^{n} v_{n}\big)=\alpha^{1} Lv_{1} + \cdots + \alpha^{n} Lv_{n}\in span \{Lv_{1},\ldots\,Lv_{n}\}\, .$
Thus
$L(V)=span L(S) = span \{Lv_{1}, \ldots, Lv_{n}\}\, .$
However, the set $\{Lv_{1}, \ldots, Lv_{n}\}$ may not be linearly independent; we must solve
$c^{1}Lv_{1}+ \cdots + c^{n}Lv_{n}=0\, ,$
to determine whether it is. By finding relations amongst the elements of $L(S)=\{Lv_{1},\ldots ,L v_{n}\}$ , we can discard vectors until a basis is arrived at. The size of this basis is the dimension of the image of $L$ , which is known as the $\textit{rank}$ of $L$ .

Definition

The $\textit{rank}$ of a linear transformation $L$ is the dimension of its image, written $rank L=\dim L(V) = \dim\, \textit{ran}\, L.$
The $\textit{nullity}$ of a linear transformation is the dimension of the kernel, written $nul L=\dim \ker L.$

Theorem: Dimension formula

Let $L \colon V\rightarrow W$ be a linear transformation, with $V$ a finite-dimensional vector space. Then:
$\begin{eqnarray*} \dim V &=& \dim \ker V + \dim L(V)\\ &=& nul L + rank L. \end{eqnarray*}$

Pick a basis for $V$ :
$\{ v_{1},\ldots,v_{p},u_{1},\ldots, u_{q} \},$
where $v_{1},\ldots,v_{p}$ is also a basis for $\ker L$ . This can always be done, for example, by finding a basis for the kernel of $L$ and then extending to a basis for $V$ . Then $p=nul L$ and $p+q=\dim V$ . Then we need to show that $q=rank L$ . To accomplish this, we show that $\{L(u_{1}),\ldots,L(u_{q})\}$ is a basis for $L(V)$ .

To see that $\{L(u_{1}),\ldots,L(u_{q})\}$ spans $L(V)$ , consider any vector $w$ in $L(V)$ . Then we can find constants $c^{i}, d^{j}$ such that:
$\begin{eqnarray*} w &=& L(c^{1}v_{1} + \cdots + c^{p}v_{p}+d^{1}u_{1} + \cdots + d^{q}u_{q})\\ &=& c^{1}L(v_{1}) + \cdots + c^{p}L(v_{p})+d^{1}L(u_{1})+\cdots+d^{q}L(u_{q})\\ &=& d^1L(u_1)+\cdots+d^qL(u_q) \text{ since $L(v_i)=0$,}\\ \Rightarrow L(V) &=& span \{L(u_{1}), \ldots, L(u_{q}) \}. \end{eqnarray*}$

Now we show that $\{L(u_{1}),\ldots,L(u_{q})\}$ is linearly independent. We argue by contradiction: Suppose there exist constants $d^{j}$ (not all zero) such that
$\begin{eqnarray*} 0 &=& d^{1}L(u_{1})+\cdots+d^{q}L(u_{q})\\ &=& L(d^{1}u_{1}+\cdots+d^{q}u_{q}).\\ \end{eqnarray*}$
But since the $u^{j}$ are linearly independent, then $d^{1}u_{1}+\cdots+d^{q}u_{q}\neq 0$ , and so $d^{1}u_{1}+\cdots+d^{q}u_{q}$ is in the kernel of $L$ . But then $d^{1}u_{1}+\cdots+d^{q}u_{q}$ must be in the span of $\{v_{1},\ldots, v_{p}\}$ , since this was a basis for the kernel. This contradicts the assumption that $\{ v_{1},\ldots,v_{p},u_{1},\ldots, u_{q} \}$ was a basis for $V$ , so we are done.

Contributor

David Cherney, Tom Denton, and Andrew Waldron (UC Davis)

Contributor

Support Center

How can we help?