17: Least Squares and Singular Values
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider the linear system L(x)=v, where L \colon U\stackrel{\textit{linear}}{-\!\!\!-\!\!\!\longrightarrow}W, and v\in W is given. As we have seen, this system may have no solutions, a unique solution, or a space of solutions. But if v is not in the range of L, in pictures:
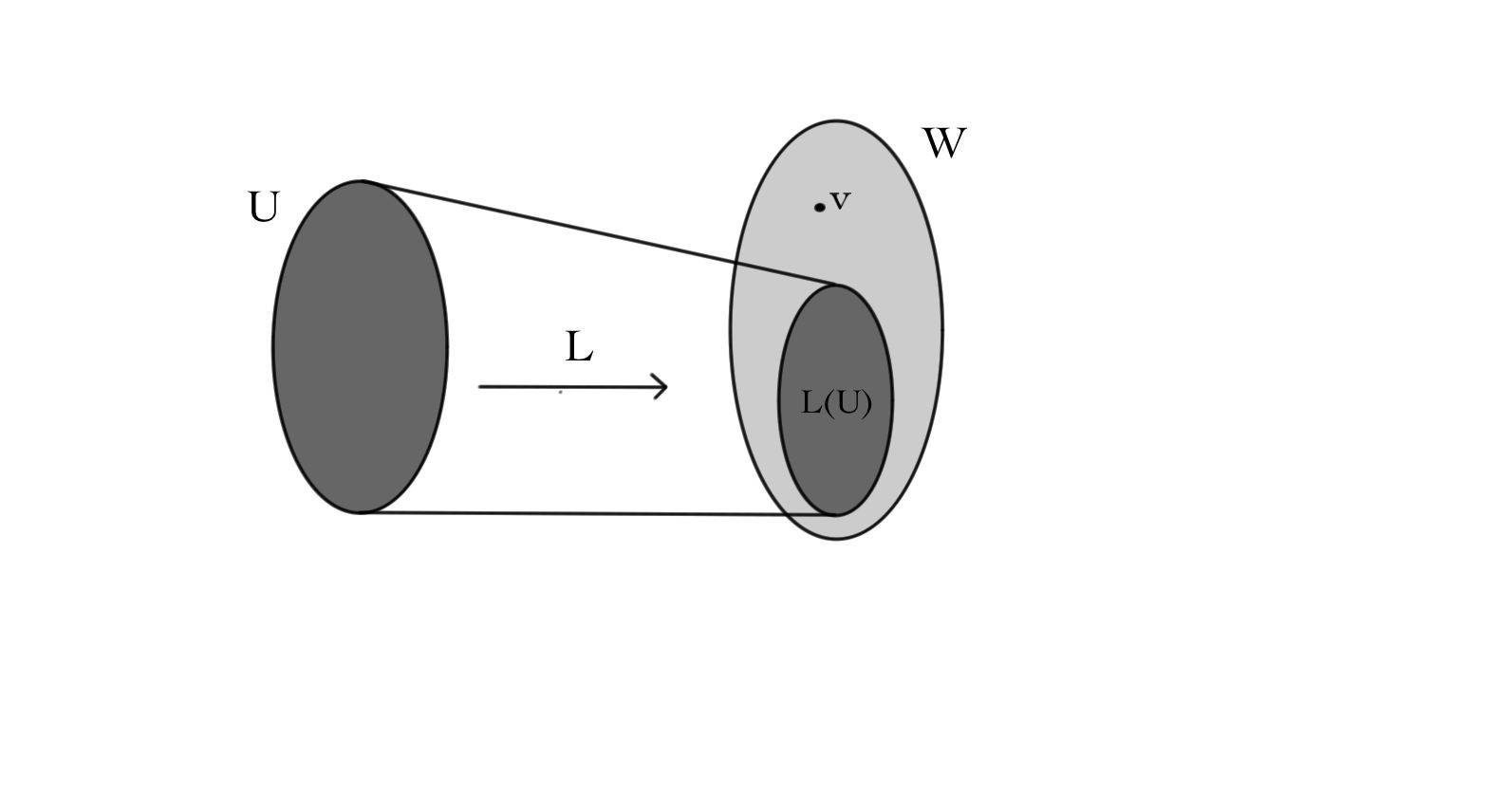
there will never be any solutions for L(x)=v. However, for many applications we do not need an exact solution of the system; instead, we try to find the best approximation possible.
"My work always tried to unite the Truth with the Beautiful, but when I had to choose one or the other, I usually chose the Beautiful.''--Hermann Weyl.
If the vector space W has a notion of lengths of vectors, we can try to find x that minimizes ||L(x)-v||:
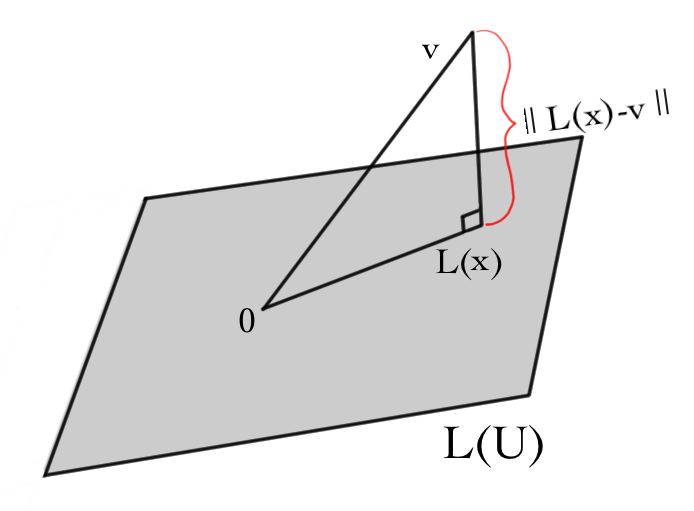
This method has many applications, such as when trying to fit a (perhaps linear) function to a "noisy'' set of observations. For example, suppose we measured the position of a bicycle on a racetrack once every five seconds. Our observations won't be exact, but so long as the observations are right on average, we can figure out a best-possible linear function of position of the bicycle in terms of time.
Suppose M is the matrix for L in some bases for U and W, and v and x are given by column vectors V and X in these bases. Then we need to approximate
MX-V\approx 0\, .
Note that if \dim U=n and \dim W=m then M can be represented by an m\times n matrix and x and v as vectors in \Re^{n} and \Re^{m}, respectively. Thus, we can write W=L(U)\oplus L(U)^{\perp}. Then we can uniquely write v=v^{\parallel} + v^{\perp}, with v^{\parallel} \in L(U) and v^{\perp} \in L(U)^{\perp}.
Thus we should solve L(u)=v^{\parallel}. In components, v^{\perp} is just V-MX, and is the part we will eventually wish to minimize.
In terms of M, recall that L(V) is spanned by the columns of M. (In the standard basis, the columns of M are Me_{1}, \ldots, Me_{n}.) Then v^{\perp} must be perpendicular to the columns of M. \textit{i.e.}, M^{T}(V-MX)=0, or
M^{T}MX = M^{T}V.
Solutions of M^{T}MX = M^{T}V for X are called \textit{least squares} solutions to MX=V. Notice that any solution X to MX=V is a least squares solution. However, the converse is often false. In fact, the equation MX=V may have no solutions at all, but still have least squares solutions to M^{T}MX = M^{T}V.
Observe that since M is an m\times n matrix, then M^{T} is an n\times m matrix. Then M^{T}M is an n\times n matrix, and is symmetric, since (M^{T}M)^{T}=M^{T}M. Then, for any vector X, we can evaluate X^{T}M^{T}MX to obtain a number. This is a very nice number, though! It is just the length |MX|^{2} = (MX)^{T}(MX)=X^{T}M^{T}MX.
Now suppose that \ker L=\{0\}, so that the only solution to MX=0 is X=0. (This need not mean that M is invertible because M is an n\times m matrix, so not necessarily square.) However the square matrix M^{T}M \textit{is} invertible. To see this, suppose there was a vector X such that M^{T} M X=0. Then it would follow that X^{T} M^{T} M X = |M X|^{2}=0. In other words the vector MX would have zero length, so could only be the zero vector. But we are assuming that \ker L=\{0\} so MX=0 implies X=0. Thus the kernel of M^{T}M is \{0\} so this matrix is invertible. So, in this case, the least squares solution (the X that solves M^{T}MX=MV) is unique, and is equal to
X = (M^{T}M)^{-1}M^{T}V.
In a nutshell, this is the least squares method:
- Compute M^{T}M and M^{T}V.
- Solve (M^{T}M)X=M^{T}V by Gaussian elimination.
Example \PageIndex{1}:
Captain Conundrum falls off of the leaning tower of Pisa and makes three (rather shaky) measurements of his velocity at three different times.
\begin{array}{r|r} t s & v m/s \\ \hline 1 & 11 \\ 2 & 19 \\ 3 & 31\end{array}
Having taken some calculus, he believes that his data are best approximated by a straight line
v = at+b.
Then he should find a and b to best fit the data.
\begin{eqnarray*}
11 &=& a\cdot 1 + b \\
19 &=& a\cdot 2 + b \\
31 &=& a\cdot 3 + b.
\end{eqnarray*}
As a system of linear equations, this becomes:
\begin{pmatrix} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ \end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix} \stackrel{?}{=} \begin{pmatrix}11\\19\\31\end{pmatrix}.
There is likely no actual straight line solution, so instead solve M^{T}MX=M^{T}V.
\begin{pmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ \end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ \end{pmatrix} \begin{pmatrix}11\\19\\31\end{pmatrix}.
This simplifies to the system:
\begin{pmatrix}14&6&142\\6&3&61\end{pmatrix} \sim \begin{pmatrix}1&0&10\\0&1&\frac{1}{3}\end{pmatrix}
Thus, the least-squares fit is the line
v = 10\ t + \frac{1}{3}\, .
Notice that this equation implies that Captain Conundrum accelerates towards Italian soil at 10 m/s^{2} (which is an excellent approximation to reality) and that he started at a downward velocity of \frac{1}{3} m/s (perhaps somebody gave him a shove...)!
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


