7.1: Relations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Recall from Section 5.4 that the Cartesian product of two sets
Let
For example, since California and Oregon have a land border, we can say that (California, Oregon)
- Use the roster method to specify the elements in each of the following sets:
(a)
(b)
(c) - Find two different examples of two ordered pairs
For all - Is the following conditional statement true or false? Explain.
For all
In Section 2.3, we introduced the concept of the truth set of an open sentence with one variable. This was defined to be the set of all elements in the universal set that can be substituted for the variable to make the open sentence a true proposition. Assume that
is an open sentence with two variables. An element of the truth set of this open sentence (also called a solution of the equation) is an ordered pair
When a set is a truth set of an open sentence that is an equation, we also call the set the solution set of the equation.
- List four different elements of the set
- The graph of the equation
- Describe each of the following sets as an interval of real numbers:
(a)
(b)
Introduction to Relations
In Section 6.1, we introduced the formal definition of a function from one set to another set. The notion of a function can be thought of as one way of relating the elements of one set with those of another set (or the same set). A function is a special type of relation in the sense that each element of the first set, the domain, is “related” to exactly one element of the second set, the codomain.
This idea of relating the elements of one set to those of another set using ordered pairs is not restricted to functions. For example, we may say that one integer,
we can say that 5 is related to 3, 5 is related to 2, and 5 is related to -1. Notice that, as with functions, each relation of the form
Let
A relation from the set
In Section 6.1, we defined the domain and range of a function. We make similar definitions for a relation.
If
We use the notation dom(
dom(
range(
A relation was studied in each of the Preview Activities for this section. For Preview Activity 2, the set
dom(
range(
So from the results in Preview Activity
- Let
(a) Explain why
(b) Find all values of
(c) What is the domain of the relation
(d) Since - From Preview Activity
(a) Explain why
(b) What is the domain of the relation
(c) Are the following statements true or false? Justify your conclusions.
i. For all
ii. For all
- Answer
-
Add texts here. Do not delete this text first.
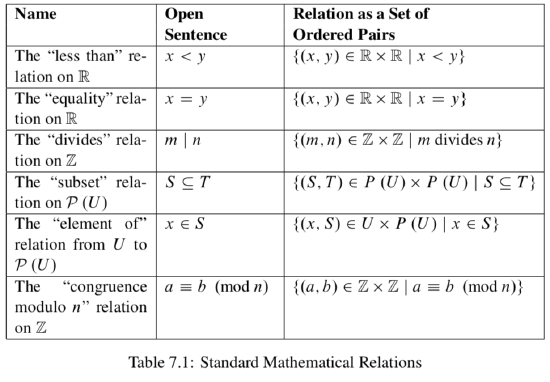
Some Standard Mathematical Relations
There are many different relations in mathematics. For example, two real numbers can be considered to be related if one number is less than the other number. We call this the "less than" relation on
\{R_{<} = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x < y\}\).
With many mathematical relations, we do not write the relation as a set of ordered pairs even though, technically, it is a set of ordered pairs. Table 7.1 describes some standard mathematical relations.
Notation for Relations
The mathematical relations in Table 7.1 all used a relation symbol between the two elements that form the ordered pair in
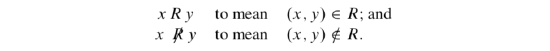
In some cases, we will even use a generic relation symbol for defining a new relation or speaking about relations in a general context. Perhaps the most commonly use symbol is "~", read “tilde” or “squiggle” or “is related to.” When we do this, we will write
Whenever we have spoken about one integer dividing another integer, we have worked with the “divides” relation on
In this case, we have a specific notation for “divides,” and we write
- What is the domain of the “divides” relation? What is the range of the “divides” relation?
- Are the following statements true or false? Explain.
(a) For every nonzero integer
(b) For all nonzero integers
(c) For all nonzero integers
- Answer
-
Add texts here. Do not delete this text first.
Functions as Relations
If we have a function
This means that
(1) For every
When
(2) For every
This means that a function
Let
- List five different ordered pairs that are in the set
- Use the roster method to specify the elements of each of the following the sets:
(a)
(b)
(c)
(d) - Since each real number
- Answer
-
Add texts here. Do not delete this text first.
Visual Representations of Relations
In Progress Check 7.4, we were able to draw a graph of a relation as a way to visualize the relation. In this case, the relation was a function from
When
then we can use the following graph as a way to visualize the points in the plane that are also in this relation.
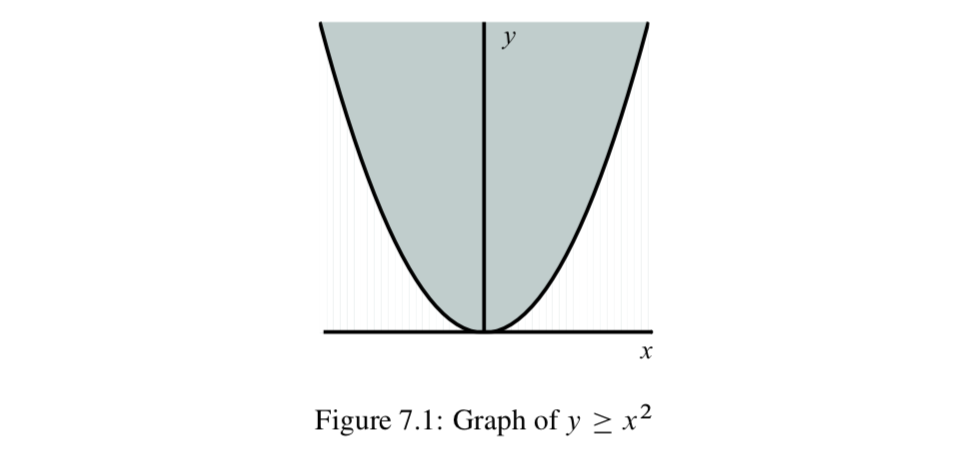
The points
When the domain or range of a relation is infinite, we cannot provide a visualization of the entire relation. However, if
is a relation on
In a directed graph, the points are called the vertices. So each element of
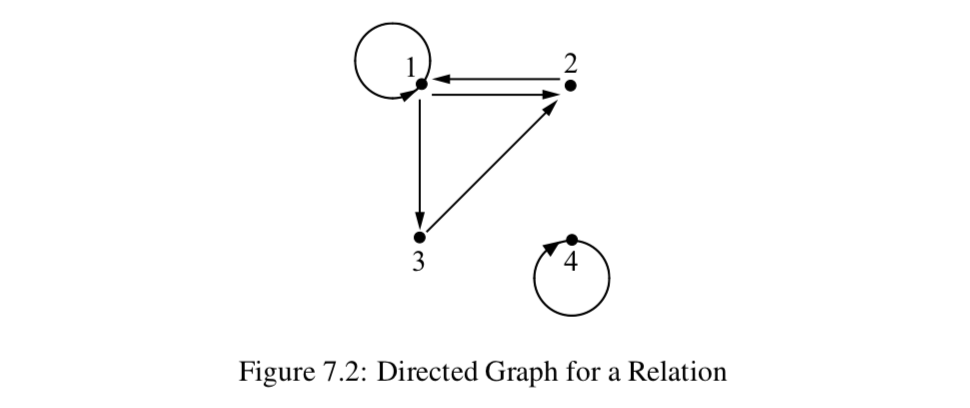
Let
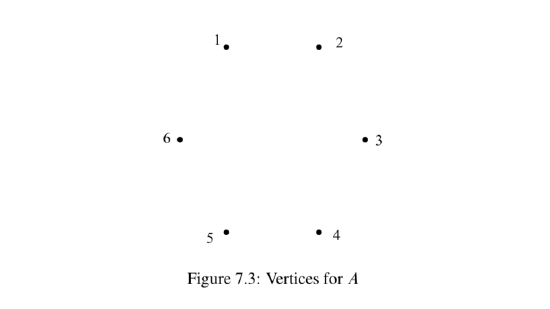
- Answer
-
Add texts here. Do not delete this text first.
- Let
(a) Use the roster method to list all the elements of
(b) Explain why
(c) What is the domain of - Let
(a) For each
(b) For every
(c) For every
(d) - Let
That is,
(a) Describe those elements of
(b) Describe those elements of
(c) Is the relation - Let
(a) Write the open sentence
(b) What is the domain of this subset relation,
(c) What is the range of this subset relation,
(d) Is - Let
(a) What is the domain of this “element of” relation,
(b) What is the range of this "element of" relation,
(c) Is - Let
(a) Determine the set of all values of
(b) Determine the domain and range of the relation
(c) Is the relation
(d) Since - Repeat Exercise( 6) using the relation on
What is the connection between this relation and the relation in Exercise (6)? - Determine the domain and range of each of the following relations on
(a)
(b)
(c)
(d) - Let
(a) Use set builder notation to describe the relation
(b) Determine the domain and range of the relation
(c) Use the roster method to specify these to fall integers
(d) If possible, find integers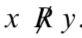 .
.
(e) If - Let
(a) What is the domain of the relation
(b) What is the range of the relation
(c) Is the relation
Note: Remember that a relation is a set. Consequently, we can talk about one relation being a subset of another relation. Another thing to remember is that the elements of a relation are ordered pairs.
Explorations and Activities - The Inverse of a Relation. In Section 6.5, we introduced the inverse of a function. If
Now that we know about relations, we see thatLet
That is,
For example, let
This means that we can write
Now, if we would like to focus on the first coordinate instead of the second coordinate in
We can say that the inverse of the “divides” relation on
Theorem 7.6, which follows, contains some elementary facts about inverse.Let
- The domain of
- The range of
- The inverse of
To prove the first part of Theorem 7.6, observe that the goal is to prove that two sets are equal,
dom(
One way to do this is to prove that each is a subset of the other. To prove that dom(
Now what does it mean to say that
Complete the proof of the first part of Theorem 7.6. Then, complete the proofs of the other two parts of Theorem 7.6.
- Proof
-
Add proof here and it will automatically be hidden
- The domain of
- Answer
-
Add texts here. Do not delete this text first.


