6.1: Introduction to Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Preview Activity 1 (Functions from Previous Courses)
One of the most important concepts in modern mathematics is that of a function. In previous mathematics courses, we have often thought of a function as some sort of input-output rule that assigns exactly one output to each input. So in this context, a function can be thought of as a procedure for associating with each element of some set, called the domain of the function, exactly one element of another set, called the codomain of the function. This procedure can be considered an input-output-rule. The function takes the input, which is an element of the domain, and produces an output, which is an element of the codomain. In calculus and precalculus, the inputs and outputs were almost always real numbers. So the notationf f(x)=x2sinx means the following:
- f is the name of the function.
- f(x) is a real number. It is the output of the function when the input is the real number x. For example,
f(π2)=(π2)2sin(π2)=π24⋅1=π24.
For this function, it is understood that the domain of the function is the set R of all real numbers. In this situation, we think of the domain as the set of all possible inputs. That is, the domain is the set of all possible real numbers x for which a real number output can be determined.
This is closely related to the equation f=x2sinx. With this equation, we frequently think of x as the input and y as the output. In fact, we sometimes write y=f(x). The key to remember is that a function must have exactly one output for each input. When we write an equation such as
y=12x3−1,
we can use this equation to define y as a function of x. This is because when we substitute a real number for x (the input), the equation produces exactly one real number for y (the output). We can give this function a name, such as g, and write
y=g(x)=12x3−1.
However, as written, an equation such as
y2=x+3
cannot be used to define y as a function of x since there are real numbers that can be substituted for x that will produce more than one possible value of y. For example, if x=1, then y2=4, and y could be -2 or 2.
Which of the following equations can be used to define a function with x∈R as the input and y∈R as the output?
- y=x2−2
- y2=x+3
- y=12x3−1
- y=12xsinx
- x2+y2=4
- y=2x−1
- y=dfracxx−1
The domain and codomain of the functions in Preview Activity 6.1.1 is the set R of all real numbers, or some subset of R. In most of these cases, the way in which the function associates elements of the domain with elements of the codomain is by a rule determined by some mathematical expression. For example, when we say that f is the function such that
f(x)=xx−1,
then the algebraic rule that determines the output of the function f when the input is x is xx−1. In this case, we would say that the domain of f is the set of all real numbers not equal to 1 since division by zero is not defined.
However, the concept of a function is much more general than this. The domain and codomain of a function can be any set, and the way in which a function associates elements of the domain with elements of the codomain can have many different forms. The input-output rule for a function can be a formula, a graph, a table, a random process, or a verbal description. We will explore two different examples in this preview activity.
- Let b be the function that assigns to each person his or her birthday (month and day). The domain of the function b is the set of all people and the codomain of b is the set of all days in a leap year (i.e., January 1 through December 31, including February 29).
(a) Explain why b really is a function. We will call this the birthday function.
(b) In 1995, Andrew Wiles became famous for publishing a proof of Fermat’s Last Theorem. (See A. D. Aczel, Fermat’s Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem, Dell Publishing, New York, 1996.) Andrew Wiles’s birthday is April 11, 1953. Translate this fact into functional notation using the “birthday function” b. That is, fill in the spaces for the following question marks: b(?)=?.
(c) Is the following statement true or false? Explain.
For each day D of the year, there exists a person x such that b(x)=D.
(d) Is the following statement true or false? Explain.
For any people x and y, if x and y are different people, then b(x)≠b(y). - Let s be the function that associates with each natural number the sum of its distinct natural number divisors. This is called the sum of the divisors function. For example, the natural number divisors of 6 are 1, 2, 3, and 6, and so
s(6)=1+2+3+6=12.
(a) Calculate s(k) for each natural number k from 1 through 15.
(b) Does there exist a natural number n such that s(n)=5? Justify your conclusion.
(c) Is it possible to find two different natural numbers m and n such that s(m)=s(n)? Explain.
(d) Use your responses in (b) and (c) to determine whether the following statements true or false.
i. For each m∈N, there exists a natural number n such that s(n)=m.
ii. For all m,n∈N, if m≠n, then s(m)≠s(n).
The Definition of a Function
The concept of a function is much more general than the idea of a function used in calculus or precalculus. In particular, the domain and codomain do not have to be subsets of R. In addition, the way in which a function associates elements of the domain with elements of the codomain can have many different forms. This input-output rule can be a formula, a graph, a table, a random process, a computer algorithm, or a verbal description. Two such examples were introduced in Preview Activity 6.1.2.
For the birthday function, the domain would be the set of all people and the codomain would be the set of all days in a leap year. For the sum of the divisors function, the domain is the set N of natural numbers, and the codomain could also be N. In both of these cases, the input-output rule was a verbal description of how to assign an element of the codomain to an element of the domain.
We formally define the concept of a function as follows:
A function from a set A to a set B is a rule that associates with each element x of the set A exactly one element of the set B. A function from A to B is also called a mapping from A to B.
Function Notation. When we work with a function, we usually give it a name. The name is often a single letter, such as f or g. If f is a function from the set A to be the set B, we will write f:A→B. This is simply shorthand notation for the fact that f is a function from the set A to the set B. In this case, we also say that f maps A to B.
Let f:A→B. (This is read, “Let f be a function from A to B.”) The set A is called the domain of the function f, and we write A=dom(f). The set B is called the codomain of the function f, and we write B=codom(f).
If a∈A, then the element of B that is associated with a is denoted by f(a) and is called the image of a under f. If f(a)=b, with b∈B, then a is called a preimage of b under f.
Some Function Terminology with an Example. When we have a function f:A→B, we often write y=f(x). In this case, we consider x to be an unspecified object that can be chosen from the set A, and we would say that x is the independent variable of the function f and y is the dependent variable of the function f.
For a specific example, consider the function g:R→R, where g(x) is defined by the formula
g(x)=x2−2.
Note that this is indeed a function since given any input x in the domain, R, there is exactly one output g(x) in the codomain, R. For example,
g(−2)=(−2)2−2=2,g(5)=52−2=23,g(√2)=(√2)2−2=0,g(−√2)=(−√2)2−2=0.
So we say that the image of -2 under g is 2, the image of 5 under g is 23, and so on.
Notice in this case that the number 0 in the codomain has two preimages, −√2 and √2. This does not violate the mathematical definition of a function since the definition only states that each input must produce one and only one output. That is, each element of the domain has exactly one image in the codomain. Nowhere does the definition stipulate that two different inputs must produce different outputs.
Finding the preimages of an element in the codomain can sometimes be difficult. In general, if y is in the codomain, to find its preimages, we need to ask, “For which values of x in the domain will we have y=g(x)?” For example, for the function g, to find the preimages of 5, we need to find all x for which g(x)=5. In this case, since g(x)=x2−2, we can do this by solving the equation
x2−2=5.
The solutions of this equation are −√7 and √7. So for the function g, the preimages of 5 are −√7 and √7. We often use set notation for this and say that the set of preimages of 5 for the function g is {−√7, √7}.
Also notice that for this function, not every element in the codomain has a preimage. For example, there is no input x such that g(x)=−3. This is true since for all real numbers x, x2≥0 and hence x2−2≥−2. This means that for all x in R, g(x)≥−2.
Finally, note that we introduced the function g with the sentence, “Consider the function g:R→R, where g(x) is defined by the formula g(x)=x2−2.” This is one correct way to do this, but we will frequently shorten this to, “Let g:R→R be defined by g(x)=x2−2”, or “Let g:R→R, where g(x)=x2−2.”
Let f:R→R be defined by f(x)=x2−5x for all x∈R. and let g:Z→Z be defined by g(m)=m2−5m for all m∈Z.
- Determine f(−3) and f(√8).
- Determine g(2) and g(−2).
- Determine the set of all preimage of 6 for the function f.
- Determine the set of all preimage of 6 for the function g.
- Determine the set of all preimage of 2 for the function f.
- Determine the set of all preimage of 2 for the function g.
- Answer
-
Add texts here. Do not delete this text first.
The Codomain and Range of a Function
Besides the domain and codomain, there is another important set associated with a function. The need for this was illustrated in the example of the function g on page 285. For this function, it was noticed that there are elements in the codomain that have no preimage or, equivalently, there are elements in the codomain that are not the image of any element in the domain. The set we are talking about is the subset of the codomain consisting of all images of the elements of the domain of the function, and it is called the range of the function.
Let f:A→B. The set {f(x) | x∈A} is called the range of the function f and is denoted by range (f). The range of f is sometimes called the image of the function f (or the image of A under f).
The range of f:A→B could equivalently be defined as follows:
range(f)={y∈B | y=f(x) for some x∈A}.
Notice that this means that range(f) ⊆ codom(f) but does not necessarily mean that range(f) = codom(f). Whether we have this set equality or not depends on the function f. More about this will be explored in Section 6.3.
- Let b be the function that assigns to each person his or her birthday (month and day).
(a) What is the domain of this function?
(b) What is a codomain for this function?
(c) In Preview Activity 6.1.2, we determined that the following statement is true: For each day D of the year, there exists a person x such that b(x)=D. What does this tell us about the range of the function b? Explain. - Let s be the function that associates with each natural number the sum of its distinct natural number factors.
(a) What is the domain of this function?
(b) What is a codomain for this function?
(c) In Preview Activity 6.1.2, we determined that the following statement is false:
For each m∈N, there exists a natural number n such that s(n)=m.
Give an example of a natural number m that shows this statement is false, and explain what this tells us about the range of the function s.
- Answer
-
Add texts here. Do not delete this text first.
The Graph of a Real Function
We will finish this section with methods to visually communicate information about two specific types of functions. The first is the familiar method of graphing functions that was a major part of some previous mathematics courses. For example, consider the function g:R→R defined by g(x)=x2−2x−1.
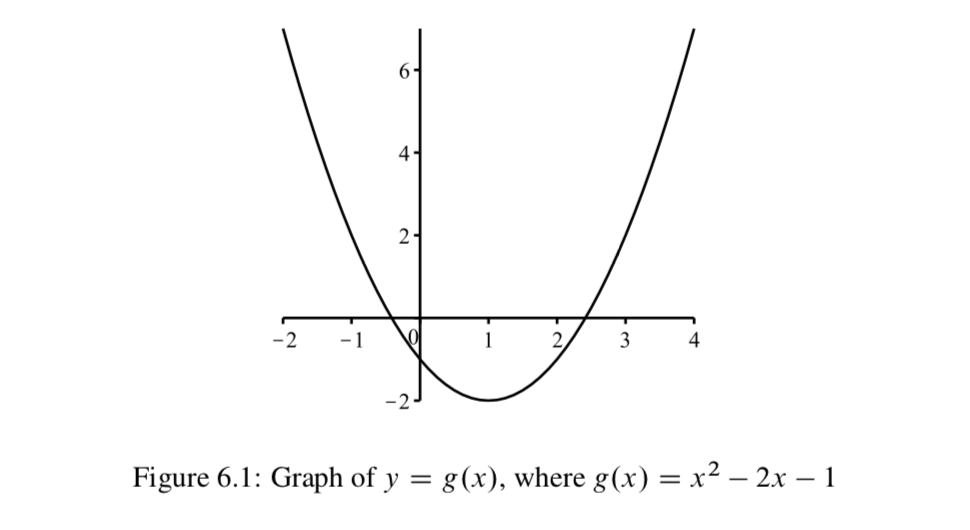
Every point on this graph corresponds to an ordered pair (x, y) of real numbers, where y=g(x)=x2−2x−1. Because we use the Cartesian plane when drawing this type of graph, we can only use this type of graph when both the domain and the codomain of the function are subsets of the real numbers R. Such a function is sometimes called a real function. The graph of a real function is a visual way to communicate information about the function. For example, the range of g is the set of all y-values that correspond to points on the graph. In this case, the graph of g is a parabola and has a vertex at the point (1, -2). (Note: The x-coordinate of the vertex can be found by using calculus and solving the equation f′(x)=0.) Since the graph of the function g is a parabola, we know that pattern shown on the left end and the right end of the graph continues and we can conclude that the range of g is the set of all y∈R such that y≥−2. That is,
range(g)={y∈R | y≥−2}.
The graph in Figure 6.2 shows the graph of (slightly more than) two complete periods for a function f:R→R, where f(x)=Asin(Bx) for some positive real number constants A and B.
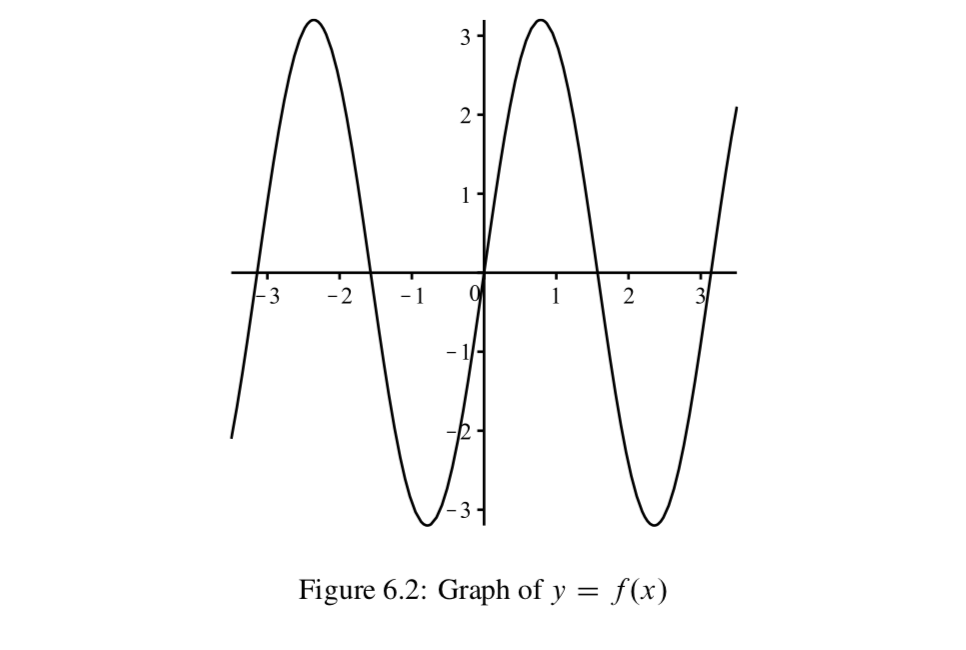
- We can use the graph to estimate the output for various inputs. This is done by estimating the y-coordinate for the point on the graph with a specified x-coordinate. On the graph, draw vertical lines at x=−1 and x=2 and estimate the values of f(−1) and f(2).
- Similarly, we can estimate inputs of the function that produce a specified output. This is done by estimating the x-coordinates of the points on the graph that have a specified y-coordinate. Draw a horizontal line at y=2 and estimate at least two values of x such that f(x)=2.
- Use the graph Figure 6.2 to estimate the range of the function f.
- Answer
-
Add texts here. Do not delete this text first.
Arrow Diagrams
Sometimes the domain and codomain of a function are small, finite sets. When this is the case, we can define a function simply by specifying the outputs for each input in the domain. For example, if we let A={1,2,3} and let B={a,b}, we can define a function F:A→B by specifying that
F(1)=a,F(2)=a, and F(3)=b.
This is a function since each element of the domain is mapped to exactly one element in B. A convenient way to illustrate or visualize this type of function is with a so-called arrow diagram as shown in Figure 6.3. An arrow diagram can
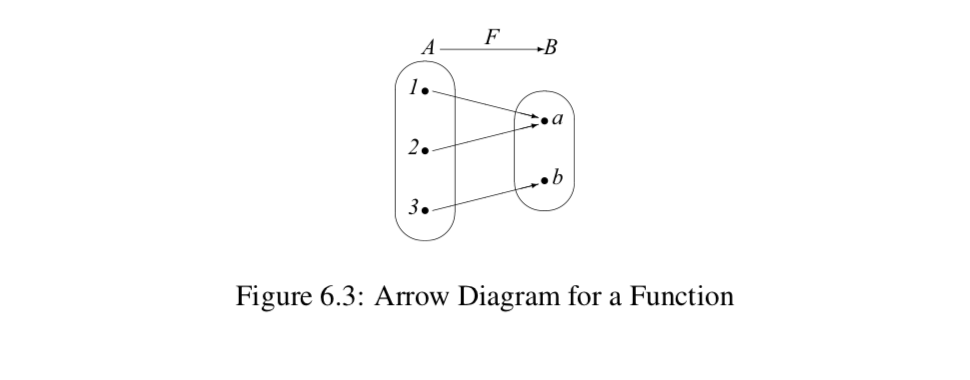
be used when the domain and codomain of the function are finite (and small). We represent the elements of each set with points and then use arrows to show how the elements of the domain are associated with elements of the codomain. For example, the arrow from the point 2 in A to the point a in B represents the fact that F(2)=a. In this case, we can use the arrow diagram in Figure 6.3 to conclude that range(F)={a,b}.
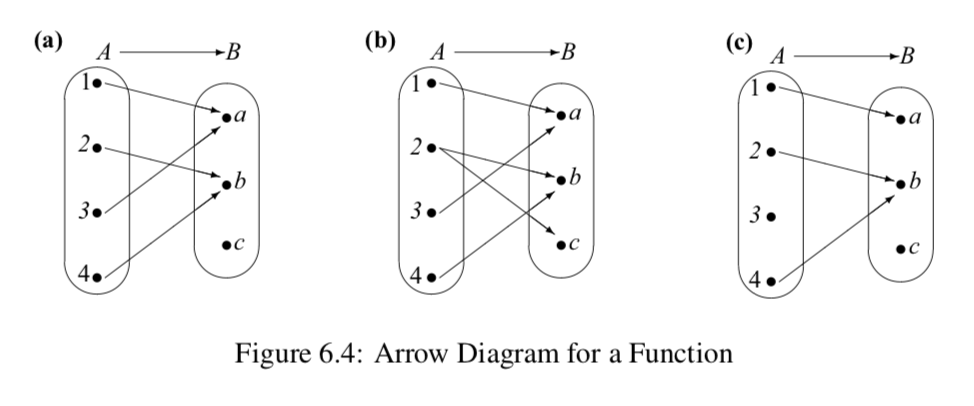
Let A={1,2,3,4} and let B={a,b,c}.
- Which of the arrow diagrams in Figure 6.4 can be used to represent a function from A to B? Explain.
- For those arrow diagrams that can be used to represent a function from A to B, determine the range of the function.
- Answer
-
Add texts here. Do not delete this text first.
- Let f:R→R be defined by f(x)=x2−2x.
(a) Evaluate f(−3), f(−1), f(1), and f(3).
(b) Determine the set of all of the preimages of 0 and the set of all of the preimages of 4.
(c) Sketch a graph of the function f.
(d) Determine the range of the function f. - Let R∗={x∈R | x≥0}, and let s:R→R∗ be defined by s(x)=x2.
(a) Evaluate s(−3), s(−1), s(1), and s(3).
(b) Determine the set of all of the preimages of 0 and the set of all of the preimages of 2.
(c) Sketch a graph of the function s.
(d) Determine the range of the function s. - Let f:Z→Z be defined by f(m)=3−m.
(a) Evaluate f(−7), f(−3), f(3), and f(7).
(b) Determine the set of all of the preimages of 5 and the set of all of the preimages of 4.
(c) Determine the range of the function f.
(d) This function can be considered a real function since Z⊆R. Sketch a graph of this function. Note: The graph will be an infinite set of points that lie on a line. However, it will not be a line since its domain is not R but is Z. - Let f:Z→Z be defined by f(m)=2m+1.
(a) Evaluate f(−7), f(−3), f(3), and f(7).
(b) Determine the set of all of the preimages of 5 and the set of all of the preimages of 4.
(c) Determine the range of the function f.
(d) Sketch a graph of the function f. See the comments in Exercise (3d). - Recall that a real function is a function whose domain and codomain are subsets of the real numbers R. (See page 288.) Most of the functions used in calculus are real functions. Quite often, a real function is given by a formula or a graph with no specific reference to the domain or the codomain. In these cases, the usual convention is to assume that the domain of the real function f is the set of all real numbers x for which f(x) is a real number, and that the codomain is R. For example, if we define the (real) function f by
f(x)=xx−2,
we would be assuming that the domain is the set of all real numbers that are not equal to 2 and that the codomain in R.
Determine the domain and range of each of the following real functions. It might help to use a graphing calculator to plot a graph of the function.
(a) The function k defined by k(x)=√x−3
(b) The function F defined by F(x)=ln(2x−1)
(c) The function f defined by f(x)=3sin(2x)
(d) The function g defined by g(x)=4x2−4
(e) The function G defined by G(x)=4cos(πx)+8 - The number of divisors function. Let d be the function that associates with each natural number the number of its natural number divisors. That is d:N→N where d(n) is the number of natural number divisors of n. For example, d(6)=4 since 1, 2, 3, and 6 are the natural number divisors of 6.
(a) Calculate d(k) for each natural number k from 1 through 12.
(b) Does there exist a natural number n such that d(n)=1? What is the set of preimages of the natural number 1.
(c) Does there exist a natural number n such that d(n)=2? If so, determine the set of all preimages of the natural number 2.
(d) Is the following statement true or false? Justify your conclusion.
For all m,n∈N, if m≠n, then d(m)≠d(n).
(e) Calculate d(2k) for k=0 and for each natural number k from 1 through 6.
(f) Based on your work in Exercise (6e), make a conjecture for a formula for d(2n) where n is a nonnegative integer. Then explain why your conjecture is correct.
(g) Is the following statement is true or false?
For each n∈N, there exists a natural number m such that d(m)=n. - In Exercise (6), we introduced the number of divisors function d. For this function, d:N→N, where d(n) is the number of natural number divisors of n.
A function that is related to this function is the so-called set of divisors function. This can be defined as a function S that associates with each natural number the set of its distinct natural number factors. For example, S(6)={1,2,3,6} and S(10)={1,2,5,10}.
(a) Discuss the function S by carefully stating its domain, codomain, and its rule for determining outputs.
(b) Determine S(n) for at least five different values of n.
(c) Determine S(n) for at least three different prime number values of n.
(d) Does there exist a natural number n such that card(S(n)=1)? Explain. [Recall that card(S(n)) is the number of elements in the set S(n).]
(e) Does there exist a natural number n such that card(S(n)=2)? Explain.
(f) Write the output for the function d in terms of the output for the function S. That is, write d(n) in terms of S(n).
(g) Is the following statement true or false? Justify your conclusion.
For all natural numbers m and n, if m≠n, then S(m)≠S(n).
(h) Is the following statement true or false? Justify your conclusion.
For all sets T that are subsets of N, there exists a natural number n such that S(n)=T.
Explorations and Activities - Creating Functions with Finite Domains. Let A={a,b,c,d}, B={a,b,c}. and C={s,t,u,v}. In each of the following exercises, draw an arrow diagram to represent your function when it is appropriate.
(a) Create a function f:A→C whose range is the set C or explain why it is not possible to construct such a function.
(b) Create a function f:A→C whose range is the set {u,v} or explain why it is not possible to construct such a function.
(c) Create a function f:B→C whose range is the set C or explain why it is not possible to construct such a function.
(d) Create a function f:A→C whose range is the set {u} or explain why it is not possible to construct such a function.
(e) If possible, create a function f:A→C that satisfies the following condition:
For all x,y∈A, if x≠y, then f(x)≠f(y).
If it is not possible to create such a function, explain why.
(f) If possible, create a function f:A→{s,t,u} that satisfies the following condition:
For all x,y∈A, if x≠y, then f(x)≠f(y).
If it is not possible to create such a function, explain why.
- Answer
-
Add texts here. Do not delete this text first.


