6.5: Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
The concept of a function is one of the most useful abstractions in mathematics. In fact, it is an abstraction that can be further abstracted! For instance, an operator is an entity which takes functions as inputs and produces functions as outputs, thus an operator is to functions as functions themselves are to numbers. There are many operators that you have certainly encountered already – just not by that name. One of the most famous operators is “differentiation,” when you take the derivative of some function, the answer you obtain is another function. If two different people are given the same differentiation problem and they come up with different answers, we know that at least one of them has made a mistake! Similarly, if two calculations of the value of a function are made for the same input, they must match.
The property we are discussing used to be captured by saying that a function needs to be “well-defined.” The old school definition of a function was:
A function f is a well-defined rule, that, given any input value x produces a unique output1 value f(x).
A more modern definition of a function is the following.
A function is a binary relation which does not contain distinct pairs having the same initial element.
When we think of a function as a special type of binary relation, the pairs that are “in” the function have the form (x,f(x)), that is, they consist of an input and the corresponding output.
We have gotten relatively used to relations “on” a set, but recall that the more general situation is that a binary relation is a subset of A×B. In this setting, if the relation is actually a function f, we say that f is a function from A to B. Now, quite often there are input values that simply don’t work for a given function (for instance the well-known “you can’t take the square root of a negative” rule). Also, it is often the case that certain outputs just can’t happen. So, when dealing with a function as a relation contained in A×B there are actually four sets that are of interest – the sets A and B (of course) but also some sets that we’ll denote by A′ and B′. The set A′ consists of those elements of A that actually appear as the first coordinate of a pair in the relation f. The set B′ consists of those elements of B that actually appear as the second coordinate of a pair in the relation f. A generic example of how these four sets might look is given in Figure 6.5.1.
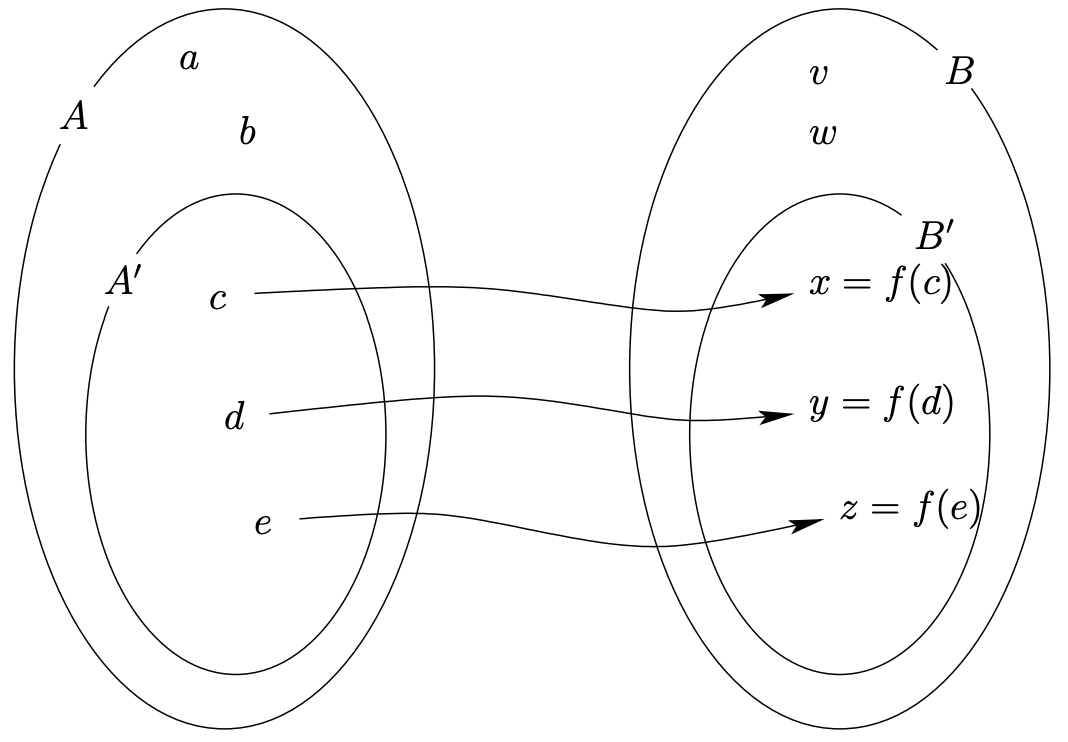
Sadly, only three of the sets we have just discussed are known to the mathematical world. The set we have denoted A′ is called the domain of the function f. The set we have denoted B′ is known as the range of the function f. The set we have denoted B is called the codomain of the function f. The set we have been calling A does not have a name. In fact, the formal definition of the term “function” has been rigged so that there is no difference between the sets A and A′. This seems a shame, if you think of range and domain as being primary, doesn’t it seem odd that we have a way to refer to a superset of the range (i.e. the codomain) but no way of referring to a superset of the domain?
Nevertheless, this is just the way it is . . . There is only one set on the input side – the domain of our function.
The domain of any relation is expressed by writing Dom(R). Which is defined as follows.
If R is a relation from A to B then Dom(R) is a subset of A defined by
Dom(R)={a∈A∃b∈B,(a,b)∈R}
We should point out that the notation just given for the domain of a relation R, Dom(R) has analogs for the other sets that are involved with a relation. We write Cod(R) to refer the the codomain of the relation, and Rng(R) to refer to the range.
Since we are now thinking of functions as special classes of relations, it follows that a function is just a set of ordered pairs. This means that the identity of a function is tied up, not just with a formula that gives the output for a given input, but also with what values can be used for those inputs. Thus the function f(x)=2x defined on R is a completely different animal from the function f(x)=2x defined on N. If you really want to specify a function precisely you must give its domain as well as a formula for it. Usually, one does this by writing a formula, then a semicolon, then the domain. (E.g. f(x)=x2;x≥0.)
Okay, so, finally, we are prepared to give the real definition of a function.
If A and B are sets, then f is a function from A to B (which is expressed symbolically by f:A⟶B), if and only if f is a subset of A×B, Dom(f)=A and ((a,b)∈f∧(a,c)∈f⟹b=c.
Recapping, a function must have its domain equal to the set A where its inputs come from. This is sometimes expressed by saying that a function is defined on its domain. A function’s range and codomain may be different however. In the event that the range and codomain are the same (Cod(R)=Rng(R)) we have a rather special situation and the function is graced by the appellation “surjection.” The term “onto” is also commonly used to describe a surjective function.
There is an expression in mathematics, “Every function is onto its range.” that really doesn’t say very much. Why not?
If one has elements x and y, of the domain and codomain, (respectively) and y=f(x)2 then one may say that “y is the image of x” or that “x is a preimage of y.” Take careful note of the articles used in these phrases – we say “y is the image of x” but “x is a preimage of y.” This is because y is uniquely determined by x, but not vice versa. For example, since the squares of 2 and −2 are both 4, if we consider the function f(x)=x2, the image of (say) 2 is 4, but a preimage for 4 could be either 2 or −2.
It would be pleasant if there were a nice way to refer to the preimage of some element, y, of the range. One notation that you have probably seen before is “f−1(y).” There is a major difficulty with writing down such a thing. By writing “f−1” you are making a rather vast presumption – that there actually is a function that serves as an inverse for f. Usually, there is not.
One can define an inverse for any relation, the inverse is formed by simply exchanging the elements in the ordered pairs that make up R.
The inverse relation of a relation R is denoted R−1 and
R−1={(y,x)(x,y)∈R}.
In terms of graphs, the inverse and the original relation are related by being reflections in the line y=x. It is possible for one, both, or neither of these to be functions. The canonical example to keep in mind is probably f(x)=x2 and its inverse.
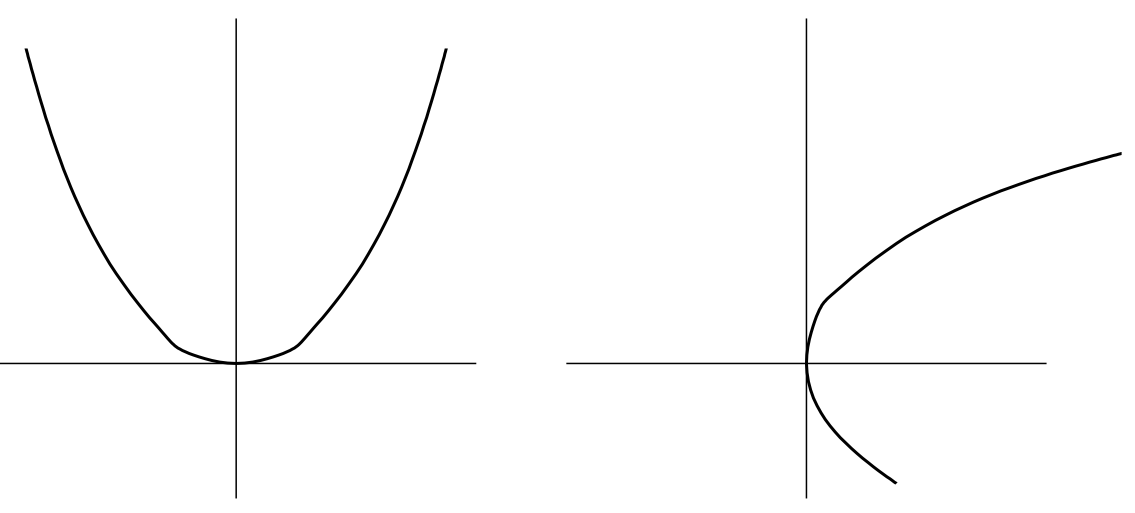
The graph that we obtain by reflecting y=f(x)=x2 in the line y=x doesn’t pass the vertical line test and so it is the graph of (merely) a relation – not of a function. The function g(x)=√x that we all know and love is not truly the inverse of f(x). In fact, this function is defined to make a specific (and natural) choice – it returns the positive square root of a number. But this leads to a subtle problem; if we start with a negative number (say −3) and square it we get a positive number (9) and if we then come along and take the square root we get another positive number (3). This is problematic since we didn’t end up where we started which is what ought to happen if we apply a function followed by its inverse.
We’ll try to handle the general situation in a bit, but for the moment let’s consider the nice case: when the inverse of a function is also a function. When exactly does this happen? Well, we have just seen that the inverse of a function doesn’t necessarily pass the vertical line test, and it turns out that that is the predominant issue. So, under what circumstances does the inverse pass the vertical line test? When the original function passes the so-called horizontal line test (every horizontal line intersects the graph at most once). Thinking again about f(x)=x2, there are some horizontal lines that miss the graph entirely, but all horizontal lines of the form y=c where c is positive will intersect the graph twice. There are many functions that do pass the horizontal line test, for instance, consider f(x)=x3. Such functions are known as injections, this is the same thing as saying a function is “one-toone.” Injective functions can be inverted – the domain of the inverse function of f will only be the range, Rng(f), which as we have seen may fall short of the being the entire codomain, since Rng(f)⊆Cod(f).
Let’s first define injections in a way that is divorced from thinking about their graphs.
A function f(x) is an injection iff for all pairs of inputs x1 and x2, if f(x1)=f(x2) then x1=x2.
This is another of those defining properties that is designed so that when it is true it is vacuously true. An injective function never takes two distinct inputs to the same output. Perhaps the cleanest way to think about injective functions is in terms of preimages – when a function is injective, preimages are unique. Actually, this is a good time to mention something about surjective functions and preimages – if a function is surjective, every element of the codomain has a preimage. So, if a function has both of these properties it means that every element of the codomain has one (and only one) preimage.
A function that is both injective and surjective (one-to-one and onto) is known as a bijection. Bijections are tremendously important in mathematics since they provide a way of perfectly matching up the elements of two sets. You will probably spend a good bit of time in the future devising maps between sets and then proving that they are bijections, so we will start practicing that skill now. . .
Ordinarily, we will show that a function is a bijection by proving separately that it is both a surjection and an injection.
To show that a function is surjective we need to show that it is possible to find a preimage for every element of the codomain. If we happen to know what the inverse function is, then it is easy to find a preimage for an arbitrary element. In terms of the taxonomy for proofs that was introduced in Chapter 3, we are talking about a constructive proof of an existential statement. A function f is surjective iff ∀y∈Cod(f),∃x∈Dom(f), y=f(x), so to prove surjectivity is to find the x that “works” for an arbitrary y. If this is done by literally naming x, we have proved the statement constructively.
To show that a function is an injection, we traditionally prove that the property used in the definition of an injective function is true. Namely, we suppose that x1 and x2 are distinct elements of Dom(f) and that f(x1)=f(x2) and then we show that actually x1=x2. This is in the spirit of a proof by contradiction – if there were actually distinct elements that get mapped to the same value then f would not be injective, but by deducing that x1=x2 we are contradicting that presumption and so, are showing that f is indeed an injection.
Let’s start by looking at a very simple example, f(x)=2x−1; x∈N. Clearly this function is not a surjection if we are thinking that Cod(f)=N since the outputs are always odd. Let O={1,3,5,7,...} be the set of odd naturals.
The function f:N⟹O defined by f(x)=2x−1 is a bijection from N to O.
- Proof
-
First we will show that f is surjective. Consider an arbitrary element y of the set O. Since y∈O it follows that y is both positive and odd. Thus there is an integer k, such that y=2k+1, but also y>0. From this it follows that 2k+1>0 and so k>−12. Since k is also an integer, this last inequality implies that k∈Znoneg. (Recall that Znoneg={0,1,2,3,...}.) We can easily verify that a preimage for y is k+1, since f(k+1)=2(k+1)−1=2k+2−1=2k+1=y.
Next we show that f is injective. Suppose that there are two input values, x1 and x2 such that f(x1)=f(x2). Then 2x1−1=2x2−1 and simple algebra leads to x1=x2.
Q.E.D.
For a slightly more complicated example consider the function from N to Z defined by
f(x)={x2 if x is even −(x−1)2 if x is odd
This function does quite a handy little job, it matches up the natural numbers and the integers in pairs. Every even natural gets matched with a positive integer and every odd natural (except 1) gets matched with a negative integer (1 gets paired with 0). This function is really doing something remarkable – common sense would seem to indicate that the integers must be a larger set than the naturals (after all N is completely contained inside of Z), but the function f defined above serves to show that these two sets are exactly the same size!
The function f defined above is bijective.
- Proof
-
First we will show that f is surjective.
It suffices to find a preimage for an arbitrary element of Z. Suppose that y is a particular but arbitrarily chosen integer. There are two cases to consider: y≤0 and y>0.
If y>0 then x=2y is a preimage for y. This follows easily since x=2y is obviously even and so x’s image will be defined by the first case in the definition of f. Thus f(x)=f(2y)=(2y)2=y.
If y≤0 then x=1−2y is a preimage for y. Clearly, 1−2y is odd whenever y is an integer, thus this value for x will fall into the second case in the definition of f. So, f(x)=f(1−2y)=−((1−2y)−1)2=−(−2y)2=y.
Since the cases y>0 and y≤0 are exhaustive (that is, every y in Z falls into one or the other of these cases), and we have found a preimage for y in both cases, it follows that f is surjective.
Next, we will show that f is injective.
Suppose that x1 and x2 are elements of N and that f(x1)=f(x2). Consider the following three cases: x1 and x2 are both even, both odd, or have opposite parity.
If x1 and x2 are both even, then by the definition of f we have f(x1)=x12 and f(x2)=x22 and since these functional values are equal, we have x12=x22. Doubling both sides of this leads to x1=x2.
If x1 and x2 are both odd, then by the definition of f we have f(x1)=−(x1−1)2 and f(x2)=−(x2−1)2 and since these functional values are equal, we have −(x1−1)2=−(x2−1)2. A bit more algebra (doubling, negating and adding one to both sides) leads to x1=x2.
If x1 and x2 have opposite parity, we will assume w.l.o.g. that x1 is even and x2 is odd. The equality f(x1)=f(x2) becomes x12=−(x2−1)2. Note that x1≥2 so f(x1)=x12≥1. Also, note that x2≥1 so
x2−1≥0((x2−1)2≥0−(x2−1)2≤0f(x2)≤0
therefore we have a contradiction since it is impossible for the two values f(x1) and f(x2) to be equal while f(x1)≥1 and f(x2)≤0.
Since the last case under consideration leads to a contradiction, it follows that x1 and x2 never have opposite parities, and so the first two cases are exhaustive – in both of those cases, we reached the desired conclusion that x1=x2 so it follows that f is injective.
Q.E.D.
We’ll conclude this section by mentioning that the ideas of “image” and “preimage” can be extended to sets. If S is a subset of Dom(f) then the image of S under f is denoted f(S) and
f(S)={y|∃x∈Dom(f),x∈S∧y=f(x)}.
Similarly, if T is a subset of Rng(f) we can define something akin to the preimage. The inverse image of the set T under the function f is denoted f−1(T) and
f−1(T)={x|∃y∈Cod(f),y∈T∧y=f(x)}.
Essentially, we have extended the function f so that it goes between the power sets of its codomain and range! This new notion gives us some elegant ways of restating what it means to be surjective and injective. A function f is surjective iff f(Dom(f))=Cod(f). A function f is injective iff the inverse images of singletons are always singletons. That is,
∀y∈Rng(f),∃x∈Dom(f),f−1(y)=x.
Exercises:
For each of the following functions, give its domain, range and a possible codomain.
- f(x)=sin(x)
- g(x)=ex
- h(x)=x2
- m(x)=x2+1x2−1
- n(x)=⌊x⌋
- p(x)=⟨cos(x),sin(x)⟩
Find a bijection from the set of odd squares, {1,9,25,49,...}, to the non-negative integers, Znoneg={0,1,2,3,...}. Prove that the function you just determined is both injective and surjective. Find the inverse function of the bijection above.
The natural logarithm function ln(x) is defined by a definite integral with the variable x in the upper limit.
ln(x)=∫xt=11tdt.
From this definition we can deduce that ln(x) is strictly increasing on its entire domain, (0,∞). Why is this true?
We can use the above definition with x=2 to find the value of ln(2)≈.693. We will also take as given the following rule (which is valid for all logarithmic functions).
ln(ab)=bln(a)
Use the above information to show that there is neither an upper bound nor a lower bound for the values of the natural logarithm. These facts together with the information that ln is strictly increasing show that Rng(ln)=R.
Georg Cantor developed a systematic way of listing the rational numbers. By “listing” a set one is actually developing a bijection from N to that set. The method known as “Cantor’s Snake” creates a bijection from the naturals to the non-negative rationals. First, we create an infinite table whose rows are indexed by positive integers and whose columns are indexed by non-negative integers – the entries in this table are rational numbers of the form “column index” / “row index.” We then follow a snake-like path that zig-zags across this table – whenever we encounter a rational number that we haven’t seen before (in lower terms) we write it down. This is indicated in the diagram below by circling the entries.
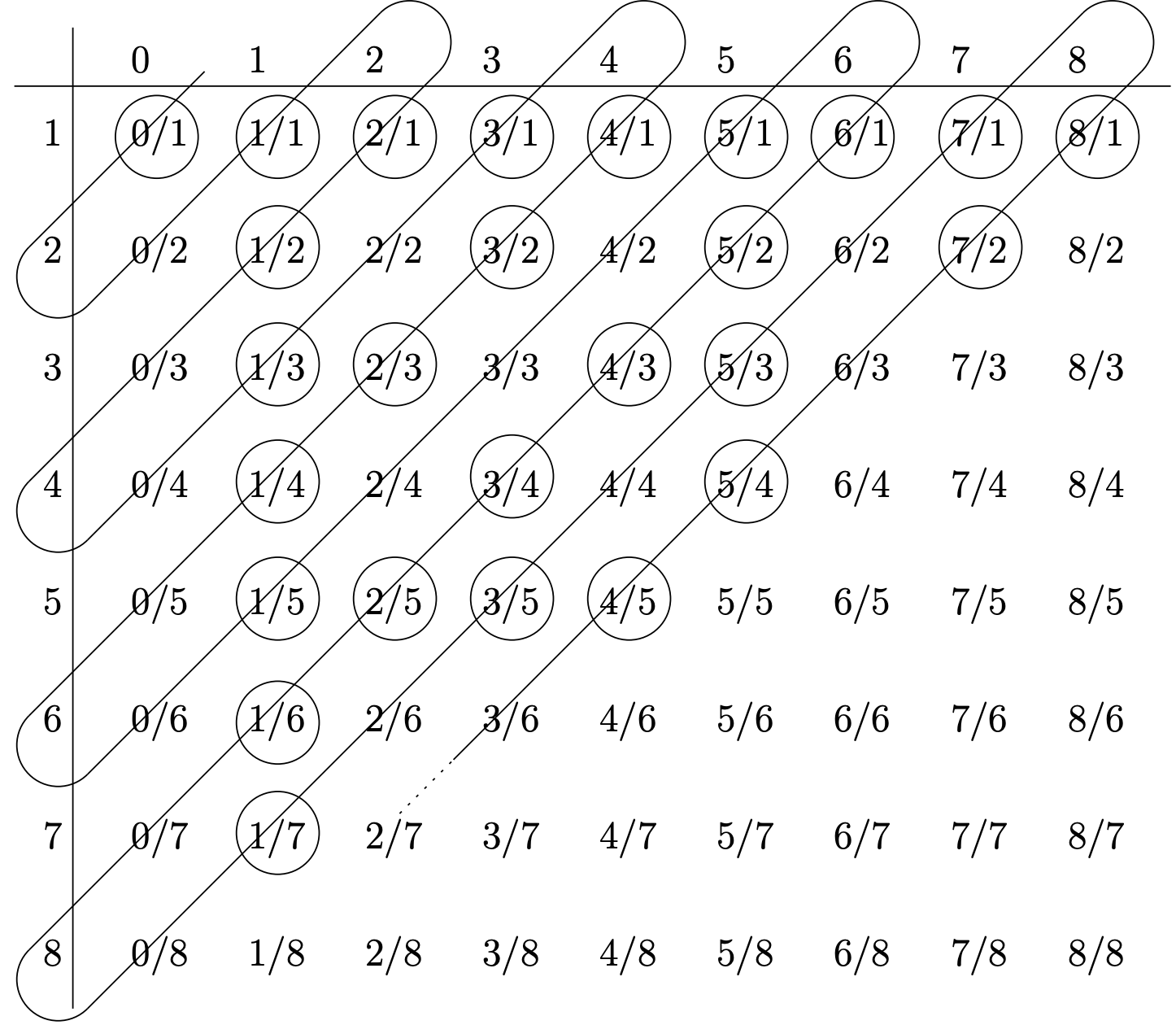
Effectively this gives us a function f which produces the rational number that would be found in a given position in this list. For example f(1)=01, f(2)=11 and f(5)=13.
What is f(26)? What is f(30)? What is f−1(34)? What is f−1(67)?



