9.2: Countable Sets

Preview Activity : Introduction to Infinite Sets

In Section 9.1, we defined a finite set to be the empty set or a set such that for some natural number . We also defined an infinite set to be a set that is not finite, but the question now is, “How do we know if a set is infinite?” One way to determine if a set is an infinite set is to use Corollary 9.8, which states that a finite set is not equivalent to any of its subsets. We can write this as a conditional statement as follows:

If is a finite set, then is not equivalent to any of its proper subsets. or more formally as

For each set , if is a finite set, then for each proper subset of , .

1. Write the contrapositive of the preceding conditional statement. Then explain how this statement can be used to determine if a set is infinite.
2. Let DC be the set of all odd natural numbers. In Preview Activity from Section 9.1, we proved that .

   (a) Use this to explain carefully why is an infinite set.
   (b) Is a finite set or an infinite set? Explain carefully how you know.

3. Let be a positive real number. Let (0, 1) and be the open intervals from 0 to 1 and 0 to , respectively. In Part (3) of Progress Check 9.2 (on page 454), we proved that .

   (a) Use a value for where to explain why (0, 1) is an infinite set.
   (b) Use a value for where to explain why is an infinite set.

Preview Activity : A Function from to

In this preview activity, we will define and explore a function . We will start by defining for the first few natural numbers .

Notice that if we list the outputs of in the order , , , ..., we create the following list of integers: 0, 1, -1, 2, -2, 3, -3, ... . We can also illustrate the outputs of this function with the following diagram:

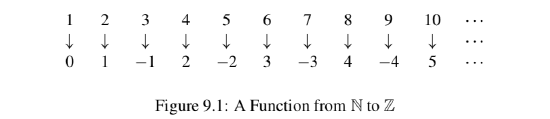
1. If the pattern suggested by the function values we have defined continues, what are and ? What is for from 13 to 16?
2. If the pattern of outputs continues, does the function appear to be an injection? Does appear to be a surjection? (Formal proofs are not required.)
   
   We will now attempt to determine a formula for , where . We will actually determine two formulas: one for when is even and one for when is odd.
3. Look at the pattern of the values of when is even. What appears to be a formula for when is even?
4. Look at the pattern of the values of when n is odd. What appears to be a formula for when is odd?
5. Use the work in Part (3) and Part (4) to complete the following: Define , where
   
6. Use the formula in Part (5) to (a) Calculate through . Are these results consistent with the pattern exhibited at the beginning of this preview activity?
   (b) Calculate and .
   (c) Determine the value of so that .

In this section, we will describe several infinite sets and define the cardinal number for so-called countable sets. Most of our examples will be subsets of some of our standard numbers systems such as , , and .

Infinite Sets

In Preview Activity , we saw how to use Corollary 9.8 to prove that a set is infinite. This corollary implies that if A is a finite set, then A is not equivalent to any of its proper subsets. By writing the contrapositive of this conditional statement, we can restate Corollary 9.8 in the following form:

Corollary 9.8

If a set is equivalent to one of its proper subsets, then is infinite.

In Preview Activity , we used Corollary 9.8 to prove that

• The set of natural numbers, , is an infinite set.
• The open interval (0, 1) is an infinite set.

Although Corollary 9.8 provides one way to prove that a set is infinite, it is sometimes more convenient to use a proof by contradiction to prove that a set is infinite. The idea is to use results from Section 9.1 about finite sets to help obtain a contra- diction. This is illustrated in the next theorem.

Theorem 9.10.

Let and be sets.

1. If is infinite and , then is infinite.
2. If is infinite and , then is infinite.

Proof

We will prove part (1). The proof of part (2) is exercise (3) on page 473.

To prove part (1), we use a proof by contradiction and assume that A is an infinite set, , and is not infinite. That is, is a finite set. Since and is finite, Theorem 9.3 on page 455 implies that is a finite set. This is a contradiction to the assumption that is infinite. We have therefore proved that if is infinite and , then is infinite.

Progress Check 9.11 (Examples of Infinite Sets)

1. In Preview Activity , we used Corollary 9.8 to prove that is an infinite set. Now use this and Theorem 9.10 to explain why our standard number systems (, , and ) are infinite sets. Also, explain why the set of all positive rational numbers, , and the set of all positive real numbers, , are infinite sets.
2. Let be the set of all odd natural numbers. In Part (2) of Preview Activity , we proved that . Use Theorem 9.10 to explain why is an infinite set.
3. Prove that the set of all even natural numbers is an infinite set.

Answer

Add texts here. Do not delete this text first.

Countably Infinite Sets

In Section 9.1, we used the set as the standard set with cardinality in the sense that a set is finite if and only if it is equivalent to . In a similar manner, we will use some infinite sets as standard sets for certain infinite cardinal numbers. The first set we will use is .

We will formally define what it means to say the elements of a set can be “counted” using the natural numbers. The elements of a finite set can be “counted” by defining a bijection (one-to-one correspondence) between the set and for some natural number . We will be able to “count” the elements of an infinite set if we can define a one-to-one correspondence between the set and .

Definition

The cardinality of is denoted by . The symbol is the first letter of the Hebrew alphabet, aleph. The subscript 0 is often read as “naught” (or sometimes as “zero” or “null”). So we write

and say that the cardinality of is “aleph naught.”

Definition

A set is countably infinite provided that . In this case, we write

A set that is countably infinite is sometimes called a denumerable set. A set is countable provided that it is finite or countably infinite. An infinite set that is not countably infinite is called an uncountable set.

progress check 9.12. (examples of countably infinite sets)

1. In Preview Activity from Section 9.1, we proved that , where is the set of all odd natural numbers. Explain why .
2. Use a result from Progress Check 9.11 to explain why .
3. At this point, if we wish to prove a set is countably infinite, we must find a bijection between the set and some set that is known to be countably infinite.

   Let be the set of all natural numbers that are perfect squares. Define a function

   
   that can be used to prove that and, hence, that .

Answer

Add texts here. Do not delete this text first.

The fact that the set of integers is a countably infinite set is important enough to be called a theorem. The function we will use to establish that was explored in Preview Activity .

Theorem 9.13

The set of integers is countably infinite, and so

Proof

To prove that , we will use the following funciton: , where

From our work in Preview Activity , it appears that if n is an even natural number, then , and if is an odd natural number, then . So it seems reasonable to use cases to prove that is a surjection and that is an injection. To prove that is a surjection, we let .

• If , then , and
  
• If , then and is an odd natural number. Hence,
  

These two cases prove that if , then there exists an such that . Hence, is a surjection.

To prove that is an injection, we let and assume that . First note that if one of and is odd and the other is even, then one of and is positive and the other is less than or equal to 0. So if , then both and must be even or both and must be odd.

• If both and are even, then
  
  and hence that .
• If both and are odd, then
  
  From this, we conclude that and hence that . This proves that if , then and hence that is an injection.

Since is both a surjection and an injection, we see that is a bijection and, therefore, . Hence, is countably infinite and .

The result in Theorem 9.13 can seem a bit surprising. It exhibits one of the distinctions between finite and infinite sets. If we add elements to a finite set, we will increase its size in the sense that the new set will have a greater cardinality than the old set. However, with infinite sets, we can add elements and the new set may still have the same cardinality as the original set. For example, there is a one-to-one correspondence between the elements of the sets and . We say that these sets have the same cardinality.

Following is a summary of some of the main examples dealing with the cardinality of sets that we have explored.

• The sets , where , are examples of sets that are countable and finite.
• The sets , , the set of all odd natural numbers, and the set of all even natural numbers are examples of sets that are countable and countably infinite.
• We have not yet proved that any set is uncountable.

The Set of Positive Rational Numbers

If we expect to find an uncountable set in our usual number systems, the rational numbers might be the place to start looking. One of the main differences between the set of rational numbers and the integers is that given any integer m, there is a next integer, namely . This is not true for the set of rational numbers. We know that is closed under division (by nonzero rational numbers) and we will see that this property implies that given any two rational numbers, we can also find a rational number between them. In fact, between any two rational numbers, we can find infinitely many rational numbers. It is this property that may lead us to believe that there are “more” rational numbers than there are integers.

The basic idea will be to “go half way” between two rational numbers. For example, if we use and , we can use

as a rational number between and . We can then repeat this process to find a rational number between and .

So we will now let and be any two rational numbers with and let . We then see that

Since , we see that and so the previous equations show that and . We can then conclude that .

We can now repeat this process by using and proving that , In fact, for each natural number, we can define

and obtain the result that and this proves that the set is a countably infinite set where each element is a rational number between and . (A formal proof can be completed using mathematical induction. See Exercise ().

This result is true no matter how close together and are. For example, we can now conclude that there are infinitely many rational numbers between 0 and This might suggest that the set of rational numbers is uncountable. Surprisingly, this is not the case. We start with a proof that the set of positive rational numbers is countable.

Theorem 9.14

The set of positive rational numbers is countably infinite.

Proof

We can write all the positive rational numbers in a two-dimensional array as shown in Figure 9.2. The top row in Figure 9.2 represents the numerator of the rational number, and the left column represents the denominator. We follow the arrows in Figure 9.2 to define . The idea is to start in the upper left corner of the table and move to successive diagonals as follows:

• We start with all fractions in which the sum of the numerator and denominator is 2 (only ). So .
  
• We next use those fractions in which the sum of the numerator and denominator is 3. So and .
• We next use those fractions in which the sum of the numerator and denominator is 4. So , . We skipped since . In this way, we will ensure that the function f is a one-to-one function.

We now continue with successive diagonals omitting fractions that are not in lowest terms. This process guarantees that the function will be an injection and a surjection. Therefore, and .

Note: For another proof of Theorem 9.14, see exercise (14) on page 475.

Since is countable, it seems reasonable to expect that is countable. We will explore this soon. On the other hand, at this point, it may also seem reasonable to ask,

"Are there any uncountable sets?”

The answer to this question is yes, but we will wait until the next section to prove that certain sets are uncountable. We still have a few more issues to deal with concerning countable sets.

Countably Infinite Sets

Theorem 9.15.

If is a countably infinite set, then is a countably infinite set.

Proof

Let be a countably infinite set. Then there exists a bijection . Since is either in or not in , we can consider two cases.

If , then and is countably infinite.

If , define by

The proof that the function is a bijection is Exercise (4). Since is a bijection, we have proved that and hence, is a countably infinite set.

Theorem 9.16.

If is a countably infinite set and is a finite set, then is a countably infinite set.

Proof

Exercise (5) on page 474.

Theorem 9.16 says that if we add a finite number of elements to a countably infinite set, the resulting set is still countably infinite. In other words, the cardinality of the new set is the same as the cardinality of the original set. Finite sets behave very differently in the sense that if we add elements to a finite set, we will change the cardinality. What may even be more surprising is the result in Theorem 9.17 that states that the union of two countably infinite (disjoint) sets is countably infinite. The proof of this result is similar to the proof that the integers are countably infinite (Theorem 9.13). In fact, if and , then we can use the following diagram to help define a bijection from to .

Theorem 9.17

If and are disjoint countably infinite sets, then is a countably infinite set.

Proof

Let and be countably infinite sets and let and be bijections. Define by

It is left as Exercise (6) on page 474 to prove that the function is a bijection.

Since we can write the set of rational numbers Q as the union of the set of nonnegative rational numbers and the set of rational numbers, we can use the results in Theorem 9.14, Theorem 9.15, and Theorem 9.17 to prove the following theorem.

Theorem 9.18.

The set of all rational numbers is countably infinite.

Proof

Exercise (7) on page 474.

In Section 9.1, we proved that any subset of a finite set is finite (Theorem 9.6). A similar result should be expected for countable sets. We first prove that every subset of is countable. For an infinite subset of , the idea of the proof is to define a function by removing the elements from from smallest to the next smallest to the next smallest, and so on. We do this by defining the function recursively as follows:

• Let be the smallest natural number in .
• Remove from B and let be the smallest natural number in .
• Remove and let be the smallest natural number in .
• We continue this process. The formal recursive definition of is included in the proof of Theorem 9.19.

Theorem 9.19.

Every subset of the natural numbers is countable.

Proof

Let be a subset of . If is finte, then is countable. So we next assume that is infinite. We will next give a recursive definition of a function and then prove that is a bijection.

• Let be the smallest natural number in .
• For each , the set is not empty since is infinte. Define to be the smallest natural number in .

The proof that the function g is a bijection is Exercise (11) on page 475.

Corollary 9.20.

Every subset of a countable set is countable.

Proof

Exercise (12) on page 475.

Exercise 9.2

1. State whether each of the following is true or false.
   
   (a) If a set is countably infinite, then is infinite.
   (b) If a set is countably infinite, then is countable.
   (c) If a set is uncountable, then is not countably infinite.
   (d) If for some , then is not countable.
2. Prove that each of the following sets is countably infinite.
   
   (a) The set of all natural numbers that are multiple of 5
   (b) The set of all integers that are multiples of 5
   (c)
   (d) \{n \in \mathbb{Z}\ |\ n \ge -10\}\)
   (e)
   (f) \(\{m \in \mathbb{Z}\ |\ m \equiv 2\text{ (mod 3)\}\)
3. Prove part (2) of Theorem 9.10.
   Let and be sets. If is infinite and , then is infinite.
4. Complete the proof of Theorem 9.15 by proving the following:
   Let be a countably infinite set and . If is a bijection, then is a bijection, where by
   
5. Prove Theorem 9.16.
   If is a countably infinite set and is a finite set, then is a countably infinite set.

   Hint: Let card() and use a proof by induction on . Theorem 9.15 is the basis step.

6. Complete the proof of Theorem 9.17 by proving the following:
   Let and be disjoint countably infinite sets and let and be bijections. Define by
   
   Then the function is a bijection.
7. Prove Theorem 9.18.
   The set of all rational numbers is countable.
   Hint: Use Theorem 9.15 and Theorem 9.17.
8. Prove that if is countably infinite and is finite, then is countably infinite.
9. Define as follows: For each ,
   
   
   (a) Prove that is an injection. Hint: If , there are three cases to consider: , , and . Use laws of exponents to prove that the first two cases lead to a contradiction.
   (b) Prove that is a surjection. Hint: You may use the fact that if , then , where is an odd natural number and is a nonnegative integer. This is actually a consequence of the Fundamental Theorem of Arithmetic, Theorem 8.15. [See Exercise (13) in Section 8.2.]
   (c) Prove that and hence that card .
10. Use Exercise (9) to prove that if and are countably infinite sets, then is a countably infinite set.
11. Complete the proof of Theorem 9.19 by proving that the function defined in the proof is a bijection from to .

    Hint: To prove that is an injection, it might be easier to prove that for all , if , then . To do this, we may assume that since one of the two numbers must be less than the other. Then notice that .

    To prove that is a surjection, let and notice that for some , there will be natural numbers in that are less than .

12. Prove Corollary 9.20, which states that every subset of a countable set is countable.

    Hint: Let be a countable set and assume that . There are two cases: is finite or is infinite. If is infinite, let be a bijection and define by , for each .

13. Use Corollary 9.20 to prove that the set of all rational numbers between 0 and 1 is countably infinite.
    
    Explorations and Activities
14. Another Proof that Is Countable. For this activity, it may be helpful to use the Fundamental Theorem of Arithmetic (see Theorem 8.15 on page 432). Let be the set of positive rational numbers. Every positive rational number has a unique representation as a fraction , where and are relatively prime natural numbers. We will now define a function as follows:
    
    If and , where , and gcd , we write
    
    where are distinct prime numbers, are distinct prime numbers, and and are natural numbers.
    We also write when . We then define
    
    If , then we define .
    
    (a) Determine , , , , , and .
    (b) If possible, find such that .
    (c) If possible, find such that .
    (d) If possible, find such that .
    (e) Prove that the function is an injection.
    (f) Prove that the function is a surjection.
    (g) What has been proved?

Answer

Add texts here. Do not delete this text first.