1.4: Definitions of Elementary Number Theory
- Page ID
- 19363
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.4.1: Even and Odd
If you divide a number by \(2\) and it comes out even (i.e. with no remainder) the number is said to be even. So the word even is related to division. It turns out that the concept even is better understood through thinking about multiplication.
An integer \(n\) is even exactly when there is an integer \(m\) such that \(n = 2m\).
You should note that there is a “two-way street” sort of quality to this definition – indeed with most, if not all, definitions. If a number is even, then we are guaranteed the existence of another integer half as big. On the other hand, if we can show that another integer half as big exists, then we know the original number is even. This two-wayness means that the definition is what is known as a biconditional, a concept which we’ll revisit in Section 2.2.
A lot of people don’t believe that \(0\) should be counted as an even number. Now that we are armed with a precise definition, we can answer this question easily. Is there an integer \(x\) such that \(0 = 2x\)? Certainly! let \(x\) also be \(0\). (Notice that in the definition, nothing was said about \(m\) and \(n\) being distinct from one another.)
An integer is odd if it isn’t even. That is, amongst integers, there are only two possibilities: even or odd. We can also define oddness without reference to “even.”
An integer \(n\) is odd exactly when there is an integer \(m\) such that \(n = 2m + 1\).
1.4.2: Decimal and Base-\(n\) Notation
You can also identify even numbers by considering their decimal representation. Recall that each digit in the decimal representation of a number has a value that depends on its position. For example, the number \(3482\) really means \(3 · 10^3 + 4 · 10^2 + 8 · 10^1 + 2 · 10^0\). This is also known as place notation. The fact that we use the powers of \(10\) in our place notation is probably due to the fact that most humans have \(10\) fingers. It is possible to use any number in place of \(10\). In Computer Science there are \(3\) other bases in common use: \(2\), \(8\) and \(16\) – these are known (respectively) as binary, octal and hexadecimal notation. When denoting a number using some base other than \(10\), it is customary to append a subscript indicating the base. So, for example, \(1011_2\) is binary notation meaning \(1 · 2^3 + 0 · 2^2 + 1 · 2^1 + 1 · 2^0\) or \(8 + 2 + 1 = 11\). No matter what base we are using, the rightmost digit of the number multiplies the base raised to the \(0\)-th power. Any number raised to the \(0\)-th power is \(1\), and the rightmost digit is consequently known as the units digit. We are now prepared to give some statements that are equivalent to our definition of even. These statements truly don’t deserve the designation “theorem,” they are immediate consequences of the definition.
An integer is even if the units digit in its decimal representation is one of \(0\), \(2\), \(4\), \(6\) or \(8\).
An integer is even if the units digit in its binary representation is \(0\).
For certain problems it is natural to use some particular notational system. For example, the last theorem would tend to indicate that binary numbers are useful in problems dealing with even and odd. Given that there are many different notations that are available to us, it is obviously desirable to have means at our disposal for converting between them. It is possible to develop general rules for converting a base-\(a\) number to a base-\(b\) number (where a and b are arbitrary) but it is actually more convenient to pick a “standard” base (and since we’re human we’ll use base-\(10\)) and develop methods for converting between an arbitrary base and the “standard” one. Imagine that in the not-too-distant future we need to convert some numbers from the base-\(7\) system used by the Seven-lobed Amoebazoids from Epsilon Eridani III to the base-\(12\) scheme favored by the Dodecatons of Alpha-Centauri IV. We will need a procedure for converting base-\(7\) to base-\(10\) and another procedure for converting from base-\(10\) to base-\(12\). In the School House Rock episode “Little Twelve Toes” they describe base-\(12\) numeration in a way that is understandable for elementary school children – the digits they use are \(\{1, 2, 3, 4, 5, 6, 7, 8, 9, δ, \epsilon \}\), the last two digits (which are pronounced “dec” and “el”) are necessary since we need single symbols for the things we ordinarily denote using \(10\) and \(11\).
Converting from some other base to decimal is easy. You just use the definition of place notation. For example, to find what \(451663_7\) represents in decimal, just write
\(4·7^5+5·7^4+1·7^3+6·7^2+6·7+3 = 4·16807+5·2401+1·343+6·49+6·7+3 = 79915.\)
(Everything in the line above can be interpreted as a base-\(10\) number, and no subscripts are necessary for base-\(10\).)
Converting from decimal to some other base is harder. There is an algorithm called “repeated division” that we’ll explore a bit in the exercises for this section. For the moment, just verify that \(3δ2 \epsilon 7_{12}\) is also a representation of the number more conventionally written as \(79915\).
1.4.3: Divisibility
The notion of being even has an obvious generalization. Suppose we asked whether \(3\) divided evenly into a given number. Presumably, we could make a definition of what it meant to be threeven, but rather than doing so (or engaging in any further punnery) we shall instead move to a general definition. We need a notation for the situation when one number divides evenly into another. There are many ways to describe this situation in English, but essentially just one in “math,” we use a vertical bar – not a fraction bar. Indeed the difference between this vertical bar and the fraction symbol (\(|\) versus \(/\)) needs to be strongly stressed. The vertical bar when placed between two numbers is a symbol which asks the question “Does the first number divide evenly (i.e. with no remainder) into the second?” On the other hand the fraction bar asks you to actually carry out some division. The value of \(2 | 5\) is false, whereas the value of \(2/5\) is \(.4\).
As was the case in defining even, it turns out that it is best to think of multiplication, not division, when making a formal definition of this concept. Given any two integers \(n\) and \(d\) we define the symbol \(d|n\) by
\(d|n\) exactly when \(∃k ∈ Z\) such that \(n = kd\)
In spoken language the symbol \(d|n\) can be translated in a variety of ways:
- \(d\) is a divisor of \(n\).
- \(d\) divides \(n\) evenly.
- \(d\) is a factor of \(n\).
- \(n\) is an integer multiple of \(d\).
Although, by far the most popular way of expressing this concept is to just say “\(d\) divides \(n\).”
1.4.4: Floor and Ceiling
Suppose there is an elevator with a capacity of \(1300\) pounds. A large group of men who all weigh about \(200\) pounds want to ascend in it. How many should ride at a time? This is just a division problem, \(1300/200\) gives \(6.5\) men should ride together. Well, obviously putting half a person on an elevator is a bad idea – should we just round-up and let \(7\) ride together? Not if the \(1300\) pound capacity rating doesn’t have a safety margin! This is an example of the kind of problem in which the floor function is used. The floor function takes a real number as input and returns the next lower integer.
Suppose after a party we have \(43\) unopened bottles of beer. We’d like to store them in containers that hold \(12\) bottles each. How many containers will we need? Again, this is simply a division problem \(– 43/12 = 3.58333\). So we need \(3\) boxes and another \(7\) twelfths of a box. Obviously, we really need \(4\) boxes – at least one will have some unused space in it. In this sort of situation, we’re dealing with the ceiling function. Given a real number, the ceiling function rounds it up to the next integer.
Both of these functions are denoted using symbols that look very much like absolute value bars. The difference lies in some small horizontal strokes.
If \(x\) is a real number, its floor is denoted \(\lfloor x \rfloor\), and its ceiling is denoted \(\lceil x \rceil\). Here are the formal definitions:
\(y = \lfloor x \rfloor\) exactly when \(y ∈ Z\) and \(y ≤ x < y + 1\).
\(y = \lceil x \rceil\) exactly when \(y ∈ Z\) and \(y − 1 < x ≤ y\).
Basically, the definition of floor says that \(y\) is an integer that is less than or equal to \(x\), but \(y + 1\) definitely exceeds \(x\). The definition of ceiling can be paraphrased similarly.
1.4.5: Div and mod
In the next section, we’ll discuss the so-called division algorithm – this may be over-kill since you certainly already know how to do division! Indeed, in the U.S., long division is usually first studied in the latter half of elementary school, and division problems that don’t involve a remainder may be found as early as the first grade. Nevertheless, we’re going to discuss this process in sordid detail because it gives us a good setting in which to prove relatively easy statements. Suppose you are setting-up a long division problem in which the integer \(n\) is being divided by a positive divisor \(d\). (If you want to divide by a negative number, just divide by the corresponding positive number and then throw an extra minus sign on at the end.)
\( \;\;\;\underline{\;\;q\;\;\;} \\ d| \;\;n \\ \;\;\;\;... \\ \;\;\underline{\;\;\;\;\;\;\;\;} \\ \;\;\;\;\;r\)
Recall that the answer consists of two parts, a quotient \(q\), and a remainder \(r\). Of course, \(r\) may be zero, but also, the largest \(r\) can be is \(d − 1\). The assertion that this answer uniquely exists is known as the quotient-remainder theorem:
Given integers \(n\) and \(d > 0\), there are unique integers \(q\) and \(r\) such that \(n = qd + r\) and \(0 ≤ r < d\).
The words “div” and “mod” that appear in the title of this subsection provide mathematical shorthand for \(q\) and \(r\). Namely, “\(n \text{ mod } d\)” is a way of expressing the remainder \(r\), and “\(n \text{ div } d\)” is a way of expressing the quotient \(q\).
If two integers, \(m\) and \(n\), leave the same remainder when you divide them by \(d\), we say that they are congruent modulo \(d\). One could express this by writing \(n \text{ mod } d = m \text{ mod } d \), but usually we adopt a shorthand notation
\[n ≡ m (\text{mod } d).\]
If one is in a context in which it is completely clear what \(d\) is, it’s acceptable to just write \(n ≡ m\).
The “\(\text{mod}\)” operation is used quite a lot in mathematics. When we do computations modulo some number\(d\), (this is known as “modular arithmetic” or, sometimes, “clock arithmetic”) some very nice properties of “\(\text{mod}\)” come in handy
\[x + y \text{ mod } d = (x \text{ mod } d + y \text{ mod } d) \text{ mod } d\]
and
\[x · y \text{ mod } d = (x \text{ mod } d · y \text{ mod } d) \text{ mod } d.\]
These rules mean that we can either do the operations first, then reduce the answer \(\text{mod } d\) or we can do the reduction \(\text{mod } d\) first and then do the operations (although we may have to do one more round of reduction \(\text{mod } d\)).
For example, if we are working \(\text{mod } 10\), and want to compute \(87·96 \text{ mod } 10\), we can instead just compute \(7 · 6 \text{ mod } 10\), which is \(2\).
1.4.6: Binomial Coefficients
A “binomial” is a polynomial with \(2\) terms, for example \(x + 1\) or \(a + b\). The numbers that appear as the coefficients when one raises a binomial to some power are – rather surprisingly – known as binomial coefficients
Let’s have a look at the first several powers of \(a + b\).
\[\begin{array} (a + b)^0 &= 1 \\ (a + b)^1 &= a + b \\ (a + b)^2 &= a^2 + 2ab + b^2 \end{array}\]
To go much further than the second power requires a bit of work, but try the following
Multiply \((a+b)\) and \((a^2 + 2ab+b^2)\) in order to determine \((a+b)^3\). If you feel up to it, multiply \((a^2+2ab+b^2)\) times itself in order to find \((a+b)^4\).
Since we’re interested in the coefficients of these polynomials, it’s important to point out that if no coefficient appears in front of a term that means the coefficient is \(1\).
These binomial coefficients can be placed in an arrangement known as Pascal’s triangle1, which provides a convenient way to calculate small binomial coefficients
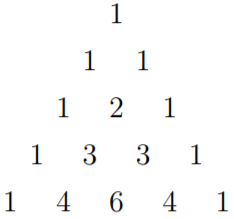
Notice that in the triangle there is a border on both sides containing 1’s and that the numbers on the inside of the triangle are the sum of the two numbers above them. You can use these facts to extend the triangle.
Add the next two rows to the Pascal triangle in Figure \(1.4.1\).
Binomial coefficients are denoted using a somewhat strange-looking symbol. The number in the \(k\)-th position in row number \(n\) of the triangle is denoted \(\binom{n}{k}\). This looks a little like a fraction, but the fraction bar is missing. Don’t put one in! It’s supposed to be missing. In spoken English, you say “\(n\) choose \(k\)” when you encounter the symbol \(\binom{n}{k}\).
There is a formula for the binomial coefficients – which is nice. Otherwise we’d need to complete a pretty huge Pascal triangle in order to compute something like \(\binom{52}{5}\). The formula involves factorial notation. Just to be sure we are all on the same page, we’ll define factorials before proceeding.
The symbol for factorials is an exclamation point following a number. This is just a short-hand for expressing the product of all the numbers up to a given one. For example \(7!\) means \(1 · 2 · 3 · 4 · 5 · 6 · 7\). Of course, there’s really no need to write the initial \(1\) — also, for some reason people usually write the product in decreasing order \((7! = 7 · 6 · 5 · 4 · 3 · 2)\).
The formula for a binomial coefficient is
\[\binom{n}{k} = \dfrac{n!}{k! · (n − k)!} \]
For example
\[\binom{5}{3} = \dfrac{5!}{3! · (5 − 3)!} = \dfrac{1 · 2 · 3 · 4 · 5}{ (1 · 2 · 3) · (1 · 2)} = 10 \]
A slightly more complicated example (and one that gamblers are fond of) is
\[\begin{array} \binom{52}{5} &= \dfrac{52!}{5! · (52 − 5)!} \\ &= \dfrac{1 · 2 · 3 · · · · 52}{(1 · 2 · 3 · 4 · 5) · (1 · 2 · 3 · · · · 47)} \\ &= \dfrac{48 · 49 · 50 · 51 · 52}{1 · 2 · 3 · 4 · 5} \\ &= 2598960. \end{array}\]
The reason that a gambler might be interested in the number we just calculated is that binomial coefficients do more than just give us the coefficients in the expansion of a binomial. They also can be used to compute how many ways one can choose a subset of a given size from a set. Thus \(\binom{52}{5}\) is the number of ways that one can get a \(5\) card hand out of a deck of \(52\) cards.
There are seven days in a week. In how many ways can one choose a set of three days (per week)
Exercises:
An integer \(n\\) is doubly-even if it is even, and the integer \(m\) guaranteed to exist because \(n\) is even is itself even. Is \(0\) doubly-even? What are the first \(3\) positive, doubly-even integers?
Dividing an integer by two has an interesting interpretation when using binary notation: simply shift the digits to the right. Thus, \(22 = 10110_2\) when divided by two gives \(1011_2\) which is \(8 + 2 + 1 = 11\). How can you recognize a doubly-even integer from its binary representation?
The octal representation of an integer uses powers of \(8\) in place notation. The digits of an octal number run from \(0\) to \(7\), one never sees \(8\)’s or \(9\)’s. How would you represent \(8\) and \(9\) as octal numbers? What octal number comes immediately after \(777_8\)? What (decimal) number is \(777_8\)?
One method of converting from decimal to some other base is called repeated division. One divides the number by the base and records the remainder – one then divides the quotient obtained by the base and records the remainder. Continue dividing the successive quotients by the base until the quotient is smaller than the base. Convert \(3267\) to base-\(7\) using repeated division. Check your answer by using the meaning of base-\(7\) place notation. (For example \(54321_7\) means \(5 · 7^4 + 4 · 7^3 + 3 · 7^2 + 2 · 7^1 + 1 · 7^0\).)
State a theorem about the octal representation of even numbers.
In hexadecimal (base-\(16\)) notation one needs \(16\) “digits,” the ordinary digits are used for \(0\) through \(9\), and the letters \(\text{A}\) through \(\text{F}\) are used to give single symbols for \(10\) through \(15\). The first \(32\) natural number in hexadecimal are:
\(1,2,3,4,5,6,7,8,9,\text{A},\text{B},\text{C},\text{D},\text{E},\text{F},10,11,12,13,14,15,16,17,18,19,1\text{A},1\text{B},1\text{C},1\text{D},1\text{E},1\text{F},20\).
Write the next \(10\) hexadecimal numbers after \(\text{AB}\).
For conversion between the three bases used most often in Computer Science we can take binary as the “standard” base and convert using a table look-up. Each octal digit will correspond to a binary triple, and each hexadecimal digit will correspond to a \(4\)-tuple of binary numbers. Complete the following tables. (As a check, the \(4\)-tuple next to \(A\) in the table for hexadecimal should be \(1010\) – which is nice since \(A\) is really \(10\) so if you read that as “ten-ten” it is a good aid to memory.)
| octal | binary |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
| hexadecimal | binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| \(\text{A}\) | |
| \(\text{B}\) | |
| \(\text{C}\) | |
| \(\text{D}\) | |
| \(\text{E}\) | |
| \(\text{F}\) |
Use the tables from the previous problem to make the following conversions.
- Convert \(757_8\) to binary.
- Convert \(1007_8\) to hexadecimal.
- Convert \(100101010110_2\) to octal.
- Convert \(1111101000110101_2\) to hexadecimal.
- Convert \(FEED_{16}\) to binary.
- Convert \(FFFFFF_{16}\) to octal.
Try the following conversions between various number systems:
- Convert \(30\) (base \(10\)) to binary.
- Convert \(69\) (base \(10\)) to base \(5\).
- Convert \(12223\) to binary.
- Convert \(12347\) to base \(10\).
- Convert \(EEED_{15}\) to base \(12\). (Use \(\{1, 2, 3 . . . 9, d, e\}\) as the digits in base \(12\).)
- Convert \(6789\) to hexadecimal.
It is a well known fact that if a number is divisible by \(3\), then \(3\) divides the sum of the (decimal) digits of that number. Is this result true in base \(7\)? Do you think this result is true in any base?
Suppose that \(340\) pounds of sand must be placed into bags having a \(50\) pound capacity. Write an expression using either floor or ceiling notation for the number of bags required.
True or false?
\(\lfloor \dfrac{n}{d} \rfloor < \lceil \dfrac{n}{d} \rceil \)
for all integers \(n\) and \(d > 0\). Support your claim.
What is the value of \(\lceil π \rceil^2 − \lceil π^2 \rceil\)?
Assuming the symbols \(n\), \(d\), \(q\) and \(r\) have meanings as in the quotient-remainder theorem (Theorem \(1.4.3\)). Write expressions for \(q\) and \(r\), in terms of \(n\) and \(d\) using floor and/or ceiling notation.
Calculate the following quantities:
- \(3 \text{ mod } 5\)
- \(37 \text{ mod } 7\)
- \(1000001 \text{ mod } 100000\)
- \(6 \text{ div } 6\)
- \(7 \text{ div } 6\)
- \(1000001 \text{ div } 2\)
Calculate the following binomial coefficients:
- \(\binom{3}{0}\)
- \(\binom{7}{7}\)
- \(\binom{13}{5}\)
- \(\binom{13}{8}\)
- \(\binom{52}{7}\)
An ice cream shop sells the following flavors: chocolate, vanilla, strawberry, coffee, butter pecan, mint chocolate chip and raspberry. How many different bowls of ice cream – with three scoops – can they make?


