3.6: Proofs and Disproofs of Existential Statements
( \newcommand{\kernel}{\mathrm{null}\,}\)
From a certain point of view, there is no need for the current section. If we are proving an existential statement we are disproving some universal statement. (Which has already been discussed.) Similarly, if we are trying to disprove an existential statement, then we are actually proving a related universal statement. Nevertheless, sometimes the way a theorem is stated emphasizes the existence question over the corresponding universal – and so people talk about proving and disproving existential statements as a separate issue from universal statements.
Proofs of existential questions come in two basic varieties: constructive and non-constructive. Constructive proofs are conceptually the easier of the two – you actually name an example that shows the existential question is true. For example:
There is an even prime.
- Proof
-
The number 2 is both even and prime.
Q.E.D.
The Fibonacci numbers are defined by the initial values F(0)=1 and F(1)=1 and the recursive formula F(n+1)=F(n)+F(n−1) (to get the next number in the series you add the last and the penultimate).
| n | F(n) |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 8 |
| ⋮ | ⋮ |
Prove that there is a Fibonacci number that is a perfect square.
A non-constructive existence proof is trickier. One approach is to argue by contradiction – if the thing we’re seeking doesn’t exist that will lead to an absurdity. Another approach is to outline a search algorithm for the desired item and provide an argument as to why it cannot fail!
A particularly neat approach is to argue using dilemma. This is my favorite non-constructive existential theorem/proof.
There are irrational numbers α and β such that α^β is rational.
- Proof
-
If \sqrt{2}^{\sqrt{2}} is rational then we are done. (Let α = β = \sqrt{2}.) Otherwise, let α = \sqrt{2}^{\sqrt{2}} and β = \sqrt{2}. The result follows because \left( \sqrt{2}^{\sqrt{2}} \right)^{\sqrt{2}} = \sqrt{2}^{(\sqrt{2}\sqrt{2})} = \sqrt{2}^{2} = 2, which is clearly rational.
Q.E.D.
Many existential proofs involve a property of the natural numbers known as the well-ordering principle. The well-ordering principle is sometimes abbreviated WOP. If a set has WOP it doesn’t mean that the set is ordered in a particularly good way, but rather that its subsets are like wells – the kind one hoists water out of with a bucket on a rope. You needn’t be concerned with WOP in general at this point, but notice that the subsets of the natural numbers have a particularly nice property – any non-empty set of natural numbers must have a least element (much like every water well has a bottom).
Because the natural numbers have the well-ordering principle we can prove that there is a least natural number with property \text{X} by simply finding any natural number with property \text{X} – by doing that we’ve shown that the set of natural numbers with property \text{X} is non-empty and that’s the only hypothesis the WOP needs.
For example, in the exercises in Section 3.5 we introduced vampire numbers. A vampire number is a 2n digit number v that factors as v = xy where x and y are n digit numbers and the digits of v are precisely the digits in x and y in some order. The numbers x and y are known as the “fangs” of v. To eliminate trivial cases, both fangs may not end with zeros.
There is a smallest 6-digit vampire number.
- Proof
-
The number 125460 is a vampire number (in fact this is the smallest example of a vampire number with two sets of fangs: 125460 = 204 · 615 = 246 · 510). Since the set of 6-digit vampire numbers is non-empty, the well-ordering principle of the natural numbers allows us to deduce that there is a smallest 6-digit vampire number.
Q.E.D.
This is quite an interesting situation in that we know there is a smallest 6-digit vampire number without having any idea what it is!
Show that 102510 is the smallest 6-digit vampire number.
There are quite a few occasions when we need to prove statements involving the unique existence quantifier (∃!). In such instances, we need to do just a little bit more work. We need to show existence – either constructively or non-constructively – and we also need to show uniqueness. To give an example of a unique existence proof we’ll return to a concept first discussed in Section 1.5 and finish-up some business that was glossed-over there.
Recall the Euclidean algorithm that was used to calculate the greatest common divisor of two integers a and b (which we denote \text{gcd}(a, b)). There is a rather important question concerning algorithms known as the “halting problem.” Does the program eventually halt, or does it get stuck in an infinite loop? We know that the Euclidean algorithm halts (and outputs the correct result) because we know the following unique existence result.
∀a, b ∈ \mathbb{Z} +, ∃! d ∈ \mathbb{Z}^+ such that d = \text{gcd}(a, b)
Now, before we can prove this result, we’ll need a precise definition for \text{gcd}(a, b). Firstly, a \text{gcd} must be a common divisor which means it needs to divide both a and b. Secondly, among all the common divisors, it must be the largest. This second point is usually addressed by requiring that every other common divisor divides the \text{gcd}. Finally, we should note that a \text{gcd} is always positive, for whenever a number divides another number so does its negative, and whichever of those two is positive will clearly be the greater! This allows us to extend the definition of \text{gcd} to all integers, but things are conceptually easier if we keep our attention restricted to the positive integers.
The greatest common divisor, or gcd, of two positive integers a and b is a positive integer d such that d | a and d | b and if c is any other positive integer such that c |a and c | b then c |d.
∀a, b, c, d ∈ \mathbb{Z}^+ d = \text{gcd}(a, b) \iff d|a ∧ d| b ∧ (c |a ∧ c | b \implies c |d)
Armed with this definition, let’s return our attention to proving the unique existence of the \text{gcd}. The uniqueness part is easier so we’ll do that first. We argue by contradiction. Suppose that there were two different numbers d and d' satisfying the definition of \text{gcd}(a, b). Put d' in the place of c in the definition to see that d' | d. Similarly, we can deduce that d | d' and if two numbers each divide into the other, they must be equal. This is a contradiction since we assumed d and d' were different.
For the existence part, we’ll need to define a set – known as the \mathbb{Z}-module generated by a and b – that consists of all numbers of the form xa+yb where x and y range over the integers.
This set has a very nice geometric character that often doesn’t receive the attention it deserves. Every element of a \mathbb{Z}-module generated by two numbers (15 and 21 in the example) corresponds to a point in the Euclidean plane. As indicated in Figure 3.6.1 there is a dividing line between the positive and negative elements in a \mathbb{Z}-module. It is also easy to see that there are many repetitions of the same value at different points in the plane.
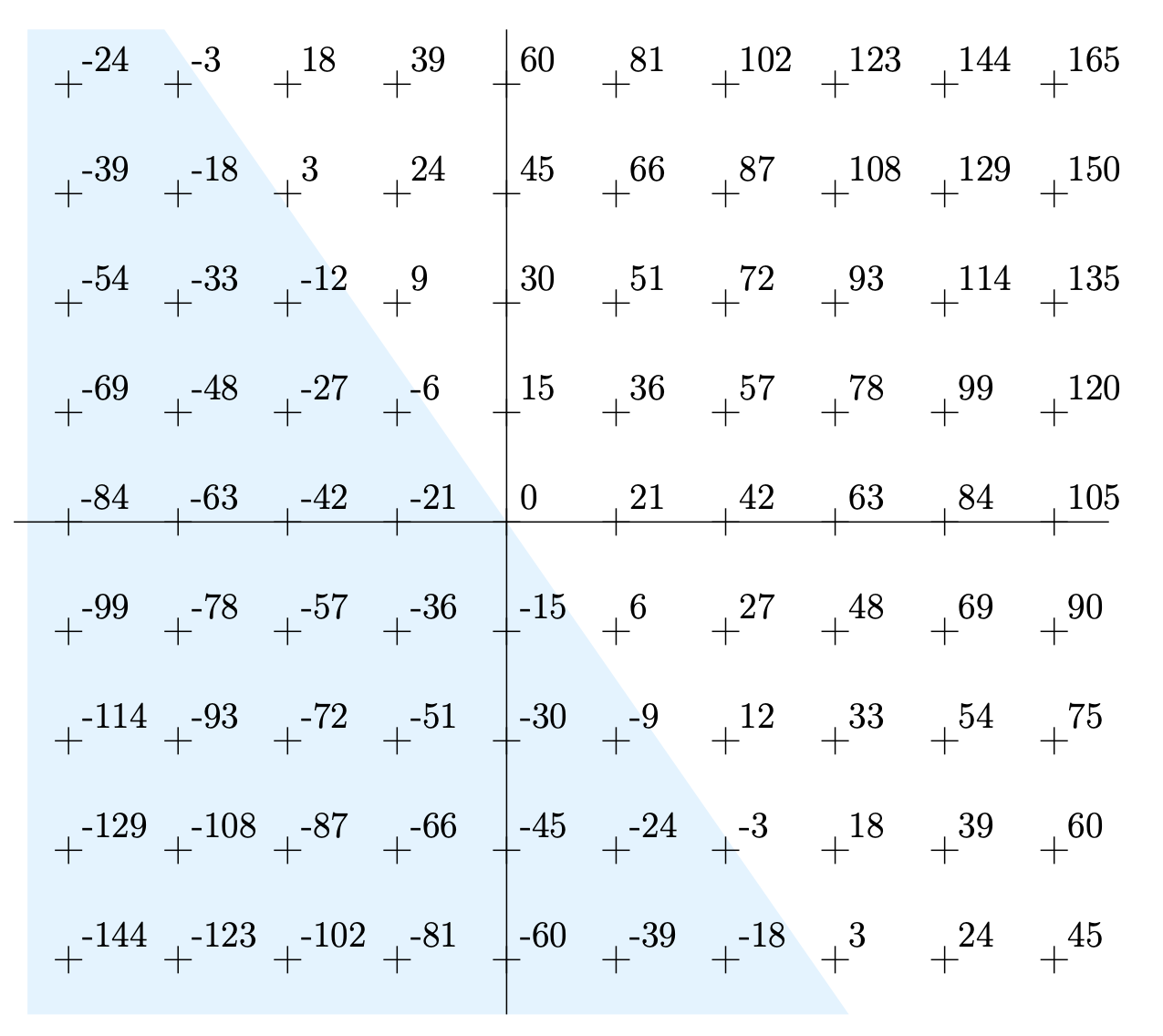
The value 0 clearly occurs in a \mathbb{Z}-module when both x and y are themselves zero. Find another pair of (x, y) values such that 21x + 15y is zero. What is the slope of the line which separates the positive values from the negative in our \mathbb{Z}-module?
In thinking about this \mathbb{Z}-module, and perusing Figure 3.6.1, you may have noticed that the smallest positive number in the \mathbb{Z}-module is 3. If you hadn’t noticed that, look back and verify that fact now.
How do we know that some smaller positive value (a 1 or a 2) doesn’t occur somewhere in the Euclidean plane?
What we’ve just observed is a particular instance of a general result.
The smallest positive number in the \mathbb{Z}-module generated by a and b is d = \text{gcd}(a, b).
- Proof
-
Suppose that d is the smallest positive number in the Zmodule \{xa+yb x, y ∈ \mathbb{Z}\}. There are particular values of x and y (which we will distinguish with over-lines) such that d = xa + yb. Now, it is easy to see that if c is any common divisor of a and b then c |d, so what remains to be proved is that d itself is a divisor of both a and b. Consider dividing d into a. By the division algorithm, there are uniquely determined numbers q and r such that a = qd+r with 0 ≤ r < d. We will show that r = 0. Suppose, to the contrary, that r is positive. Note that we can write r as r = a − qd = a − q(\overline{x}a + \overline{y}b) = (1 − q \overline{x})a − q \overline{y}b. The last equality shows that r is in the \mathbb{Z}-module under consideration, and so, since d is the smallest positive integer in this \mathbb{Z}-module it follows that r ≥ d which contradicts the previously noted fact that r < d. Thus, r = 0 and so it follows that d | a. An entirely analogous argument can be used to show that d| b which completes the proof that d = \text{gcd}(a, b).
Q.E.D.
Exercises:
Show that there is a perfect square that is the sum of two perfect squares.
Show that there is a perfect cube that is the sum of three perfect cubes.
Show that the WOP doesn’t hold in the integers. (This is an existence proof, you show that there is a subset of \mathbb{Z} that doesn’t have a smallest element.)
Show that the WOP doesn’t hold in \mathbb{Q}^+.
In the proof of Theorem 3.6.3 we weaseled out of showing that d | b. Fill in that part of the proof.
Give a proof of the unique existence of q and r in the division algorithm.
A digraph is a drawing containing a collection of points that are connected by arrows. The game known as scissors-paper-rock can be represented by a digraph that is balanced (each point has the same number of arrows going out as going in). Show that there is a balanced digraph having 5 points.