8.4: Dominance
- Page ID
- 19412
We’ve said a lot about the equivalence relation determined by Cantor’s definition of set equivalence. We’ve also, occasionally, written things like \(|A| < |B|\), without being particularly clear about what that means. It’s now time to come clean. There is actually a (perhaps) more fundamental notion used for comparing set sizes than equivalence — dominance. Dominance is an ordering relation on the class of all sets. One should probably really define dominance first and then define set equivalence in terms of it. We haven’t followed that plan for (at least) two reasons. First, many people may want to skip this section — the results of this section depend on the difficult Cantor-Bernstein-Schröder theorem1. Second, we will later take the view that dominance should really be considered to be an ordering relation on the set of all cardinal numbers – i.e. the equivalence classes of the set equivalence relation – not on the collection of all sets. From that perspective, set equivalence really needs to be defined before dominance.
One set is said to dominate another if there is a function from the latter into the former. More formally, we have the following
If A and B are sets, we say “\(A\) dominates \(B\)” and write \(|A| > |B|\) iff there is an injective function \(f\) with domain \(B\) and codomain \(A\).
It is easy to see that this relation is reflexive and transitive. The Cantor-Bernstein-Schröder theorem proves that it is also anti-symmetric — which means dominance is an ordering relation. Be advised that there is an abuse of terminology here that one must be careful about — what are the domain and range of the “dominance” relation? The definition would lead us to think that sets are the things that go on either side of the “dominance” relation, but the notation is a bit more honest, “\(|A| > |B|\)” indicates that the things really being compared are the cardinal numbers of sets (not the sets themselves). Thus anti-symmetry for this relation is
\[(|A| > |B|) ∧ (|B| > |A|) \implies (|A| = |B|).\]
In other words, if \(A\) dominates \(B\) and vice versa, then \(A\) and \(B\) are equivalent sets — a strict interpretation of anti-symmetry for this relation might lead to the conclusion that \(A\) and \(B\) are actually the same set, which is clearly an absurdity.
Naturally, we want to prove the Cantor-Bernstein-Schröder theorem (which we’re going to start calling the C-B-S theorem for brevity), but first it’ll be instructive to look at some of its consequences. Once we have the C-B-S theorem we get a very useful shortcut for proving set equivalences. Given sets \(A\) and \(B\), if we can find injective functions going between them in both directions, we’ll know that they’re equivalent. So, for example, we can use C-B-S to prove that the set of all infinite binary strings and the set of reals in \((0, 1)\) really are equinumerous. (In case you had some remaining doubt. . . )
It is easy to dream up an injective function from \((0, 1)\) to \(\mathbb{F}^∞_2\): just send a real number to its binary expansion, and if there are two, make a consistent choice — let’s say we’ll take the non-terminating expansion.
There is a cute thought-experiment called Hilbert’s Hotel that will lead us to a technique for developing an injective function in the other direction. Hilbert’s Hotel has \(ℵ_0\) rooms. If any countable collection of guests show up there will be enough rooms for everyone. Suppose you arrive at Hilbert’s hotel one dark and stormy evening and the “No Vacancy” light is on — there are already a denumerable number of guests there — every room is full. The clerk sees you dejectedly considering your options, trying to think of another hotel that might still have rooms when, clearly, a very large convention is in town. He rushes out and says “My friend, have no fear! Even though we have no vacancies, there is always room for one more at our establishment.” He goes into the office and makes the following announcement on the PA system. “Ladies and Gentlemen, in order to accommodate an incoming guest, please vacate your room and move to the room numbered one higher. Thank you.” There is an infinite amount of grumbling, but shortly you find yourself occupying room number \(1\).
To develop an injection from \(\mathbb{F}^∞_2\) to \((0, 1)\) we’ll use “room number \(1\)” to separate the binary expansions that represent the same real number. Move all the digits of a binary expansion down by one, and make the first digit \(0\) for (say) the terminating expansions and \(1\) for the non-terminating ones. Now consider these expansions as real numbers — all the expansions that previously coincided are now separated into the intervals \(\left(0, \dfrac{1}{2} \right)\) and \(\left(\dfrac{1}{2}, 1\right)\). Notice how funny this map is, there are now many, many, (infinitely-many) real numbers with no preimages. For instance, only a subset of the rational numbers in \(\left(0, \dfrac{1}{2} \right)\) have preimages. Nevertheless, the map is injective, so C-B-S tells us that \(\mathbb{F}^∞_2\) and \((0, 1)\) are equivalent. There are quite a few different proofs of the C-B-S theorem. The one Cantor himself wrote relies on the axiom of choice. The axiom of choice was somewhat controversial when it was introduced, but these days most mathematicians will use it without qualms. What it says (essentially) is that it is possible to make an infinite number of choices. More precisely, it says that if we have an infinite set consisting of non-empty sets, it is possible to select an element out of each set. If there is a definable rule for picking such an element (as is the case, for example, when we selected the nonterminating decimal expansion whenever there was a choice in defining the injection from \((0, 1)\) to \(\mathbb{F}^∞_2\)) the axiom of choice isn’t needed. The usual axioms for set theory were developed by Zermelo and Frankel, so you may hear people speak of the ZF axioms. If, in addition, we want to specifically allow the axiom of choice, we are in the ZFC axiom system. If it’s possible to construct a proof for a given theorem without using the axiom of choice, almost everyone would agree that that is preferable. On the other hand, a proof of the C-B-S theorem, which necessarily must be able to deal with uncountably infinite sets, will have to depend on some sort of notion that will allow us to deal with huge infinities.
The proof we will present here2 is attributed to Julius König. König was a contemporary of Cantor’s who was (initially) very much respected by him. Cantor came to dislike König after the latter presented a well-publicized (and ultimately wrong) lecture claiming the continuum hypothesis was false. Apparently, the continuum hypothesis was one of Cantor’s favorite ideas, because he seems to have construed König’s lecture as a personal attack. Anyway. . .
König’s proof of C-B-S doesn’t use the axiom of choice, but it does have its own strangeness: a function that is not necessarily computable — that is, a function for which (for certain inputs) it may not be possible to compute an output in a finite amount of time! Except for this oddity, König’s proof is probably the easiest to understand of all the proofs of C-B-S. Before we get too far into the proof it is essential that we understand the basic setup. The Cantor-Bernstein-Schröder theorem states that whenever \(A\) and \(B\) are sets and there are injective functions \(f : A \implies B\) and \(g : B \implies A\), then it follows that \(A\) and \(B\) are equivalent. Saying \(A\) and \(B\) are equivalent means that we can find a bijective function between them. So, to prove C-B-S, we hypothesize the two injections and somehow we must construct the bijection.
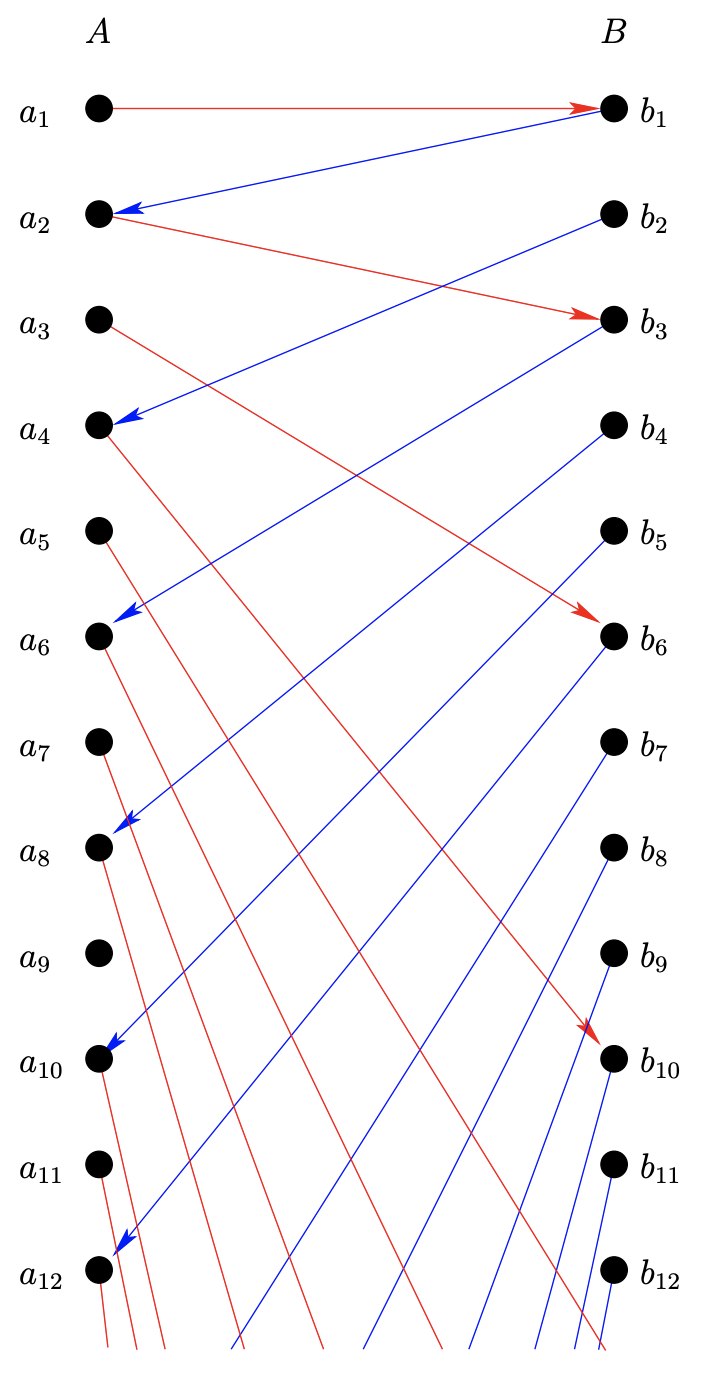
Figure \(8.4.1.\) has a presumption in it — that \(A\) and \(B\) are countable — which need not be the case. Nevertheless, it gives us a good picture to work from. The basic hypotheses, that \(A\) and \(B\) are sets and we have two functions, one from \(A\) into \(B\) and another from \(B\) into \(A\), are shown. We will have to build our bijective function in a piecewise manner. If there is a non-empty intersection between \(A\) and \(B\), we can use the identity function for that part of the domain of our bijection. So, without loss of generality, we can presume that \(A\) and \(B\) are disjoint. We can use the functions \(f\) and \(g\) to create infinite sequences, which alternate back and forth between \(A\) and \(B\), containing any particular element. Suppose \(a ∈ A\) is an arbitrary element. Since \(f\) is defined on all of \(A\), we can compute \(f(a)\). Now since \(f(a)\) is an element of \(B\), and \(g\) is defined on all of \(B\), we can compute \(g(f(a))\), and so on. Thus, we get the infinite sequence
\(a, f(a), g(f(a)), f(g(f(a))), . . .\)
If the element \(a\) also happens to be the image of something under \(g\) (this may or may not be so — since \(g\) isn’t necessarily onto) then we can also extend this sequence to the left. Indeed, it may be possible to extend the sequence infinitely far to the left, or, this process may stop when one of \(f^{−1}\) or \(g^{−1}\) fails to be defined.
\(. . . g^{−1} (f^{−1} (g^{−1} (a))), f^{−1} (g^{−1} (a)), g^{−1} (a), a, f(a), g(f(a)), f(g(f(a))), . . .\)
Now, every element of the disjoint union of \(A\) and \(B\) is in one of these sequences. Also, it is easy to see that these sequences are either disjoint or identical. Taking these two facts together it follows that these sequences form a partition of \(A ∪ B\). We’ll define a bijection \(\phi : A \implies B\) by deciding what it must do on these sequences. There are four possibilities for how the sequences we’ve just defined can play out. In extending them to the left, we may run into a place where one of the inverse functions needed isn’t defined — or not. We say a sequence is an \(A\)-stopper, if, in extending to the left, we end up on an element of \(A\) that has no preimage under \(g\) (see Figure \(8.4.2\)). Similarly, we can define a \(B\)-stopper. If the inverse functions are always defined within a given sequence there are also two possibilities; the sequence may be finite (and so it must be cyclic in nature) or the sequence may be truly infinite.
Finally, here is a definition for \(\phi\).
\( \phi(x)=\left\{ \begin{array}{ll} g^{−1}(x) \;\;\;\;\text{ if } x \text{ is in a } B\text{-stopper}\\ f(x) \;\;\;\;\;\;\;\text{ otherwise} \end{array} \right.\)
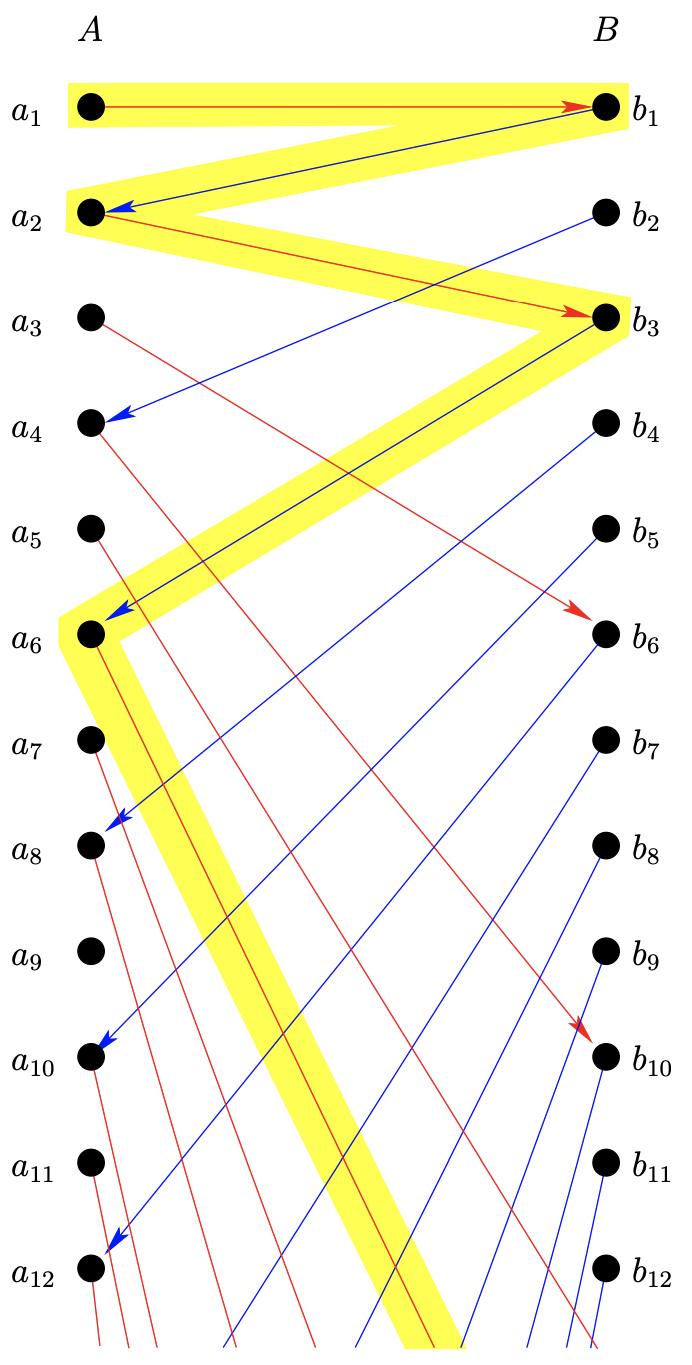
Notice that if a sequence is either cyclic or infinite it doesn’t matter whether we use \(f\) or \(g^{−1}\) since both will be defined for all elements of such sequences. Also, certainly \(f\) will work if we are in an \(A\)-stopper. The function we’ve just created is perfectly well-defined, but it may take arbitrarily long to determine whether we have an element of a \(B\)-stopper, as opposed to an element of an infinite sequence. We cannot determine whether we’re in an infinite versus a finite sequence in a prescribed finite number of steps.
Exercises:
How could the clerk at the Hilbert Hotel accommodate a countable number of new guests?
Let \(F\) be the collection of all real-valued functions defined on the real line. Find an injection from \(\mathbb{R}\) to \(F\). Do you think it is possible to find an injection going the other way? In other words, do you think that \(F\) and \(\mathbb{R}\) are equivalent? Explain.
Fill in the details of the proof that dominance is an ordering relation. (You may simply cite the C-B-S theorem in proving anti-symmetry.)
We can inject \(\mathbb{Q}\) into \(\mathbb{Z}\) by sending \(± \dfrac{a}{b}\) to \(±2^a 3^b\). Use this and another obvious injection to (in light of the C-B-S theorem) reaffirm the equivalence of these sets.


