8.3: Cantor’s Theorem
- Page ID
- 19411
Many people believe that the result known as Cantor’s theorem says that the real numbers, \(\mathbb{R}\), have a greater cardinality than the natural numbers, \(\mathbb{N}\). That isn’t quite right. In fact, Cantor’s theorem is a much broader statement, one of whose consequences is that \(|\mathbb{R}| > |\mathbb{N}|\). Before we go on to discuss Cantor’s theorem in full generality, we’ll first explore it, essentially, in this simplified form. Once we know that \(|\mathbb{R}| \neq |\mathbb{N}|\), we’ll be in a position to explore a lot of interesting issues relative to the infinite. In particular, this result means that there are at least two cardinal numbers that are infinite – thus the “infinity is infinity” idea will be discredited. Once we have the full power of Cantor’s theorem, we’ll see just how completely wrong that concept is.
To show that some pair of sets are not equivalent it is necessary to show that there cannot be a one-to-one correspondence between them. Ordinarily, one would try to argue by contradiction in such a situation. That is what we’ll need to do to show that the reals and the naturals are not equinumerous. We’ll presume that they are in fact the same size and try to reach a contradiction.
What exactly does the assumption that \(\mathbb{R}\) and \(\mathbb{N}\) are equivalent mean? It means there is a one-to-one correspondence, that is, a bijective function from \(\mathbb{R}\) to \(\mathbb{N}\). In a nutshell, it means that it is possible to list all the real numbers in a singly-infinite list. Now, it is certainly possible to make an infinite list of real numbers (since \(\mathbb{N} ⊆ \mathbb{R}\), by listing the naturals themselves we are making an infinite list of reals!). The problem is that we would need to be sure that every real number is on the list somewhere. In fact, since we’ve used a geometric argument to show that the interval \((0, 1)\) and the set \(\mathbb{R}\) are equinumerous, it will be sufficient to presume that there is an infinite list containing all the numbers in the interval \((0, 1)\).
Notice that, for example, \(π − 3\) is a real number in \((0, 1)\). Make a list of \(10\) real numbers in the interval \((0, 1)\). Make sure that at least \(5\) of them are not rational.
In the previous exercise, you’ve started the job, but we need to presume that it is truly possible to complete this job. That is, we must presume that there really is an infinite list containing every real number in the interval \((0, 1)\).
Once we have an infinite list containing every real number in the interval \((0, 1)\) we have to face up to a second issue. What does it really mean to list a particular real number? For instance, if \(e − 2\) is in the seventh position on our list, is it OK to write “\(e− 2\)” there or should we write “\(0.7182818284590452354. . .\)”? Clearly, it would be simpler to write “\(e − 2\)” but it isn’t necessarily possible to do something of that kind for every real number – on the other hand, writing down the decimal expansion is a problem too; in a certain sense, “most” real numbers in \((0, 1)\) have infinitely long decimal expansions. There is also another problem with decimal expansions; they aren’t unique. For example, there is really no difference between the finite expansion \(0.5\) and the infinitely long expansion \(0.4\overline{9}\).
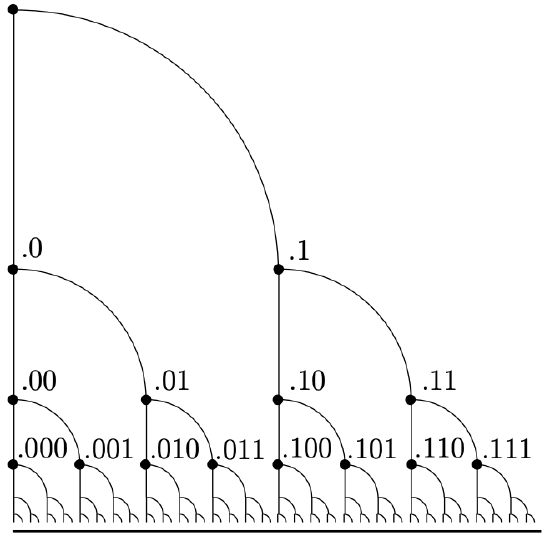
Rather than writing something like “\(e−2\)” or “\(0.7182818284590452354. . .\)”, we are going to in fact write “\(.1011011111100001010100010110001010001010 . . .\)” In other words, we are going to write the base-\(2\) expansions of the real numbers in our list. Now, the issue of non-uniqueness is still there in binary, and in fact if we were to stay in base-\(10\) it would be possible to plug a certain gap in our argument – but the binary version of this argument has some especially nice features. Every binary (or for that matter decimal) expansion corresponds to a unique real number, but it doesn’t work out so well the other way around — there are sometimes two different binary expansions that correspond to the same real number. There is a lovely fact that we are not going to prove (you may get to see this result proved in a course in Real Analysis) that points up the problem. Whenever two different binary expansions represent the same real number, one of them is a terminating expansion (it ends in infinitely many \(0\)’s) and the other is an infinite expansion (it ends in infinitely many \(1\)’s). We won’t prove this fact, but the gist of the argument is a proof by contradiction — you may be able to get the point by studying Figure \(8.3.1\). (Try to see how it would be possible to find a number in between two binary expansions that didn’t end in all-zeros and all-ones.)
So, instead of showing that the set of reals in \((0, 1)\) can’t be put in one-toone correspondence with \(\mathbb{N}\), what we’re really going to do is show that their binary expansions can’t be put in one-to-one correspondence with \(\mathbb{N}\). Since there are an infinite number of reals that have two different binary expansions this doesn’t really do the job as advertised at the beginning of this section. (Perhaps you are getting used to our wily ways by now — yes, this does mean that we’re going to ask you to do the real proof in the exercises.) The set of binary numerals, \(\{0, 1\}\), is an instance of a mathematical structure known as a field; basically, that means that it’s possible to add, subtract, multiply and divide (but not divide by \(0\)) with them. We are only mentioning this fact so
that you’ll understand why the set \(\{0, 1\}\) is often referred to as \(F_2\). We’re only mentioning that fact so that you’ll understand why we call the set of all possible binary expansion \(\mathbb{F}^∞_2\). Finally, we’re only mentioning that fact so that we’ll have a succinct way of expressing this set. Now we can write “\(\mathbb{F}^∞_2\)" rather than “the set of all possible infinitely-long binary sequences.”
Suppose we had a listing of all the elements of \(\mathbb{F}^∞_2\). We would have an infinite list of things, each of which is itself an infinite list of \(0\)’s and \(1\)’s.
So what? We need to proceed from here to find a contradiction.
This argument that we’ve been edging towards is known as Cantor’s diagonalization argument. The reason for this name is that our listing of binary representations looks like an enormous table of binary digits and the contradiction is deduced by looking at the diagonal of this infinite-by-infinite table. The diagonal is itself an infinitely long binary string — in other words, the diagonal can be thought of as a binary expansion itself. If we take the complement of the diagonal, (switch every \(0\) to a \(1\) and vice versa) we will also have a thing that can be regarded as a binary expansion and this binary expansion can’t be one of the ones on the list! This bit-flipped version of the diagonal is different from the first binary expansion in the first position, it is different from the second binary expansion in the second position, it is different from the third binary expansion in the third position, and so on. The very presumption that we could list all of the elements of \(\mathbb{F}^∞_2\) allows us to construct an element of \(\mathbb{F}^∞_2\) that could not be on the list!
This argument has been generalized many times, so this is the first in a class of things known as diagonal arguments. Diagonal arguments have been used to settle several important mathematical questions. There is a valid diagonal argument that even does what we’d originally set out to do: prove that \(\mathbb{N}\) and \(\mathbb{R}\) are not equinumerous. Strangely, the argument can’t be made to work in binary, and since you’re going to be asked to write it up in the exercises, we want to point out one of the potential pitfalls. If we were to use a diagonal argument to show that \((0, 1)\) isn’t countable, we would start by assuming that every element of \((0, 1)\) was written down in a list. For most real numbers in \((0, 1)\) we could write out their binary representation uniquely, but for some we would have to make a choice: should we write down the representation that terminates, or the one that ends in infinitely-many \(1\)’s? Suppose we choose to use the terminating representations, then none of the infinite binary strings that end with all \(1\)’s will be on the list. It’s possible that the thing we get when we complement the diagonal is one of these (unlisted) binary strings so we don’t necessarily have a contradiction. If we make the other choice – use the infinite binary representation when we have a choice – there is a similar problem. You may think that our use of binary representations for real numbers was foolish in light of the failure of the argument to “go through” in binary. Especially since, as we’ve alluded to, it can be made to work in decimal. The reason for our apparent stubbornness is that these infinite binary strings do something else that’s very nice. An infinitely long binary sequence can be thought of as the indicator function of a subset of \(\text{N}\). For example, \(.001101010001\) is the indicator of \(\{2, 3, 5, 7, 11\}\).
Complete the table.
| binary expansion | subset of \(\mathbb{N}\) |
| \(.1\) | \(\{0\}\) |
| \(.0111\) | |
| \(\{2, 4, 6\}\) | |
| \(.\overline{01}\) | |
| \(\{3k + 1 | k ∈ \mathbb{N}\}\) |
The set, \(\mathbb{F}^∞_2\), we’ve been working with is in one-to-one correspondence with the power set of the natural numbers, \(\mathcal{P}(N)\). When viewed in this light, the proof we did above showed that the power set of \(\mathbb{N}\) has an infinite cardinality strictly greater than that of \(\mathbb{N}\) itself. In other words, \(\mathcal{P}(N)\) is uncountable.
What Cantor’s theorem says is that this always works. If \(A\) is any set, and \(\mathcal{P}(A)\) is its power set then \(|A| < |\mathcal{P}(A)|\). In a way, this more general theorem is easier to prove than the specific case we just handled.
For all sets \(A\), \(A\) is not equivalent to \(\mathcal{P}(A)\).
- Proof
-
Suppose that there is a set \(A\) that can be placed in one-toone correspondence with its power set. Then there is a bijective function \(f : A \implies \mathcal{P}(A)\). We will deduce a contradiction by constructing a subset of \(A\) (i.e. a member of \(\mathcal{P}(A)\)) that cannot be in the range of \(f\).
Let \(S = \{x ∈ A | x \notin f(x)\}\).
If \(S is in the range of \(f\), there is a preimage \(y\) such that \(S = f(y)\). But, if such a \(y\) exists then the membership question, \(y ∈ S\), must either be true or false. If \(y ∈ S\), then because \(S = f(y)\), and \(S\) consists of those elements that are not in their images, it follows that \(y \notin S\). On the other hand, if \(y \notin S\) then \(y \notin f(y)\) so (by the definition of \(S\)) it follows that \(y ∈ S\). Either possibility leads to the other, which is a contradiction.
Q.E.D.
Cantor’s theorem guarantees that there is an infinite hierarchy of infinite cardinal numbers. Let’s put it another way. People have sought a construction that, given an infinite set, could be used to create a strictly larger set. For instance, the Cartesian product works like this if our sets are finite — \(A × A\) is strictly bigger than \(A\) when \(A\) is a finite set. But, as we’ve already seen, this is not necessarily so if \(A\) is infinite (remember the “snake” argument that \(\mathbb{N}\) and \(\mathbb{N}×\mathbb{N}\) are equivalent). The real import of Cantor’s theorem is that taking the power set of a set does create a set of larger cardinality. So we get an infinite tower of infinite cardinalities, starting with \(ℵ_0 = |\mathbb{N}|\), by successively taking power sets.
\[ℵ_0 = |\mathbb{N}| < |\mathcal{P}(\mathbb{N})| < |\mathcal{P}(\mathcal{P}(\mathbb{N}))| < |\mathcal{P}(\mathcal{P}(\mathcal{P}(\mathbb{N})))| < . . .\]
Exercises:
Determine a substitution rule – a consistent way of replacing one digit with another along the diagonal so that a diagonalization proof showing that the interval \((0, 1)\) is uncountable will work in decimal. Write up the proof.
Can a diagonalization proof showing that the interval \((0, 1)\) is uncountable be made workable in base-\(3\) (ternary) notation?
In the proof of Cantor’s theorem we construct a set \(S\) that cannot be in the image of a presumed bijection from \(A\) to \(\mathcal{P}(A)\). Suppose \(A = \{1, 2, 3\}\) and \(f\) determines the following correspondences: \(1 \iff ∅\), \(2 \iff \{1, 3\}\) and \(3 \iff \{1, 2, 3\}\). What is \(S\)?
An argument very similar to the one embodied in the proof of Cantor’s theorem is found in the Barber’s paradox. This paradox was originally introduced in the popular press in order to give laypeople an understanding of Cantor’s theorem and Russell’s paradox. It sounds somewhat sexist to modern ears. (For example, it is presumed without comment that the Barber is male.) In a small town, there is a Barber who shaves those men (and only those men) who do not shave themselves. Who shaves the Barber? Explain the similarity to the proof of Cantor’s theorem.
Cantor’s theorem, applied to the set of all sets leads to an interesting paradox. The power set of the set of all sets is a collection of sets, so it must be contained in the set of all sets. Discuss the paradox and determine a way of resolving it
Verify that the final deduction in the proof of Cantor’s theorem, “\((y ∈ S \implies y \notin S) ∧ (y \notin S \implies y ∈ S)\),” is truly a contradiction.


