8.2: Examples of Set Equivalence
- Page ID
- 19410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There is an ancient conundrum about what happens when an irresistible force meets an immovable object. In a similar spirit, there are sometimes heated debates among young children concerning which super-hero will win a fight. Can Wolverine take Batman? What about the Incredible Hulk versus the Thing? Certainly, Superman is at the top of the heap in this ordering. Or is he? Would the man of steel even engage in a fight with a female super-hero, say Wonder Woman? (Remember the \(1950\)’s sensibilities of Clark Kent’s alter ego.)
To many people the current topic will seem about as sensible as the schoolyard discussions just alluded to. We are concerned with knowing whether one infinite set is bigger than another, or are they the same size. There are generally three reasons that people disdain to consider such questions. The first is that, like super-heros, infinite sets are just products of the imagination. The second is that there can be no difference because “infinite is infinite” – once you get to the size we call infinity, you can’t add something to that to get to a bigger infinity. The third is that the answers to questions like this are not going to earn me big piles of money so “who cares?”
Point one is actually pretty valid. Physicists have determined that we appear to inhabit a universe of finite scope, containing a finite number of subatomic particles, so in reality there can be no infinite sets. Nevertheless, the axioms we use to study many fields in mathematics guarantee that the objects of consideration are indeed infinite in number. Infinity appears as a concept even when we know it can’t appear in actuality. Point two, the “there’s only one size of infinity” argument is wrong. We’ll see an informal argument showing that there are at least two sizes of infinity, and a more formal theorem that shows there is actually an infinite hierarchy of infinities in Section 8.3.
Point three, “who cares?” is in some sense the toughest of all to deal with. Hopefully, you’ll enjoy the clever arguments to come for their own intrinsic beauty. But, if you can figure a way to make big piles of money using this stuff that would be nice too.
Let’s get started.
Which set is bigger – the natural numbers, \(\mathbb{N}\) or the set, \(\mathbb{E}^{\text{noneg}}\), of non-negative even numbers? Both are clearly infinite, so the “infinity is infinity” camp might be lead to the correct conclusion through invalid reasoning. On the other hand, the even numbers are contained in the natural numbers so there’s a pretty compelling case for saying the evens are somehow smaller than the naturals. The mathematically rigorous way to show that these sets have the same cardinality is by displaying a one-to-one correspondence. Given an even number, how can we produce a natural to pair it with? And, given a natural how can we produce an even number to pair with it? The map \(f : \mathbb{N} \implies \mathbb{E}^{\text{noneg}}\) defined by \(f(x) = 2x\) is clearly a function, and just about as clearly, injective1. Is the map \(f\) also a surjection? In other words, is every non-negative even number the image of some natural under \(f\)? Given some non-negative even number \(e\) we need to be able to come up with an \(x\) such that \(f(x) = e\). Well, since \(e\) is an even number, by the definition of “even” we know that there is an integer \(k\) such that \(e = 2k\) and since \(e\) is either zero or positive it follows that \(k\) must also be either \(0\) or positive. It turns out that \(k\) is actually the \(x\) we are searching for. Put more succinctly, every non-negative even number \(2k\) has a preimage, \(k\), under the map \(f\). So \(f\) maps \(\mathbb{N}\) surjectively onto \(\mathbb{E}^{\text{noneg}}\). Now the sets we’ve just considered,
\(\mathbb{N} = \{0, 1, 2, 3, 4, 5, 6, . . .\}\)
and
\(\mathbb{E}^{\text{noneg}} = \{0, 2, 4, 6, 8, 10, 12, . . .\}\)
both have the feature that they can be listed – at least in principle. There is a first element, followed by a second element, followed by a third element, et cetera, in each set. The next set we’ll look at, \(\mathbb{Z}\), can’t be listed so easily. To list the integers we need to let the dot-dot-dots go both forward (towards positive infinity) and backwards (towards negative infinity),
\(\mathbb{Z} = \{. . . , −3, −2, −1, 0, 1, 2, 3, . . .\}.\)
To show that the integers are actually equinumerous with the natural numbers (which is what we’re about to do – and by the way, isn’t that pretty remarkable?) we need, essentially, to figure out a way to list the integers in a singly infinite list. Using the symbol ± we can arrange for a singly infinite listing, and if you think about what the symbol ± means you’ll probably come up with
\(\mathbb{Z} = \{0, 1, −1, 2, −2, 3, −3, . . .\}.\)
This singly infinite listing of the integers does the job we’re after in a sense – it displays a one-to-one correspondence with \(\mathbb{N}\). In fact any singly infinite listing can be thought of as displaying a one-to-one correspondence with \(\mathbb{N}\) – the first entry (or should we say zeroth entry?) in the list is corresponded with \(0\), the second entry is corresponded with \(1\), and so on.
\[\begin{array} 00\;\;\; &1\;\;\; &2\;\;\; &3\;\;\; &4\;\;\; &5\;\;\; &6\;\;\; &7\;\;\; &. . .\\ \updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \\ 0 \;\;\;&1\;\;\; &−1 \;\;\;&2 \;\;\;&−2\;\;\; &3\;\;\; &−3\;\;\; &4\;\;\; &. . . \end{array} \]
To make all of this precise we need to be able to explicitly give the oneto-one correspondence. It isn’t enough to have a picture of it – we need a formula. Notice that the negative integers are all paired with even naturals and the positive integers are all paired with odd naturals. This observation leads us to a piecewise definition for a function that gives the bijection we seek
\[ f(x)=\left\{ \begin{array}{ll} −\dfrac{x}{2} \;\;\;\;\;\;\;\text{ if } x \text{ is even}\\ \dfrac{(x + 1)}{2}\;\; \text{ if } x \text{ is odd} \end{array} \right. \]
By the way, notice that since \(0\) is even it falls into the first case, and fortunately that formula gives the “right” value.
The inverse function, \(f^{−1}\), must also be defined piecewise, but based on whether the input is positive or negative. Define the inverse function.
The examples we’ve done so far have shown that the integers, the natural numbers and the even naturals all have the same cardinality. This is the first infinite cardinal number, known as \(ℵ_0\). In a certain sense we could view both of the equivalences we’ve shown as demonstrating that \(2 ·∞ = ∞\). Our next example will lend credence to the rule: \(∞ · ∞ = ∞\). The Cartesian product of two finite sets (the set of all ordered pairs with entries from the sets in question) has cardinality equal to the product of the cardinalities of the sets. What do you suppose will happen if we let the sets be infinite? For instance, what is the cardinality of \(\mathbb{N} × \mathbb{N}\)? Consider this: the subset of ordered pairs that start with a \(0\) can be thought of as a copy of \(\mathbb{N}\) sitting inside this Cartesian product. In fact, the subset of ordered pairs starting with any particular number gives another copy of \(\mathbb{N}\) inside \(\mathbb{N} × \mathbb{N}\). There are infinitely many copies of \(\mathbb{N}\) sitting inside of \(\mathbb{N} × \mathbb{N}!\) This just really ought to get us to a larger cardinality. The surprising result that it doesn’t involves an idea sometimes known as “Cantor’s Snake” – a trick that allows us to list the elements of \(\mathbb{N} × \mathbb{N}\) in a singly infinite list2. You can visualize the set \(\mathbb{N} × \mathbb{N}\) as the points having integer coordinates in the first quadrant (together with the origin and the positive \(x\) and \(y\) axes). This set of points and the path through them known as Cantor’s snake is shown in Figure \(8.2.1\).
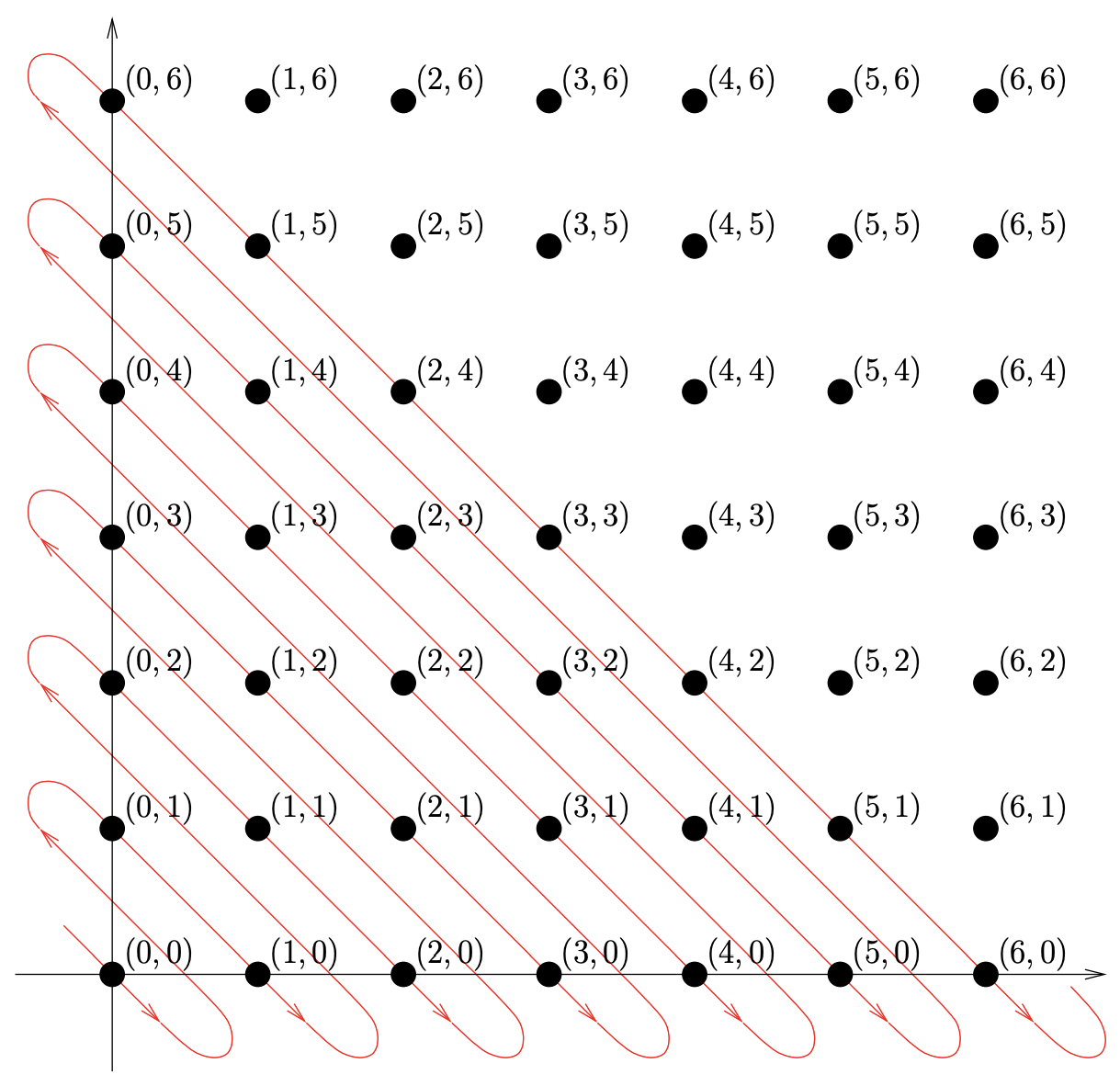
The diagram in Figure \(8.2.1\) gives a visual form of the one-to-one correspondence we seek. In tabular form, we would have something like the following.
\[\begin{array} 00\;\;\; &1\;\;\; &2\;\;\; &3\;\;\; &4\;\;\; &5\;\;\; &6\;\;\; &7\;\;\;&8\;\;\; &. . .\\ \updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow\;\;\;&\updownarrow \;\;\;&\updownarrow \\ (0,0) \;\;\;&(0,1)\;\;\; &(1,0) \;\;\;&(0,2) \;\;\;&(1,1)\;\;\; &(2,0)\;\;\; &(0,3)\;\;\; &(1,2)\;\;\;&(2,1)\;\;\; &. . . \end{array} \]
We need to produce a formula. In truth, we should really produce two formulas. One that takes an ordered pair \((x, y)\) and produces a number \(n\). Another that takes a number n and produces an ordered pair \((x, y)\) The number \(n\) tells us where the pair (\(x, y)\) lies in our infinite listing. There is a problem though: the second formula (that gives the map from \(\mathbb{N}\) to \(\mathbb{N} × \mathbb{N}\)) is really hard to write down – it’s easier to describe the map algorithmically. A simple observation will help us to deduce the various formulas. The ordered pairs along the y-axis (those of the form (\(0\), something)) correspond to triangular numbers. In fact the pair \((0, n)\) will correspond to the \(n\)-th triangular number, \(T(n) = \dfrac{(n^2 + n)}{2}\). The ordered pairs along the descending slanted line starting from \((0, n)\) all have the feature that the sum of their coordinates is \(n\) (because as the \(x\)-coordinate is increasing, the \(y\)-coordinate is decreasing). So, given an ordered pair \((x, y)\), the number corresponding to the position at the upper end of the slanted line it is on (which will have coordinates \((0, x+y))\) will be \(T(x+y)\), and the pair \((x, y)\) occurs in the listing exactly \(x\) positions after \((0, x + y)\). Thus, the function \(f : \mathbb{N} × \mathbb{N} \implies \mathbb{N}\) is given by
\[f(x, y) = x + T(x + y) = x + \dfrac{(x + y)^2 + (x + y)}{2} .\]
To go the other direction – that is, to take a position in the listing and derive an ordered pair – we need to figure out where a given number lies relative to the triangular numbers. For instance, try to figure out what \((x, y)\) pair position number \(13\) will correspond with. Well, the next smaller triangular number is \(10\) which is \(T(4)\), so \(13\) will be the number of an ordered pair along the descending line whose \(y\)-intercept is \(4\). In fact, \(13\) will be paired with an ordered pair having a \(3\) in the \(x\)-coordinate (since \(13\) is \(3\) larger than \(10\)) so it follows that \(f^{−1} (13) = (3, 1)\).
Of course we need to generalize this procedure. One of the hardest parts of finding that generalization is finding the number \(4\) in the above example (when we just happen to notice that \(T(4) = 10\)). What we’re really doing there is inverting the function \(T(n)\). Finding an inverse for \(T(n) = \dfrac{(n^2+n)}{2}\) was the essence of one of the exercises in Section 6.6. The parabola \(y = \dfrac{(x^2 + x)}{2}\) has roots at \(0\) and \(−1\) and is scaled by a factor of \(\dfrac{1}{2}\) relative to the “standard” parabola \(y = x^2\). Its vertex is at (\(−\dfrac{1}{2}, −\dfrac{1}{8})\). The graph of the inverse relation is, of course, obtained by reflecting through the line \(y = x\) and by considering scaling and horizontal/vertical translations we can deduce a formula for a function that gives a right inverse for \(T\),
\[T^{−1} (x) = \sqrt{2x + \dfrac{1}{4}} − \dfrac{1}{2}.\]
So, given \(n\), a position in the listing, we calculate \(A = \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor\). The \(x\)-coordinate of our ordered pair is \(n−T(A)\) and the \(y\)-coordinate is \(A−x\). It is not pretty, but the above discussion can be translated into a formula for \(f^{−1}\).
\[f^{−1} (n) = \left( n − \dfrac{\left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor^2 + \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor}{2} , \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor − n + \dfrac{\left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor^2 + \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor}{2} \right).\]
When restricted to the appropriate sets (\(f\)’s domain is restricted to \(\mathbb{N}×\mathbb{N}\) and \(f^{−1}\)’s domain is restricted to \(\mathbb{N}\)), these functions are two-sided inverses for one another. That fact is sufficient to prove that \(f\) is bijective. So far we have shown that the sets \(\mathbb{E}^{\text{noneg}}, \(\mathbb{N}\), \(\mathbb{Z}\) and \(\mathbb{N} × \mathbb{N}\) all have the same cardinality — \(ℵ_0\). We plan to provide an argument that there actually are other infinite cardinals in the next section. Before leaving the present topic (examples of set equivalence) we’d like to present another nice technique for deriving the bijective correspondences we use to show that sets are equivalent – geometric constructions. Consider the set of points on the line segment \([0, 1]\). Now consider the set of points on the line segment \([0, 2]\). This second line segment, being twice as long as the first, must have a lot more points on it. Right?
Well, perhaps you’re getting used to this sort of thing. . . The interval \([0, 1]\) is a subset of the interval \([0, 2]\), but since both represent infinite sets of points it’s possible they actually have the same cardinality. We can prove that this is so using a geometric technique. We position the line segments appropriately and then use projection from a carefully chosen point to develop a bijection. Imagine both intervals as lying on the \(x\)-axis in the \(x\)-\(y\) plane. Shift the smaller interval up one unit so that it lies on the line \(y = 1\). Now, use projection from the point \((0, 2)\), to visualize the correspondence see Figure \(8.2.2\).
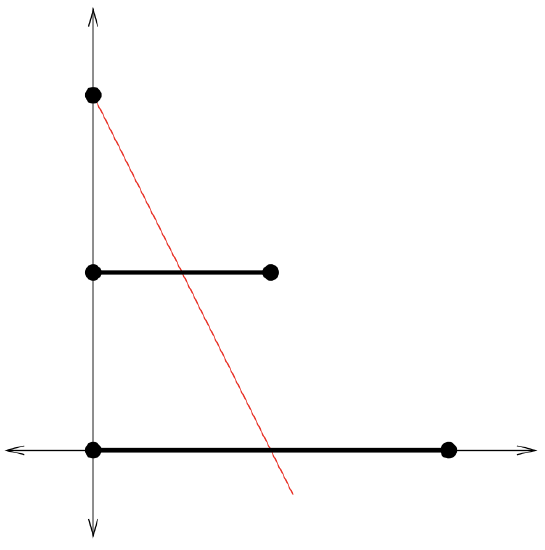
By considering appropriate projections we can prove that any two arbitrary intervals (say \([a, b]\) and \([c, d]\)) have the same cardinalities! It also isn’t all that hard to derive a formula for a bijective function between two intervals.
\[f(x) = c + \dfrac{(x − a)(d − c)}{(b − a)}\]
There are other geometric constructions which we can use to show that there are the same number of points in a variety of entities. For example, consider the upper half of the unit circle (Remember the unit circle from Trig? All points \((x, y)\) satisfying \(x^2 + y^2 = 1\).) This is a semi-circle having a radius of \(1\), so the arclength of said semi-circle is \(π\). It isn’t hard to imagine that this semi-circular arc contains the same number of points as an interval of length \(π\), and we’ve already argued that all intervals contain the same number of points. . . But, a nice example of geometric projection — vertical projection (a.k.a. \(π_1\)) — can be used to show that (for example) the interval \((−1, 1)\) and the portion of the unit circle lying in the upper half-plane are equinumerous.
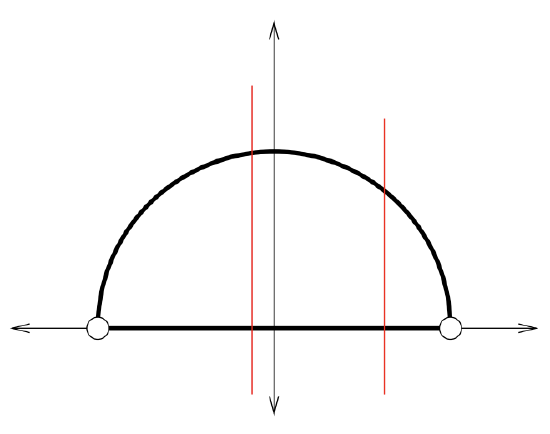
Once the bijection is understood geometrically it is fairly simple to provide formulas. To go from the semi-circle to the interval, we just forget about the \(y\)-coordinate:
\[f(x, y) = x.\]
To go in the other direction we need to recompute the missing \(y\)-value:
\[f^{−1} (x) = (x, \sqrt{1 − x^2}).\]
Now we’re ready to put some of these ideas together in order to prove something really quite remarkable. It may be okay to say that line segments of different lengths are equinumerous – although ones intuition still balks at the idea that a line a mile long only has the same number of points on it as a line an inch long (or, if you prefer, make that a centimeter versus a kilometer). Would you believe that the entire line – that is the infinitely extended line – has no more points on it than a tiny little segment? You should be ready to prove this one yourself.
Find a point such that projection from that point determines a one-to-one correspondence between the portion of the unit circle in the upper half plane and the line \(y = 1\).
In the exercises from Section 8.1 you were supposed to show that set equivalence is an equivalence relation. Part of that proof should have been showing that the relation is transitive, and that really just comes down to showing that the composition of two bijections is itself a bijection. If you didn’t make it through that exercise give it another try now, but whether or not you can finish that proof it should be evident what that transitivity means to us in the current situation. Any pair of line segments are the same size – a line segment (i.e. an interval) and a semi-circle are the same size – the semi-circle and an infinite line are the same size – transitivity tells us that an infinitely extended line has the same number of points as (for example) the interval \((0, 1)\).
Exercises:
Prove that positive numbers of the form \(3k + 1\) are equinumerous with positive numbers of the form \(4k + 2\).
Prove that \(f(x) = c + \dfrac{(x − a)(d − c)}{(b − a)}\) provides a bijection from the interval \([a, b]\) to the interval \([c, d]\).
Prove that any two circles are equinumerous (as sets of points).
Determine a formula for the bijection from \((−1, 1)\) to the line \(y = 1\) determined by vertical projection onto the upper half of the unit circle, followed by projection from the point \((0, 0)\).
It is possible to generalize the argument that shows a line segment is equivalent to a line to higher dimensions. In two dimensions we would show that the unit disk (the interior of the unit circle) is equinumerous with the entire plane \(\mathbb{R} × \mathbb{R}\). In three dimensions we would show that the unit ball (the interior of the unit sphere) is equinumerous with the entire space \(\mathbb{R}^3 = \mathbb{R} × \mathbb{R} × \mathbb{R}\). Here we would like you to prove the two-dimensional case.
Gnomonic projection is a style of map rendering in which a portion of a sphere is projected onto a plane that is tangent to the sphere. The sphere’s center is used as the point to project from. Combine vertical projection from the unit disk in the \(x\)–\(y\) plane to the upper half of the unit sphere \(x^2 + y^2 + z^2 = 1\), with gnomonic projection from the unit sphere to the plane \(z = 1\), to deduce a bijection between the unit disk and the (infinite) plane.


