1.6: Sequences
- Page ID
- 101009
In calculus we think of a sequence as a (possibly infinite) list of objects. We shall expand on that idea somewhat, and express it in the language of functions.
A finite sequence is a function \(f\) with domain \(\ulcorner N\urcorner\), where \(N \in \mathbb{N}\). We often identify the sequence with the ordered finite set \(\left\langle a_{n} \mid n<N\right\rangle\), where \(a_{n}=f(n)\), for \(0 \leq n<N\).
This interpretation of a sequence as a type of function is easily extended to infinite sequences.
An infinite sequence is a function \(f\) with domain \(\mathbb{N}\). We often identify the sequence with the ordered infinite set \(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\), where \(a_{n}=f(n)\), for \(n \in \mathbb{N}\).
REMARK. Interval in \(\mathbb{Z}\) Actually, the word sequence is normally used to mean any function whose domain is an interval in \(\mathbb{Z}\), where an interval in \(\mathbb{Z}\) is the intersection of some real interval with \(\mathbb{Z}\). For convenience in this book, we usually assume that the first element of any sequence is indexed by 0 or 1 .
The sequence \(\langle 0,1,4,9, \ldots\rangle\) is given by the function \(f(n)=n^{2} .\)
The sequence \(\langle 1,-1,2,-2,3,-3, \ldots\rangle\) is given by the function \[f(n)= \begin{cases}\frac{n}{2}+1, & n \text { even } \\ -\frac{n+1}{2}, & n \text { odd. }\end{cases}\] Sequences can take values in any set (the codomain of the function \(f\) that defines the sequence). We talk of a real sequence if the values are real numbers, an integer sequence if they are all integers, etc. It will turn out later that sequences with values in the two element set \(\{0,1\}\) occur quite frequently, so we have a special name for them: we call them binary sequences.
A finite binary sequence is a function, \(f:\ulcorner N\urcorner \rightarrow\ulcorner 2\urcorner\), for some \(N \in \mathbb{N}\). An infinite binary sequence is a function, \(f: \mathbb{N} \rightarrow\ulcorner 2\urcorner\).
We often use the expression \(\left\langle a_{n}\right\rangle\) for the sequence \(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\).
Functions are also used to "index" sets in order to build more complicated sets with generalized set operations. We discussed the union (or intersection) of more than two sets. You might ask whether it is possible to form unions or intersections of a large (infinite) collection of sets. There are two concerns that should be addressed in answering this question. We must be sure that the definition of the union of infinitely many sets is precise; that is, it uniquely characterizes an object in the mathematical universe. We also need notation for managing this idea - how do we specify the sets over which we are taking the union?
For \(n \in \mathbb{N}^{+}\), let \(X_{n}\) be a set. Then \[\bigcup_{n=1}^{\infty} X_{n}=\left\{x \mid \text { for some } n \in \mathbb{N}^{+}, x \in X_{n}\right\} \text {. }\] The set \(\mathbb{N}^{+}\)is called the index set for the union.
This may be written in a few different ways.
NOTATION. \(\bigcup_{n \in \mathbb{N}^{+}} X_{n}\) The following three expressions are all equal:
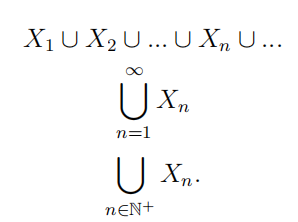
We can use index sets other than \(\mathbb{N}^{+}\).
Let \(A\) be a set, and for \(\alpha \in A\), let \(X_{\alpha}\) be a set. The set \[\mathcal{F}=\left\{X_{\alpha} \mid \alpha \in A\right\}\] is called a family of sets indexed by \(A\). Then \[\bigcup_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for some } \alpha \in A\right\} \text {. }\] The notation \(\bigcup_{\alpha \in A} X_{\alpha}\) is read "the union over alpha in A of the sets X sub alpha". So \[x \in \bigcup_{\alpha \in A} X_{\alpha} \text { if } x \in X_{\alpha} \text { for some } \alpha \in A \text {. }\] General intersections over a family of sets are defined analogously : \[\bigcap_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for all } \alpha \in A\right\} .\] ExAMPLE 1.43. Let \(X_{n}=\{n+1, n+2, \ldots, 2 n\}\) for each \(n \in \mathbb{N}^{+}\). Then \[\begin{aligned} &\bigcup_{n=1}^{\infty} X_{n}=\{k \in \mathbb{N} \mid k \geq 2\} \\ &\bigcap_{n=1}^{\infty} X_{n}=\emptyset . \end{aligned}\] Example 1.44. For each positive real number \(t\), let \(Y_{t}=[11 / t, t]\). Then \[\begin{aligned} \bigcup_{t \in(\sqrt{11}, \infty)} Y_{t} &=\mathbb{R}^{+} \\ \bigcap_{t \in[\sqrt{11}, \infty)} Y_{t} &=\{\sqrt{11}\} . \end{aligned}\] ExAMPLE 1.45. Let \(f: X \rightarrow Y, A \subseteq X\) and \(B \subseteq Y\). Then \[\bigcup_{a \in A}\{f(a)\}=f[A] .\] and \[\bigcup_{b \in B} f^{-1}(b)=f^{-1}[B] .\]