9.1: Cubics
- Page ID
- 99108
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)How does one find the roots of a cubic polynomial? The Babylonians knew the quadratic formula in the second millennium BC, but a formula for the cubic was only found in the \(16^{\text {th }}\) century. The history of the discovery is complicated, but most of the credit should go to Nicolo Tartaglia. The solution was published in 1545 in Girolomo Cardano’s very influential book Artis magnae sive de regulis algebraicis liber unus. Formula \(9.2\) is known today as the Tartaglia-Cardano formula. For a historical account, see e.g. [6].
Consider a cubic polynomial in \(\mathbb{R}[x]\) \[p(x)=a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0} .\] If we want to find the roots, there is no loss of generality in assuming that \(a_{3}=1\), since the zeroes of \(p\) are the same as the zeroes of \(\frac{1}{a_{3}} p\).
The second simplification is that we can assume \(a_{2}=0\). Indeed, make the change of variable \[x=y-\beta,\] for some \(\beta\) to be chosen later. Then \[\begin{aligned} p(x) &=x^{3}+a_{2} x^{2}+a_{1} x+a_{0} \\ &=(y-\beta)^{3}+a_{2}(y-\beta)^{2}+a_{1}(y-\beta)+a_{0} \\ &=y^{3}+\left[a_{2}-3 \beta\right] y^{2}+\left[a_{1}-2 a_{2} \beta+3 \beta^{2}\right] y+\left[a_{0}-a_{1} \beta+a_{2} \beta^{2}-\beta^{3}\right] \\ &=: \quad q(y) . \end{aligned}\] Choose \(\beta=a_{2} / 3\). Then the coefficient of \(y^{2}\) in \(q(y)\) vanishes. Suppose you can find the roots of \(q\), call them \(\alpha_{1}, \alpha_{2}, \alpha_{3}\). Then the roots of the original polynomial \(p\) are \(\alpha_{1}-\beta, \alpha_{2}-\beta, \alpha_{3}-\beta\).
Therefore it is sufficient to find a formula for the roots of a cubic in which the quadratic term vanishes. This is called a reduced cubic. As there are now only two coefficients left, we shall drop the subscripts and write our reduced cubic as \[q(x)=x^{3}+a x+b .\] The key idea is to make another, more ingenious, substitution. Let us introduce a new variable \(w\), related to \(x\) by \[x=w+\frac{c}{w},\] where \(c\) is a constant we shall choose later. Then \[\begin{aligned} q(x) &=\left(w+\frac{c}{w}\right)^{3}+a\left(w+\frac{c}{w}\right)+b \\ &=w^{3}+[3 c+a] w+\left[3 c^{2}+a c\right] \frac{1}{w}+c^{3} \frac{1}{w^{3}}+b . \end{aligned}\] Choose \[c=-\frac{a}{3},\] so both the coefficient of \(w\) and \(1 / w\) in (9.4) vanish. Then finding \(x\) so that \(q(x)=0\) is the same as finding \(w\) so that \[\begin{aligned} w^{3}+\frac{c^{3}}{w^{3}}+b &=0 \\ \Longleftrightarrow w^{6}+b w^{3}+c^{3} &=0 . \end{aligned}\] Equation (9.5) is of degree 6, which seems worse than the original cubic; but so many terms vanish that it is actually a quadratic equation in \(w^{3}\). Therefore it can solved by the quadratic formula: \[w^{3}=\frac{-b \pm \sqrt{b^{2}-4 c^{3}}}{2} .\] Knowing \(w\), we can recover \(x\) by \[x=w+\frac{c}{w}=w-\frac{a}{3 w} .\] So we arrive at the Tartaglia-Cardano formula for the roots of the reduced cubic (9.2): \[x=\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}-\frac{a}{3\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}} .\] How does the formula work in practice?
EXAMPLE 9.8. Let \(p(x)=x^{3}-3 x+2\). Then \(c=1\), and (9.6) says \(w^{3}=-1\). Therefore \(w=-1\), and so \(x=-2\) is a root. Therefore, by Lemma \(4.13,(x+2)\) is a factor of \(p\). Factoring, we get \[x^{3}-3 x+2=(x+2)\left(x^{2}-2 x+1\right) .\] The last term factors as \((x-1)^{2}\), so we conclude that the roots are \(-2,1,1\).
In Example 9.8, the formula worked, but only gave us one of the roots. Consider the next example:
EXAMPLE 9.9. Let \[p(x)=x^{3}-3 x+1 .\] Then \(c=1\), and \[w^{3}=\frac{-1 \pm \sqrt{-3}}{2} .\] Now we have a worse problem: \(w^{3}\) involves the square root of a negative number, and even if we make sense of that, we then have to extract a cube root. Is this analagous to trying to solve the quadratic equation \[q(x):=x^{2}+x+1=0 ?\] The quadratic formula again gives the right-hand side of \((9.11)\), and we explain this by saying that in fact \(q\) has no real roots. Indeed, graphing shows that \(q\) looks like Figure 9.12.
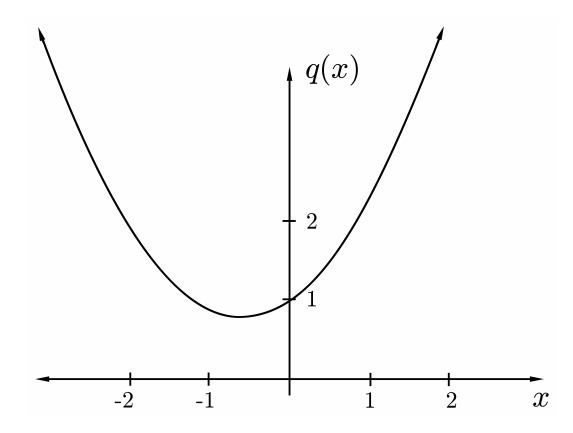
But this cannot be the case for \(p\). Indeed, \[\begin{aligned} p(-2) &=-1<0 \\ p(0) &=1>0 \\ p(1) &=-1<0 \\ p(2) &=3>0 \end{aligned}\] Therefore, by the Intermediate Value Theorem \(8.10, p\) must have a root in each of the intervals \((-2,0),(0,1)\) and \((1,2)\). As \(p\) can have at most 3 roots by Theorem \(4.10\), it must therefore have exactly three roots. A graph of \(p\) looks like Figure 9.13.
It turns out that one can find the roots of \(p\) in Example \(9.9\) by correctly interpreting the Tartaglia-Cardano formula. We shall come back to this example in Section 9.3, after we develop the necessary ideas. The big idea is to introduce the notion of a complex number.


