9.2: Complex Numbers
- Page ID
- 99109
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)DEFINITION. Complex number A complex number is an expression of the form \(a+i b\), where \(a\) and \(b\) are real numbers.
For the moment, you can think of the \(i\) in \(a+i b\) as a formal symbol, or a place-holder. Later, we shall see that it has another interpretation.
Notation. \(\mathbb{C}\) We shall let \(\mathbb{C}\) denote the set of all complex numbers: \[\mathbb{C}=\{a+i b: a, b \in \mathbb{R}\} .\] As a set, one can identify \(\mathbb{C}\) with \(\mathbb{R}^{2}\) in the obvious way. This allows us to define addition; what is not so obvious is that there is also a good definition for multiplication.
DEFINITION. Let \(a+i b\) and \(c+i d\) be complex numbers. Then their sum and product are defined by \[\begin{aligned} (a+i b)+(c+i d) &=(a+c)+i(b+d) \\ (a+i b) \times(c+i d) &=(a c-b d)+i(a d+b c) . \end{aligned}\] The formula for the sum (9.14) is just what you would get if you identified the complex number \(a+i b\) with the vector \((a, b)\) in \(\mathbb{R}^{2}\) and used vector addition. The product is more subtle. If you multiply out the left-hand side of (9.15), you get \[a c+i(a d+b c)+i^{2} b d .\] One arrives at the right-hand side of (9.15) by defining \[i^{2}=-1 \text {. }\] So \(i\) is the square root of \(-1\); that is, it is an algebraic quantity we introduce that is defined to have the property that its square is \(-1\). Obviously this precludes \(i\) from being a real number.
In essence we have continued the program of defining number systems that we began in Chapter 8. Addition and multiplication of complex numbers have been defined by algebraic operations on \(\mathbb{R} \times \mathbb{R}\). Since algebraic operations on the real numbers were defined set-theoretically, we have thereby defined algebraic operations on \(\mathbb{C}\) by set operations. Unlike the other numbers systems we have defined, we do not define a linear ordering of \(\mathbb{C}\). It is not generally useful to think of complex numbers on a number line. However it is very useful to think of complex numbers as points in the plane \(\mathbb{R}^{2}\), and to describe them in polar coordinates.
As usual, the point with Cartesian coordinates \((x, y)\) has polar coordinates \((r, \theta)\), where they are related by \[\begin{array}{cl} r=\sqrt{x^{2}+y^{2}} & \tan (\theta)=y / x \\ x=r \cos \theta & y=r \sin \theta . \end{array}\] So the complex number \(z=x+i y\) can also be written as \[z=r(\cos \theta+i \sin \theta) .\] The form (9.18) is so widely used that there is a special notation for it.
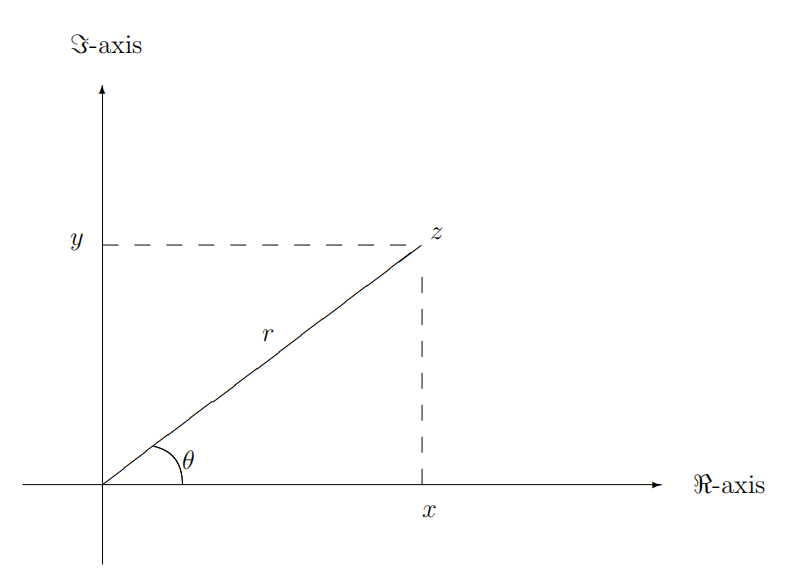
Notation. Cis \[\operatorname{Cis}(\theta):=\cos \theta+i \sin \theta .\] DEFINITION. For the complex number \(z=x+i y=r \operatorname{Cis}(\theta)\), we have the following:
\(\Re(z) x\) is called the real part of \(z\), written \(\Re(z)\);
\(\Im(z) y\) is called the imaginary part of \(z\), written \(\Im(z)\);
\(|z| r\) is called the modulus of \(z\), or absolute value of \(z\), written \(|z|\); \(\arg (z) \theta\) is called the argument of \(z\), written \(\arg (z)\).
\(\bar{z}\) The number \(x-i y\) is called the conjugate of \(z\), written \(\bar{z}\).
REMARK. There is an important point to bear in mind about the argument: it is only unique up to addition of multiples of \(2 \pi\). In other words, if \(\theta_{0}\) is an argument of the complex number \(z\), then so are all the numbers \(\left\{\theta_{0}+2 k \pi: k \in \mathbb{Z}\right\}\). Addition is easiest in Cartesian coordinates: add the real and imaginary parts. Multiplication is easiest in polar coordinates: multiply the moduli and add the arguments.
Proposition 9.19. Let \(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) and \(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Then \[z_{1} z_{2}=r_{1} r_{2} \operatorname{Cis}\left(\theta_{1}+\theta_{2}\right) .\] ProOF. Multiplying out, we get \[\begin{aligned} z_{1} z_{2}=r_{1} r_{2}\left[\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}\right.\\ &\left.+i\left(\cos \theta_{1} \sin \theta_{2}+\cos \theta_{2} \sin \theta_{1}\right)\right] . \end{aligned}\] The result follows by the trigonometric identities for the cosine and sine of the sum of two angles.
A consequence of Proposition \(9.19\) is the following formula for raising a complex number to a power, called De Moivre’s theorem.
THEOREM 9.20. De Moivre’s Theorem Let \(z=r \operatorname{Cis}(\theta)\) be a nonzero complex number, and let \(n \in \mathbb{Z}\). Then \[z^{n}=r^{n} \operatorname{Cis}(n \theta) .\] ProOF. If \(n \geq 0\), then \((9.21)\) can be proved by induction from Proposition 9.19. For \(n\) negative, it is enough to observe that by Proposition \(9.19\) \[[r \operatorname{Cis}(\theta)]\left[r^{-1} \operatorname{Cis}(-\theta)\right]=1 \operatorname{Cis}(0)=1 .\] We can now prove that every non-zero complex number has exactly \(n\) distinct \(n^{\text {th }}\) roots.
THEOREM 9.22. Let \(z=r \operatorname{Cis}(\theta)\) be a non-zero complex number, and let \(n\) be an integer greater than 1 . Then there are exactly \(n\) complex numbers \(w\) satisfying the equation \(w^{n}=z\). They are \[\left\{r^{1 / n} \operatorname{Cis}\left(\frac{\theta}{n}+\frac{2 k \pi}{n}\right): k=0,1, \ldots, n-1\right\} .\] Proof. Suppose \(w=\rho \operatorname{Cis}(\phi)\) is an \(n^{\text {th }}\) root of \(z\). Then by De Moivre’s theorem, \(\rho^{n}=r\) and \(n \phi\) is an argument of \(z\). As \(\rho\) must be a positive real number, it is the unique positive \(n^{\text {th }}\) root of \(r\). The number \(n \phi\) can be any argument of \(z\), so we have \[n \phi=\theta+2 k \pi, \quad k \in \mathbb{Z} .\] So \(\phi\) can have the form \[\frac{\theta}{n}+\frac{2 k \pi}{n}\] for any integer \(k\). However, different \(\phi\) ’s will give rise to the same complex number \(w\) if they differ by a multiple of \(2 \pi\). So there are exactly \(n\) different \(w\) ’s that are \(n^{\text {th }}\) roots of \(z\).
EXAMPLE 9.24. What does Theorem \(9.22\) tell us are the square roots of \(-1\) ? We let \(r=1\) and \(\theta=\pi\), and we get the square roots are \(\operatorname{Cis}(\pi / 2)=i\) and \(\operatorname{Cis}(-\pi / 2)=-i\).
EXAMPLE 9.25. Find the cube roots of \(1 .\)
In the notation of Theorem \(9.22, r=1\) and \(\theta=0\). Therefore the cube roots are \[\begin{aligned} 1 &=\operatorname{Cis}(2 \pi / 3)=-\frac{1}{2}+i \frac{\sqrt{3}}{2} \\ \omega^{2} &=\operatorname{Cis}(4 \pi / 3)=-\frac{1}{2}-i \frac{\sqrt{3}}{2} . \end{aligned}\] The number \(\omega\) is called a primitive cube root of unity, because all the cube roots are obtained as \(\omega, \omega^{2}, \omega^{3}\).
DEFINITION. Primitive root of unity A primitive \(n^{\text {th }}\) root of unity is a number \(\omega\) such that \(\left\{1, \omega, \omega^{2}, \ldots, \omega^{n-1}\right\}\) constitute all the \(n^{\text {th }}\) roots of 1 .
Proposition 9.26. Let \(z\) be a complex number, and \(w_{0}\) be some \(n^{\text {th }}\) root of \(z\). Let \(\omega\) be a primitive \(n^{\text {th }}\) root of unity. Then all the \(n^{\text {th }}\) roots of \(z\) are \(\left\{w_{0}, \omega w_{0}, \omega^{2} w_{0}, \ldots, \omega^{n-1} w_{0}\right\}\).


