1.4: Add Whole Numbers (Part 2)
- Page ID
- 5767
Translate Word Phrases to Math Notation
Earlier in this section, we translated math notation into words. Now we’ll reverse the process. We’ll translate word phrases into math notation. Some of the word phrases that indicate addition are listed in Table \(\PageIndex{2}\).
| Operation | Words | Example | Expression |
|---|---|---|---|
| Addition | plus | 1 plus 2 | 1 + 2 |
| sum | the sum of 3 and 4 | 3 + 4 | |
| increased by | 5 increased by 6 | 5 + 6 | |
| more than | 8 more than 7 | 7 + 8 | |
| total of | the total of 9 and 5 | 9 + 5 | |
| added to | 6 added to 4 | 4 + 6 |
Translate and simplify: the sum of 19 and 23.
Solution
The word sum tells us to add. The words of \(19\) and \(23\) tell us the addends.
| The sum of 19 and 23 | |
| Translate. | 19 + 23 |
| Add. | 42 |
| The sum of 19 and 23 is 42. |
Translate and simplify: the sum of \(17\) and \(26\).
- Answer
-
Translate:
Translate and simplify: the sum of \(28\) and \(14\).
- Answer
-
Translate: \(28+14\); Simplify: \(42\)
Translate and simplify: \(28\) increased by \(31\).
Solution
The words increased by tell us to add. The numbers given are the addends.
| 28 increased by 31. | |
| Translate. | 28 + 31 |
| Add. | 59 |
| So 28 increased by 31 is 59. |
Translate and simplify: \(29\) increased by \(76\).
- Answer
-
Translate: \(29+76\); Simplify: \(105\)
Translate and simplify: \(37\) increased by \(69\).
- Answer
-
Translate: \(37+69\); Simplify: \(106\)
Add Whole Numbers in Applications
Now that we have practiced adding whole numbers, let’s use what we’ve learned to solve real-world problems. We’ll start by outlining a plan. First, we need to read the problem to determine what we are looking for. Then we write a word phrase that gives the information to find it. Next we translate the word phrase into math notation and then simplify. Finally, we write a sentence to answer the question.
Hao earned grades of \(87, 93, 68, 95,\) and \(89\) on the five tests of the semester. What is the total number of points he earned on the five tests?
Solution
We are asked to find the total number of points on the tests.
| Write a phrase. | the sum of points on the tests |
| Translate to math notation. | 87 + 93 + 68 + 95 + 89 |
| Then we simplify by adding | |
| Since there are several numbers, we will write them vertically. |  |
| Write a sentence to answer the question. | Hao earned a total of 432 points. |
Notice that we added points, so the sum is \(432\) points. It is important to include the appropriate units in all answers to applications problems.
Mark is training for a bicycle race. Last week he rode \(18\) miles on Monday, \(15\) miles on Wednesday, \(26\) miles on Friday, \(49\) miles on Saturday, and \(32\) miles on Sunday. What is the total number of miles he rode last week?
- Answer
-
He rode \(140\) miles.
Lincoln Middle School has three grades. The number of students in each grade is \(230, 165,\) and \(325\). What is the total number of students?
- Answer
-
The total number is \(720\) students.
Some application problems involve shapes. For example, a person might need to know the distance around a garden to put up a fence or around a picture to frame it. The perimeter is the distance around a geometric figure. The perimeter of a figure is the sum of the lengths of its sides.
Find the perimeter of the patio shown.
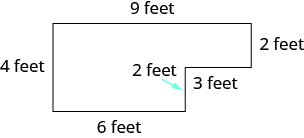
Figure \(\PageIndex{3}\)
Solution
| We are asked to find the perimeter. | |
| Write a phrase. | the sum of the sides |
| Translate to math notation. | 4 + 6 + 2 + 3 + 2 + 9 |
| Simplify by adding. | 26 |
| Write a sentence to answer the question. | |
| We added feet, so the sum is 26 feet. | The perimeter of the patio is 26 feet. |
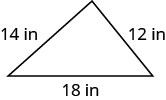
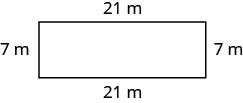
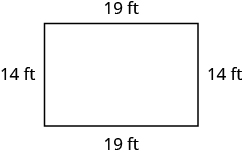
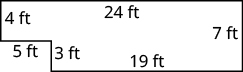
Find the perimeter of each figure. All lengths are in inches.
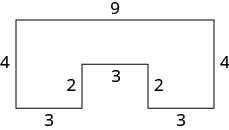
Figure \(\PageIndex{4}\)
- Answer
-
The perimeter is \(30\) inches.
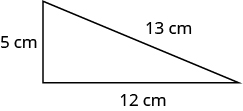
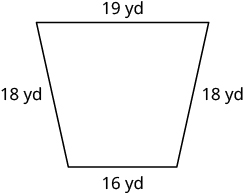
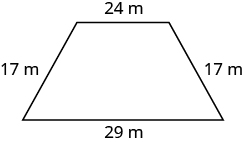
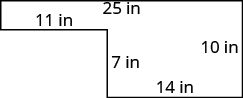
Find the perimeter of each figure. All lengths are in inches.
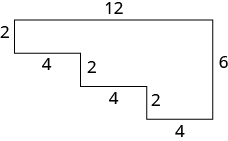
Figure \(\PageIndex{5}\)
- Answer
-
The perimeter is \(36\) inches.
Access Additional Online Resources
Key Concepts
- Addition Notation To describe addition, we can use symbols and words.
Operation Notation Expression Read as Result Addition three plus four the sum of - Identity Property of Addition
- The sum of any number \(
- Commutative Property of Addition
- Changing the order of the addends \(
- Add whole numbers.
- Write the numbers so each place value lines up vertically.
- Add the digits in each place value. Work from right to left starting with the ones place. If a sum in a place value is more than \(9\), carry to the next place value.
- Continue adding each place value from right to left, adding each place value and carrying if needed.
Glossary
- sum
-
The sum is the result of adding two or more numbers.
Practice Makes Perfect
Use Addition Notation
In the following exercises, translate the following from math expressions to words.
- 5 + 2
- 6 + 3
- 13 + 18
- 15 + 16
- 214 + 642
- 438 + 113
Model Addition of Whole Numbers
In the following exercises, model the addition
- 2 + 4
- 5 + 3
- 8 + 4
- 5 + 9
- 14 + 75
- 15 + 63
- 16 + 25
- 14 + 27
Add Whole Numbers
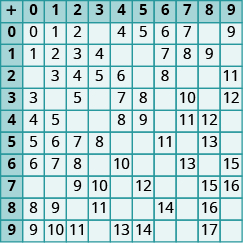
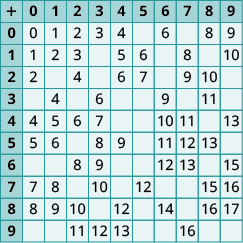
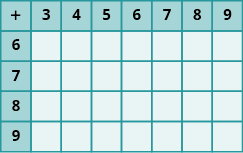
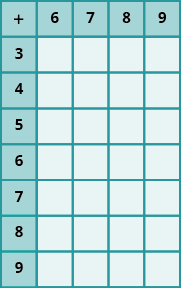
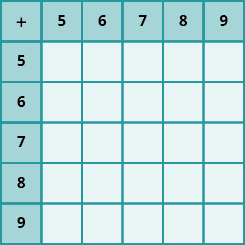
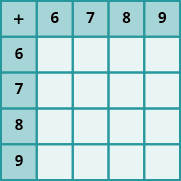
In the following exercises, fill in the missing values in each chart
In the following exercises, add.
- (a) 0 + 13 (b) 13 + 0
- (a) 0 + 5,280 (b) 5,280 + 0
- (a) 8 + 3 (b) 3 + 8
- (a) 7 + 5 (b) 5 + 7
- 45 + 33
- 37 + 22
- 71 + 28
- 43 + 53
- 26 + 59
- 38 + 17
- 64 + 78
- 82 + 39
- 168 + 325
- 247 + 149
- 584 + 277
- 175 + 648
- 832 + 199
- 775 + 369
- 6,358 + 492
- 9,184 + 578
- 3,740 + 18,593
- 6,118 + 15,990
- 485,012 + 649,848
- 368,911 + 587,289
- 24,731 + 592 + 3,868
- 28,925 + 817 + 4,593
- 8,015 + 76,946 + 16,570
- 6,291 + 54,107 + 28,635
Translate Word Phrases to Math Notation
In the following exercises, translate each phrase into math notation and then simplify
- the sum of 13 and 18
- the sum of 12 and 19
- the sum of 90 and 65
- the sum of 70 and 38
- 33 increased by 49
- 68 increased by 25
- 250 more than 599
- 115 more than 286
- the total of 628 and 77
- the total of 593 and 79
- 1,482 added to 915
- 2,719 added to 682
Add Whole Numbers in Applications
In the following exercises, solve the problem.
- Home remodeling Sophia remodeled her kitchen and bought a new range, microwave, and dishwasher. The range cost $1,100, the microwave cost $250, and the dishwasher cost $525. What was the total cost of these three appliances?
- Sports equipment Aiden bought a baseball bat, helmet, and glove. The bat cost $299, the helmet cost $35, and the glove cost $68. What was the total cost of Aiden’s sports equipment?
- Bike riding Ethan rode his bike 14 miles on Monday, 19 miles on Tuesday, 12 miles on Wednesday, 25 miles on Friday, and 68 miles on Saturday. What was the total number of miles Ethan rode?
- Business Chloe has a flower shop. Last week she made 19 floral arrangements on Monday, 12 on Tuesday, 23 on Wednesday, 29 on Thursday, and 44 on Friday. What was the total number of floral arrangements Chloe made?
- Apartment size Jackson lives in a 7 room apartment. The number of square feet in each room is 238, 120, 156, 196, 100, 132, and 225. What is the total number of square feet in all 7 rooms?
- Weight Seven men rented a fishing boat. The weights of the men were 175, 192, 148, 169, 205, 181, and 225 pounds. What was the total weight of the seven men?
- Salary Last year Natalie’s salary was $82,572. Two years ago, her salary was $79,316, and three years ago it was $75,298. What is the total amount of Natalie’s salary for the past three years?
- Home sales Emma is a realtor. Last month, she sold three houses. The selling prices of the houses were $292,540, $505,875, and $423,699. What was the total of the three selling prices?
In the following exercises, find the perimeter of each figure.
Everyday Math
- Calories Paulette had a grilled chicken salad, ranch dressing, and a 16-ounce drink for lunch. On the restaurant’s nutrition chart, she saw that each item had the following number of calories: Grilled chicken salad – 320 calories, Ranch dressing – 170 calories, 16-ounce drink – 150 calories. What was the total number of calories of Paulette’s lunch?
- Calories Fred had a grilled chicken sandwich, a small order of fries, and a 12-oz chocolate shake for dinner. The restaurant’s nutrition chart lists the following calories for each item: Grilled chicken sandwich – 420 calories, Small fries – 230 calories, 12-oz chocolate shake – 580 calories. What was the total number of calories of Fred’s dinner?
- Test scores A students needs a total of 400 points on five tests to pass a course. The student scored 82, 91, 75, 88, and 70. Did the student pass the course?
- Elevators The maximum weight capacity of an elevator is 1150 pounds. Six men are in the elevator. Their weights are 210, 145, 183, 230, 159, and 164 pounds. Is the total weight below the elevators’ maximum capacity?
Writing Exercises
- How confident do you feel about your knowledge of the addition facts? If you are not fully confident, what will you do to improve your skills?
- How have you used models to help you learn the addition facts?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) After reviewing this checklist, what will you do to become confident for all objectives?
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.