1.5: Subtraction of Whole Numbers

Last updated
Save as PDF

Page ID: 48778

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

understand the subtraction process
be able to subtract whole numbers
be able to use a calculator to subtract one whole number from another whole number

Subtraction

Definition: Subtraction

Subtraction is the process of determining the remainder when part of the total is removed.

Suppose the sum of two whole numbers is 11, and from 11 we remove 4. Using the number line to help our visualization, we see that if we are located at 11 and move 4 units to the left, and thus remove 4 units, we will be located at 7. Thus, 7 units remain when we remove 4 units from 11 units.

$A number line, with an arrow, labeled -4, drawn from the mark for 11 to the mark for 7.$

Definition: The Minus Symbol

The minus symbol (-) is used to indicate subtraction. For example, 11 − 4 indicates that 4 is to be subtracted from 11.

Definition: Minuend

The number immediately in front of or the minus symbol is called the minuend, and it represents the original number of units.

Definition: Subtrahend

The number immediately following or below the minus symbol is called the subtrahend, and it represents the number of units to be removed.

Definition: Difference

The result of the subtraction is called the difference of the two numbers. For example, in 11 − 4 = 7

Subtraction as the Opposite of Addition

Subtraction can be thought of as the opposite of addition. We show this in the problems in Sample Set A.

Sample Set A

8 - 5 = 3 since 3 + 5 = 8.

Sample Set A

9 - 3 = 6 since 6 + 3 = 9.

Practice Set A

Complete the following statements.

7 - 5 = since + 5 = 7

Answer: 7 - 5 = 2 since 2 + 5 = 7

Practice Set A

9 - 1 = since + 1 = 9

Answer: 9 - 1 = 8 since 8 + 1 = 9

Practice Set A

17 - 8 = since + 8 = 17

Answer: 17 - 8 = 9 since 9 + 8 = 17

The Subtraction Process

We'll study the process of the subtraction of two whole numbers by considering the difference between 48 and 35.

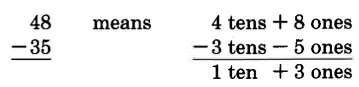
$Vertical subtraction. 48 - 35 means, 4 tens + 8 ones, minus 3 tens - 5 ones = 1 ten + 3 ones.$

which we write as 13.

The Process of Subtracting Whole Numbers

To subtract two whole numbers,

The process

Write the numbers vertically, placing corresponding positions in the same column.
$\begin{array} {r} {48} \\ {\underline{-35}} \end{array}$
Subtract the digits in each column. Start at the right, in the ones position, and move to the left, placing the difference at the bottom.
$\begin{array} {r} {48} \\ {\underline{-35}} \\ {13} \end{array}$

Sample Set B

Perform the following subtractions.

$\begin{array} {r} {275} \\ {\underline{-142}} \\ {133} \end{array}$

$\begin{array} {l} {5 - 2 = 3.} \\ {7 - 4 = 3.} \\ {2 - 1 = 1.} \end{array}$

Sample Set B

$\begin{array} {r} {46,042} \\ {\underline{-\ \ 1,031}} \\ {45,011} \end{array}$

$\begin{array} {l} {2 - 1 = 1.} \\ {4 - 3 = 1.} \\ {0 - 0 = 0.} \\ {6 - 1 = 5.} \\ {4 - 0 = 4.} \end{array}$

Sample Set B

Find the difference between 977 and 235.

Write the numbers vertically, placing the larger number on top. Line up the columns properly.

$\begin{array} {r} {977} \\ {\underline{-235}} \\ {742} \end{array}$

The difference between 977 and 235 is 742.

Sample Set B

In Keys County in 1987, there were 809 cable television installations. In Flags County in 1987, there were 1,159 cable television installations. How many more cable television installations were there in Flags County than in Keys County in 1987?

We need to determine the difference between 1,159 and 809.

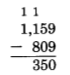
$1,159 - 809 = 350, with a 1 above the thousands and hundreds columns.$

There were 350 more cable television installations in Flags County than in Keys County in 1987.

Practice Set B

Perform the following subtractions.

$\begin{array} {r} {534} \\ {\underline{-203}} \end{array}$

Answer: 331

Practice Set B

$\begin{array} {r} {857} \\ {\underline{-\ \ 43}} \end{array}$

Answer: 814

Practice Set B

$\begin{array} {r} {95,628} \\ {\underline{-34,510}} \end{array}$

Answer: 61,118

Practice Set B

$\begin{array} {r} {11,005} \\ {\underline{-\ \ 1,005}} \end{array}$

Answer: 10,000

Practice Set B

Find the difference between 88,526 and 26,412.

Answer: 62,114

In each of these problems, each bottom digit is less than the corresponding top digit. This may not always be the case. We will examine the case where the bottom digit is greater than the corresponding top digit in the next section.

Subtraction Involving Borrowing

Definition: Minuend and Subtrahend

It often happens in the subtraction of two whole numbers that a digit in the minuend (top number) will be less than the digit in the same position in the subtrahend (bottom number). This happens when we subtract 27 from 84.

$\begin{array} {r} {84} \\ {\underline{-27}} \end{array}$

We do not have a name for 4 − 7. We need to rename 84 in order to continue. We'll do so as follows:

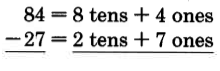
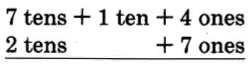
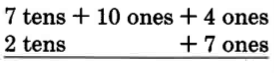
$Vertical subtraction. 84 - 27 is equal to 8 tens + 4 ones, over 2 tens + 7 ones.$ $Vertical subtraction. 7 tens + 1 ten + 4 ones, over 2 tens + 7 ones.$ $Vertical subtraction. 7 tens + 10 ones + 4 ones, over 2 tens + 7 ones.$

Our new name for 84 is 7 tens + 14 ones.

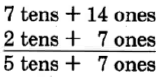
$Vertical subtraction. 7 tens + 14 ones, over 2 tens + 7 ones = 5 tens + 7 ones.$

= 57

Notice that we converted 8 tens to 7 tens + 1 ten, and then we converted the 1 ten to 10 ones. We then had 14 ones and were able to perform the subtraction.

Definition: Borrowing

The process of borrowing (converting) is illustrated in the problems of Sample Set C.

Sample Set C

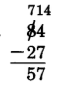
$84 - 27 = 57. The 8 in 84 is crossed out, with a 7 above it. There is a 14 above the ones column.$

Borrow 1 ten from the 8 tens. This leaves 7 tens.
Convert the 1 ten to 10 ones.
Add 10 ones to 4 ones to get 14 ones.

Sample Set C

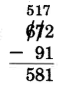
$672 - 91 = 581. The 6 in 672 is crossed out, with a 5 above it. The 7 in 672 is crossed out, with 17 above it.$

Borrow 1 hundred from the 6 hundreds. This leaves 5 hundreds.
Convert the 1 hundred to 10 tens.
Add 10 tens to 7 tens to get 17 tens.

Practice Set C

Perform the following subtractions. Show the expanded form for the first three problems.

$\begin{array} {r} {53} \\ {\underline{-35}} \end{array}$

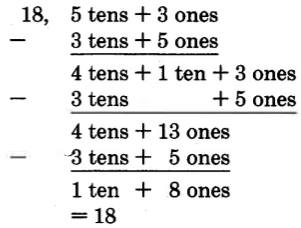
Answer: $The solution is 18. The subtraction can be broken into the quantity 5 tens + 3 ones, minus the quantity 3 tens + 5 ones. 5 tens + 3 ones can be broken down to 4 tens + 1 ten + 3 ones, or 4 tens + 13 ones. The difference is 1 ten + 8 ones, or 18.$

Practice Set C

$\begin{array} {r} {76} \\ {\underline{-28}} \end{array}$

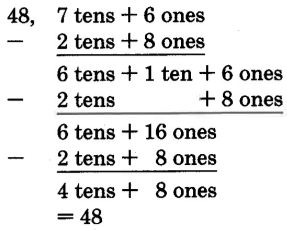
Answer: $The solution is 48. The subtraction problem can be expanded to the quantity 7 tens + 6 ones, minus the quantity 2 tens + 8 ones. 7 tens + 6 ones can be expanded to be 6 tens + 1 ten + 6 ones, or 6 tens + 16 ones. The sum becomes 4 tens + 8 ones, or 48.$

Practice Set C

$\begin{array} {r} {872} \\ {\underline{-565}} \end{array}$

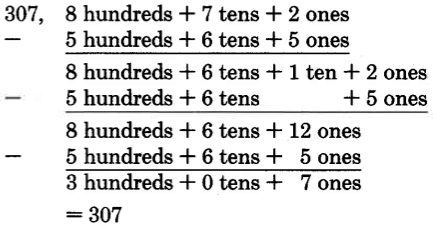
Answer: $The solution is 307. The subtraction problem can be expanded to be the quantity, 8 hundreds + 7 tens + 2 ones, minus the quantity, 5 hundreds + 6 tens + 5 ones. 8 hundreds + 7 tens + 2 ones can be expanded to 8 hundreds + 6 tens + 1 ten + 2 ones, or 8 hundreds + 6 tens + 12 ones. The difference is 3 hundreds + 0 tens + 7 ones, or 307.$

Practice Set C

$\begin{array} {r} {441} \\ {\underline{-356}} \end{array}$

Answer: 85

Practice Set C

$\begin{array} {r} {775} \\ {\underline{-\ \ 66}} \end{array}$

Answer: 709

Practice Set C

$\begin{array} {r} {5,663} \\ {\underline{-2,559}} \end{array}$

Answer: 3,104

Borrowing More Than Once

Sometimes it is necessary to borrow more than once. This is shown in the problems in Sample Set D.

Sample Set D

Perform the Subtractions. Borrowing more than once if necessary

$641 - 358 = 283. the 4 in 641 is crossed out, with a 3 marked above it. Above the 1 in 641 is 11. The 6 in 641 is then crossed out, with a 5 marked above it. The 3 above the 4 is crossed out, with a 13 marked above it.$

Borrow 1 ten from the 4 tens. This leaves 3 tens.
Convert the 1 ten to 10 ones.
Add 10 ones to 1 one to get 11 ones. We can now perform 11 − 8.
Borrow 1 hundred from the 6 hundreds. This leaves 5 hundreds.
Convert the 1 hundred to 10 tens.
Add 10 tens to 3 tens to get 13 tens.
Now 13 − 5 = 8.
5 − 3 = 2.

Sample Set D

$534 - 85 = 449. The 3 in 534 is crossed out, with a 2 above it. Above the 4 is a 14. The 5 in 534 is then crossed out, with a 4 marked above it. The 2 above the 3 in 534 is crossed out, with a 12 above it.$

Borrow 1 ten from the 3 tens. This leaves 2 tens.
Convert the 1 ten to 10 ones.
Add 10 ones to 4 ones to get 14 ones. We can now perform 14 − 5.
Borrow 1 hundred from the 5 hundreds. This leaves 4 hundreds.
Convert the 1 hundred to 10 tens.
Add 10 tens to 2 tens to get 12 tens. We can now perform 12 − 8 = 4.
Finally, 4 − 0 = 4.

Sample Set D

$\begin{array} {r} {71529} \\ {\underline{-\ \ 6952}} \end{array}$

After borrowing, we have

$71529 - 6952 = 64577. Above the 5 is a 4, and above the 2 is a 12. Above the 1 is a 0, and above the 7 is a 6. The 0 and the 4 are crossed out, with a 14 written above the 4, and a 10 written above the 0.$

Practice Set D

Perform the following subtractions.

$\begin{array} {r} {526} \\ {\underline{-358}} \end{array}$

Answer: 168

Practice Set D

$\begin{array} {r} {63,419} \\ {\underline{-\ \ 7,779}} \end{array}$

Answer: 55,640

Practice Set D

$\begin{array} {r} {4,312} \\ {\underline{-3,123}} \end{array}$

Answer: 1,189

Borrowing from Zero

It often happens in a subtraction problem that we have to borrow from one or more zeros. This occurs in problems such as

$\begin{array} {r} {503} \\ {\underline{-\ \ 37}} \\ {\text{and}\ \ \ \ } \\ {5000} \\ {\underline{-\ \ \ \ 37}} \end{array}$

We'll examine each case.

Borrowing from a single zero.

Consider the problem $\begin{array} {r} {503} \\ {\underline{-\ \ 37}} \end{array}$

Since we do not have a name for 3 − 7, we must borrow from 0.

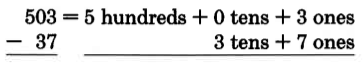
$Vertical subtraction. 503 - 37 is equal to 5 hundreds + 0 tens + 3 ones, minus 3 tens + 7 ones.$

Since there are no tens to borrow, we must borrow 1 hundred. One hundred = 10 tens.

$Vertical subtraction. 4 hundreds + 10 tens + 3 ones, minus 3 tens + 7 ones.$

We can now borrow 1 ten from 10 tens (leaving 9 tens). One ten = 10 ones and 10 ones + 3 ones = 13 ones.

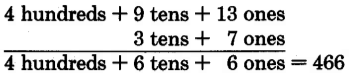
$Vertical subtraction. 4 hundreds + 9 tens + 13 ones, minus 3 tens + 7 ones = 4 hundreds + 6 tens + 6 ones, equal to 466.$

Now we can suggest the following method for borrowing from a single zero.

Borrowing from a Single Zero To borrow from a single zero,

Decrease the digit to the immediate left of zero by one.
Draw a line through the zero and make it a 10.
Proceed to subtract as usual.

Sample Set E

Perform this subtraction.

$\begin{array} {r} {503} \\ {\underline{-\ \ 37}} \end{array}$

The number 503 contains a single zero

The number to the immediate left of 0 is 5. Decrease 5 by 1.
5 - 1 = 4
$503 - 37. The 5 is crossed out, with a 4 above it. The 0 is crossed out, with a 10 above it.$
Draw a line through the zero and make it a 10.
Borrow from the 10 and proceed. $503 - 37. The 5 is crossed out, with a 4 above it. The 0 is crossed out, with a 10 above it. The 10 is crossed out, with a 9 above it. The 3 is crossed out, with a 13 above it. The difference is 466.$
$\begin{array} {l} {\text{1 ten + 10 ones}} \\ {\text{10 ones + 3 ones = 13 ones}} \end{array}$

Practice Set E

Perform each subtraction.

$\begin{array} {r} {906} \\ {\underline{-\ \ 18}} \end{array}$

Answer: 888

Practice Set E

$\begin{array} {r} {5102} \\ {\underline{-\ \ 559}} \end{array}$

Answer: 4,543

Practice Set E

$\begin{array} {r} {9055} \\ {\underline{-\ \ 386}} \end{array}$

Answer: 8,669

Borrowing from a group of zeros

Consider the problem $\begin{array} {r} {5000} \\ {\underline{-\ \ \ \ 37}} \end{array}$

In this case, we have a group of zeros.

$Vertical subtraction. 5000 - 37 is equal to 5 thousands + 0 hundred + 0 tens + 0 ones, minus 3 tens + 7 ones.$

Since we cannot borrow any tens or hundreds, we must borrow 1 thousand. One thousand = 10 hundreds.

$Vertical subtraction. 4 thousands + 10 hundreds + 0 tens + 0 ones, minus 3 tens + 7 ones.$

We can now borrow 1 hundred from 10 hundreds. One hundred = 10 tens.

$Vertical subtraction. 4 thousands + 9 hundreds + 10 tens + 0 ones, minus 3 tens + 7 ones.$

We can now borrow 1 ten from 10 tens. One ten = 10 ones.

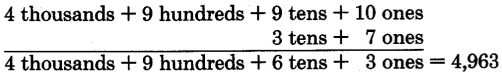
$Vertical subtraction. 4 thousands + 9 hundreds + 9 tens + 10 ones, minus 3 tens + 7 ones = 4 thousands + 9 hundreds + 6 tens + 3 ones, equal to 4,963$

From observations made in this procedure we can suggest the following method for borrowing from a group of zeros.

Borrowing from a Group of zeros

To borrow from a group of zeros,

Decrease the digit to the immediate left of the group of zeros by one.
Draw a line through each zero in the group and make it a 9, except the rightmost zero, make it 10.
Proceed to subtract as usual.

Sample Set F

Perform each subtraction.

$\begin{array} {r} {40,000} \\ {\underline{-\ \ \ \ \ 125}} \end{array}$

Solution

The number 40,000 contains a group of zeros.

The number to the immediate left of the group is 4. Decrease 4 by 1.
4 - 1 = 3
Make each 0, except the rightmost one, 9. Make the rightmost 0 a 10. $40,000 - 125. Each digit of 40,000 is crossed out, and above it from left to right are the numbers, 3, 9, 9, 9, and 10.$
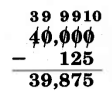
Subtract as usual. $40,000 - 125. Each digit of 40,000 is crossed out, and above it from left to right are the numbers, 3, 9, 9, 9, and 10. The difference is 39,875.$

Example $\PageIndex{1}$

$\begin{array} {r} {8,000,006} \\ {\underline{-\ \ \ \ \ 41,107}} \end{array}$

Solution

The number 8,000,006 contains a group of zeros.

The number to the immediate left of the group is 8. Decrease 8 by 1.
8 - 1 = 7
Make each zero, except the rightmost one, 9. Make the rightmost 0 a 10. $8,000,006 - 41,107. All but the ones digit are crossed out, and above them from left to right are 7, 9, 9, 9, 9, and 10.$
To perform the subtraction, we’ll need to borrow from the ten. $8,000,006 - 41,107. All but the ones digit are crossed out, and above them from left to right are 7, 9, 9, 9, 9, and 10. The 10 is crossed out, with a 9 above it. Above the 6 is a 16. The difference is 7,958,899.$
$\begin{array} {l} {\text{1 ten = 10 ones}} \\ {\text{10 ones + 6 ones = 16 ones}} \end{array}$

Practice Set F

Perform each subtraction.

$\begin{array} {r} {21,007} \\ {\underline{-\ \ 4,873}} \end{array}$

Answer: 16,134

Practice Set F

$\begin{array} {r} {10,004} \\ {\underline{-\ \ 5,165}} \end{array}$

Answer: 4,839

Practice Set F

$\begin{array} {r} {16,000,000} \\ {\underline{-\ \ \ \ \ 201,060}} \end{array}$

Answer: 15,789,940

Calculators

In practice, calculators are used to find the difference between two whole numbers.

Sample Set G

Find the difference between 1006 and 284.

Display Reads
Type	1006	1006
Press	−−	1006
Type	284	284
Press	=	722

The difference between 1006 and 284 is 722.

(What happens if you type 284 first and then 1006? We'll study such numbers in Chapter 10.)

Practice Set G

Use a calculator to find the difference between 7338 and 2809.

Answer: 4,529

Practice Set G

Use a calculator to find the difference between 31,060,001 and 8,591,774.

Answer: 22,468,227

Exercises

For the following problems, perform the subtractions. You may check each difference with a calculator.

Exercise $\PageIndex{1}$

$\begin{array} {r} {15} \\ {\underline{-\ \ 8}} \end{array}$

Answer: 7

Exercise $\PageIndex{2}$

$\begin{array} {r} {19} \\ {\underline{-\ \ 8}} \end{array}$

Exercise $\PageIndex{3}$

$\begin{array} {r} {11} \\ {\underline{-\ \ 5}} \end{array}$

Answer: 6

Exercise $\PageIndex{4}$

$\begin{array} {r} {14} \\ {\underline{-\ \ 6}} \end{array}$

Exercise $\PageIndex{5}$

$\begin{array} {r} {12} \\ {\underline{-\ \ 9}} \end{array}$

Answer: 3

Exercise $\PageIndex{6}$

$\begin{array} {r} {56} \\ {\underline{-12}} \end{array}$

Exercise $\PageIndex{7}$

$\begin{array} {r} {74} \\ {\underline{-33}} \end{array}$

Answer: 41

Exercise $\PageIndex{8}$

$\begin{array} {r} {80} \\ {\underline{-61}} \end{array}$

Exercise $\PageIndex{9}$

$\begin{array} {r} {350} \\ {\underline{-141}} \end{array}$

Answer: 209

Exercise $\PageIndex{10}$

$\begin{array} {r} {800} \\ {\underline{-650}} \end{array}$

Exercise $\PageIndex{11}$

$\begin{array} {r} {35,002} \\ {\underline{-14,001}} \end{array}$

Answer: 21,001

Exercise $\PageIndex{12}$

$\begin{array} {r} {5,000,566} \\ {\underline{-2,441,326}} \end{array}$

Exercise $\PageIndex{13}$

$\begin{array} {r} {400,605} \\ {\underline{-121,352}} \end{array}$

Answer: 279,253

Exercise $\PageIndex{14}$

$\begin{array} {r} {46,400} \\ {\underline{-\ \ 2,012}} \end{array}$

Exercise $\PageIndex{15}$

$\begin{array} {r} {77,893} \\ {\underline{-\ \ \ \ \ 421}} \end{array}$

Answer: 77,472

Exercise $\PageIndex{16}$

$\begin{array} {r} {42} \\ {\underline{-18}} \end{array}$

Exercise $\PageIndex{17}$

$\begin{array} {r} {51} \\ {\underline{-27}} \end{array}$

Answer: 24

Exercise $\PageIndex{18}$

$\begin{array} {r} {622} \\ {\underline{-\ \ 88}} \end{array}$

Exercise $\PageIndex{19}$

$\begin{array} {r} {261} \\ {\underline{-\ \ 73}} \end{array}$

Answer: 188

Exercise $\PageIndex{20}$

$\begin{array} {r} {242} \\ {\underline{-158}} \end{array}$

Exercise $\PageIndex{21}$

$\begin{array} {r} {3,422} \\ {\underline{-1,045}} \end{array}$

Answer: 2,377

Exercise $\PageIndex{22}$

$\begin{array} {r} {5,565} \\ {\underline{-3,985}} \end{array}$

Exercise $\PageIndex{23}$

$\begin{array} {r} {42,041} \\ {\underline{-15,355}} \end{array}$

Answer: 26,686

Exercise $\PageIndex{24}$

$\begin{array} {r} {304,056} \\ {\underline{-\ \ 20,008}} \end{array}$

Exercise $\PageIndex{25}$

$\begin{array} {r} {64,000,002} \\ {\underline{-\ \ \ \ \ 856,743}} \end{array}$

Answer: 63,143,259

Exercise $\PageIndex{26}$

$\begin{array} {r} {4,109} \\ {\underline{-\ \ \ 856}} \end{array}$

Exercise $\PageIndex{27}$

$\begin{array} {r} {10,113} \\ {\underline{-\ \ 2,079}} \end{array}$

Answer: 8,034

Exercise $\PageIndex{28}$

$\begin{array} {r} {605} \\ {\underline{-\ \ 77}} \end{array}$

Exercise $\PageIndex{27}$

$\begin{array} {r} {59} \\ {\underline{-26}} \end{array}$

Answer: 33

Exercise $\PageIndex{28}$

$\begin{array} {r} {36,107} \\ {\underline{-\ \ 8,314}} \end{array}$

Exercise $\PageIndex{29}$

$\begin{array} {r} {92,526,441,820} \\ {\underline{-59,914,805,253}} \end{array}$

Answer: 32,611,636,567

Exercise $\PageIndex{30}$

$\begin{array} {r} {1,605} \\ {\underline{-\ \ 881}} \end{array}$

Exercise $\PageIndex{31}$

$\begin{array} {r} {30,000} \\ {\underline{-26,062}} \end{array}$

Answer: 3,938

Exercise $\PageIndex{32}$

$\begin{array} {r} {600} \\ {\underline{-216}} \end{array}$

Exercise $\PageIndex{33}$

$\begin{array} {r} {90,000,003} \\ {\underline{-\ \ \ 726,048}} \end{array}$

Answer: 8,273,955

For the following problems, perform each subtraction.

Exercise $\PageIndex{34}$

Subtract 63 from 92.

Hint:

The word "from" means "beginning at." Thus, 63 from 92 means beginning at 92, or 92 - 63.

Exercise $\PageIndex{35}$

Subtract 35 from 86.

Answer: 51

Exercise $\PageIndex{34}$

Subtract 382 from 541.

Exercise $\PageIndex{35}$

Subtract 1,841 from 5,246.

Answer: 3,405

Exercise $\PageIndex{36}$

Subtract 26,082 from 35,040.

Exercise $\PageIndex{37}$

Find the difference between 47 and 21.

Answer: 26

Exercise $\PageIndex{38}$

Find the difference between 1,005 and 314.

Exercise $\PageIndex{39}$

Find the difference between 72,085 and 16.

Answer: 72,069

Exercise $\PageIndex{40}$

Find the difference between 7,214 and 2,049.

Exercise $\PageIndex{41}$

Find the difference between 56,108 and 52,911.

Answer: 3,197

Exercise $\PageIndex{42}$

How much bigger is 92 than 47?

Exercise $\PageIndex{43}$

How much bigger is 114 than 85?

Answer: 29

Exercise $\PageIndex{44}$

How much bigger is 3,006 than 1,918?

Exercise $\PageIndex{45}$

How much bigger is 11,201 than 816?

Answer: 10,385

Exercise $\PageIndex{46}$

How much bigger is 3,080,020 than 1,814,161?

Exercise $\PageIndex{47}$

In Wichita, Kansas, the sun shines about 74% of the time in July and about 59% of the time in November. How much more of the time (in percent) does the sun shine in July than in November?

Answer: 15%

Exercise $\PageIndex{48}$

The lowest temperature on record in Concord, New Hampshire in May is 21°F, and in July it is 35°F. What is the difference in these lowest temperatures?

Exercise $\PageIndex{49}$

In 1980, there were 83,000 people arrested for prostitution and commercialized vice and 11,330,000 people arrested for driving while intoxicated. How many more people were arrested for drunk driving than for prostitution?

Answer: 11,247,000

Exercise $\PageIndex{50}$

In 1980, a person with a bachelor's degree in accounting received a monthly salary offer of $1,293, and a person with a marketing degree a monthly salary offer of $1,145. How much more was offered to the person with an accounting degree than the person with a marketing degree?

Exercise $\PageIndex{51}$

In 1970, there were about 793 people per square mile living in Puerto Rico, and 357 people per square mile living in Guam. How many more people per square mile were there in Puerto Rico than Guam?

Answer: 436

Exercise $\PageIndex{52}$

The 1980 population of Singapore was 2,414,000 and the 1980 population of Sri Lanka was 14,850,000. How many more people lived in Sri Lanka than in Singapore in 1980?

Exercise $\PageIndex{53}$

In 1977, there were 7,234,000 hospitals in the United States and 64,421,000 in Mainland China. How many more hospitals were there in Mainland China than in the United States in 1977?

Answer: 57,187,000

Exercise $\PageIndex{54}$

In 1978, there were 3,095,000 telephones in use in Poland and 4,292,000 in Switzerland. How many more telephones were in use in Switzerland than in Poland in 1978?

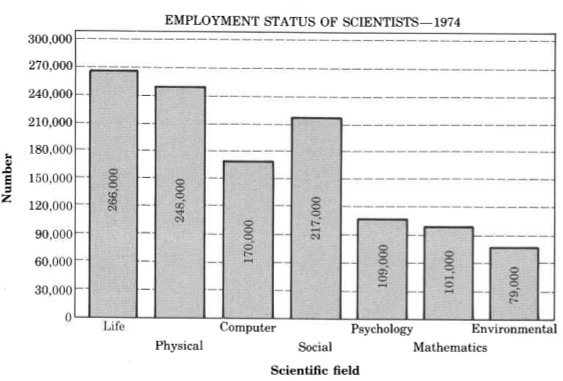
For the following problems, use the corresponding graphs to solve the problems.

Exercise $\PageIndex{55}$

How many more life scientists were there in 1974 than mathematicians?

Answer: 165,000

Exercise $\PageIndex{56}$

How many more social, psychological, mathematical, and environmental scientists were there than life, physical, and computer scientists?

$A graph entitled employment status of mathematical scientists - 1974. On the graph are histograms with scientific field titles, and a labeled number of the scientists holding the titles. There are 266,000 life scientists, 248,000 physical scientists, 170,000 computer scientists, 217,000 social scientists, 109,000 psychologists, 101,000, mathematicians, and 79,000 environmental scientists.$

Exercise $\PageIndex{57}$

How many more prosecutions were there in 1978 than in 1974?

Answer: 74

Exercise $\PageIndex{58}$

How many more prosecutions were there in 1976-1980 than in 1970-1975?

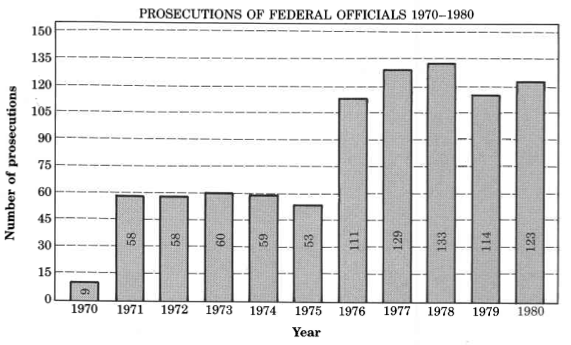
$A graph entitled prosecutions of federal officials 1970-1980, with histograms of the years on the horizontal axis, and number of prosecutions on the vertical axis. The years in ascending succession had the following number of prosecutions, 9, 58, 58, 60, 59, 53, 111, 129, 133, 114, 123.$

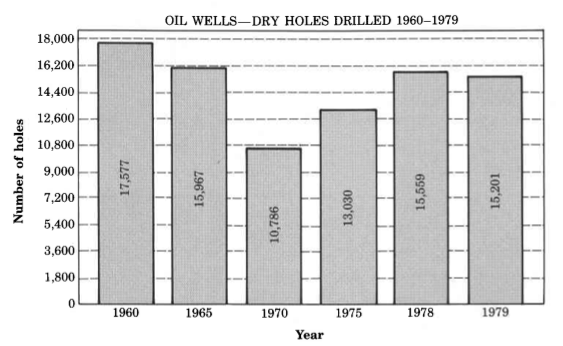
Exercise $\PageIndex{59}$

How many more dry holes were drilled in 1960 than in 1975?

Answer: 4,547

Exercise $\PageIndex{60}$

How many more dry holes were drilled in 1960, 1965, and 1970 than in 1975, 1978 and 1979?

$A graph entitled, oil wells - dry holes drilled 1960-1979. The histograms of the years in the period are displayed along the horizontal axis. The number of holes are measured on the vertical axis. The number of holes drilled, for each consecutive year 1960, 1965, 1970, 1975, 1978, and 1979, are 17,577, 15,967, 10,786, 13,030, 15,559, 15,201.$

For the following problems, replace the ☐ with the whole number that will make the subtraction true.

Exercise $\PageIndex{61}$

$\begin{array} {r} {14} \\ {\underline{-☐}} \\ {3} \end{array}$

Answer: 11

Exercise $\PageIndex{62}$

$\begin{array} {r} {21} \\ {\underline{-☐}} \\ {14} \end{array}$

Exercise $\PageIndex{63}$

$\begin{array} {r} {35} \\ {\underline{-☐}} \\ {25} \end{array}$

Answer: 10

Exercise $\PageIndex{64}$

$\begin{array} {r} {16} \\ {\underline{-☐}} \\ {9} \end{array}$

Exercise $\PageIndex{65}$

$\begin{array} {r} {28} \\ {\underline{-☐}} \\ {16} \end{array}$

Answer: 12

For the following problems, find the solutions.

Exercise $\PageIndex{66}$

Subtract 42 from the sum of 16 and 56.

Exercise $\PageIndex{67}$

Subtract 105 from the sum of 92 and 89.

Answer: 76

Exercise $\PageIndex{68}$

Subtract 1,127 from the sum of 2,161 and 387.

Exercise $\PageIndex{69}$

Subtract 37 from the difference between 263 and 175.

Answer: 51

Exercise $\PageIndex{70}$

Subtract 1,109 from the difference between 3,046 and 920.

Exercise $\PageIndex{71}$

Add the difference between 63 and 47 to the difference between 55 and 11.

Answer: 60

Exercise $\PageIndex{72}$

Add the difference between 815 and 298 to the difference between 2,204 and 1,016.

Exercise $\PageIndex{73}$

Subtract the difference between 78 and 43 from the sum of 111 and 89.

Answer: 165

Exercise $\PageIndex{74}$

Subtract the difference between 18 and 7 from the sum of the differences between 42 and 13, and 81 and 16.

Exercise $\PageIndex{75}$

Find the difference between the differences of 343 and 96, and 521 and 488.

Answer: 214

Exercises for Review

Exercise $\PageIndex{76}$

In the number 21,206, how many hundreds are there?

Exercise $\PageIndex{77}$

Write a three-digit number that has a zero in the ones position.

Answer: 330 (answers may vary)

Exercise $\PageIndex{78}$

How many three-digit whole numbers are there?

Exercise $\PageIndex{79}$

Round 26,524,016 to the nearest million.

Answer: 27,000,000

Exercise $\PageIndex{80}$

Find the sum of 846 + 221 + 116.