7.4: Percent

Last updated
Save as PDF

Page ID: 48874

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

understand the relationship between ratios and percents
be able to make conversions between fractions, decimals, and percents

Ratios and Percents

Ratio, Percent
We defined a ratio as a comparison, by division, of two pure numbers or two like denominate numbers. A most convenient number to compare numbers to is 100. Ratios in which one number is compared to 100 are called percents. The word percent comes from the Latin word "per centum." The word "per" means "for each" or "for every," and the word "centum" means "hundred." Thus, we have the following definition.

Percent means “for each hundred," or "for every hundred."

The symbol % is used to represent the word percent.

Sample Set A

The ratio 26 to 100 can be written as 26%. We read 26% as "twenty-six percent."

Sample Set A

The ratio $\dfrac{165}{100}$ can be written as 165%.

We read 165% as "one hundred sixty-five percent."

Sample Set A

The percent 38% can be written as the fraction $\dfrac{38}{100}$.

Sample Set A

The percent 210% can be written as the fraction $\dfrac{210}{100}$ or the mixed number $2\dfrac{1)}{100}$ or 2.1.

Sample Set A

Since one dollar is 100 cents, 25 cents is $\dfrac{25}{100}$ of a dollar. This implies that 25 cents is 25% of one dollar.

Practice Set A

Write the ratio 16 to 100 as a percent.

Answer: 16%

Practice Set A

Write the ratio 195 to 100 as a percent.

Answer: 195%

Practice Set A

Write the percent 83% as a ratio in fractional form.

Answer: $\dfrac{83}{100}$

Practice Set A

Write the percent 362% as a ratio in fractional form.

Answer: $\dfrac{362}{100}$ or $\dfrac{181}{50}$

The Relationship Between Fractions, Decimals, and Percents – Making Conversions

Since a percent is a ratio, and a ratio can be written as a fraction, and a fraction can be written as a decimal, any of these forms can be converted to any other.

Before we proceed to the problems in Sample Set B and Practice Set B, let's summarize the conversion techniques.

Conversion Techniques – Fractions, Decimals, Percents
To Convert a Fraction	To Convert a Decimal	To Convert a Percent
To a decimal: Divide the numerator by the denominator	To a fraction: Read the decimal and reduce the resulting fraction	To a decimal: Move the decimal point 2 places to the left and drop the % symbol
To a percent: Convert the fraction first to a decimal, then move the decimal point 2 places to the right and affix the % symbol.	To a percent: Move the decimal point 2 places to the right and affix the % symbol	To a fraction: Drop the % sign and write the number “over” 100. Reduce, if possible.

Sample Set B

Convert 12% to a decimal.

Solution

$12\% = \dfrac{12}{100} = 0.12$

Note that

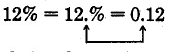
$Twelve percent is equal to .12. this diagram shows that the decimal place in 12% moves two spaces to the left to convert to a decimal.$

The % symbol is dropped, and the decimal point moves 2 places to the left.

Sample Set B

Convert 0.75 to a percent.

Solution

$0.75 = \dfrac{75}{100} = 75\%$

Note that

$.75 percent is equal to 75%. this diagram shows that the decimal place in .75 moves two spaces to the right to convert to a percent.$

The % symbol is affixed, and the decimal point moves 2 units to the right.

Sample Set B

Convert $\dfrac{3}{5}$ to a percent.

Solution

We see in Example above that we can convert a decimal to a percent. We also know that we can convert a fraction to a decimal. Thus, we can see that if we first convert the fraction to a decimal, we can then convert the decimal to a percent.

$\dfrac{3}{5} \to \begin{array} {r} {.6} \\ {5\overline{)3.0}} \\ {\underline{3\ 0}} \\ {0} \end{array} \text{ or } \dfrac{3}{5} = 0.6 = \dfrac{6}{10} = \dfrac{60}{100} = 60\%$

Sample Set B

Convert 42% to a fraction.

Solution

$42\% = \dfrac{42}{100} = \dfrac{21}{50}$

$42\% = 0.42 = \dfrac{42}{100} = \dfrac{21}{50}$

Practice Set B

Convert 21% to a decimal.

Answer: 0.21

Practice Set B

Convert 461% to a decimal.

Answer: 4.61

Practice Set B

Convert 0.55 to a percent.

Answer: 55%

Practice Set B

Convert 5.64 to a percent.

Answer: 564%

Practice Set B

Convert $\dfrac{3}{20}$ to a percent.

Answer: 15%

Practice Set B

Convert $\dfrac{11}{8}$ to a percent.

Answer: 137.5%

Practice Set B

Convert $\dfrac{3}{11}$ to a percent.

Answer: $27.\overline{27}$%

Exercises

For the following 12 problems, convert each decimal to a percent.

Exercise $\PageIndex{1}$

0.25

Answer: 25%

Exercise $\PageIndex{2}$

0.36

Exercise $\PageIndex{3}$

0.48

Answer: 48%

Exercise $\PageIndex{4}$

0.343

Exercise $\PageIndex{5}$

0.771

Answer: 77.1%

Exercise $\PageIndex{6}$

1.42

Exercise $\PageIndex{7}$

2.58

Answer: 258%

Exercise $\PageIndex{8}$

4.976

Exercise $\PageIndex{9}$

16.1814

Answer: 1,618.14%

Exercise $\PageIndex{10}$

533.01

Exercise $\PageIndex{11}$

Answer: 200%

Exercise $\PageIndex{12}$

For the following 10 problems, convert each percent to a decimal.

Exercise $\PageIndex{13}$

15%

Answer: 0.15

Exercise $\PageIndex{14}$

43%

Exercise $\PageIndex{15}$

16.2%

Answer: 0.162

Exercise $\PageIndex{16}$

53.8%

Exercise $\PageIndex{17}$

5.05%

Answer: 0.0505

Exercise $\PageIndex{18}$

6.11%

Exercise $\PageIndex{19}$

0.78%

Answer: 0.0078

Exercise $\PageIndex{20}$

0.88%

Exercise $\PageIndex{21}$

0.09%

Answer: 0.0009

Exercise $\PageIndex{22}$

0.001%

For the following 14 problems, convert each fraction to a percent.

Exercise $\PageIndex{23}$

$\dfrac{1}{5}$

Answer: 20%

Exercise $\PageIndex{24}$

$\dfrac{3}{5}$

Exercise $\PageIndex{25}$

$\dfrac{5}{8}$

Answer: 62.5%

Exercise $\PageIndex{26}$

$\dfrac{1}{16}$

Exercise $\PageIndex{27}$

$\dfrac{7}{25}$

Answer: 28%

Exercise $\PageIndex{28}$

$\dfrac{16}{45}$

Exercise $\PageIndex{29}$

$\dfrac{27}{55}$

Answer: $49.\overline{09}$%

Exercise $\PageIndex{30}$

$\dfrac{15}{8}$

Exercise $\PageIndex{31}$

$\dfrac{41}{25}$

Answer: 164%

Exercise $\PageIndex{32}$

$6 \dfrac{4}{5}$

Exercise $\PageIndex{33}$

$9 \dfrac{9}{20}$

Answer: 945%

Exercise $\PageIndex{34}$

$\dfrac{1}{200}$

Exercise $\PageIndex{35}$

$\dfrac{6}{11}$

Answer: $54.\overline{54}$%

Exercise $\PageIndex{36}$

$\dfrac{35}{27}$

For the following 14 problems, convert each percent to a fraction.

Exercise $\PageIndex{37}$

80%

Answer: $\dfrac{4}{5}$

Exercise $\PageIndex{38}$

60%

Exercise $\PageIndex{37}$

25%

Answer: $\dfrac{1}{4}$

Exercise $\PageIndex{38}$

75%

Exercise $\PageIndex{37}$

65%

Answer: $\dfrac{13}{20}$

Exercise $\PageIndex{38}$

18%

Exercise $\PageIndex{37}$

12.5%

Answer: $\dfrac{1}{8}$

Exercise $\PageIndex{38}$

37.5%

Exercise $\PageIndex{37}$

512.5%

Answer: $\dfrac{41}{8}$ or $5 \dfrac{1}{8}$

Exercise $\PageIndex{38}$

937.5%

Exercise $\PageIndex{37}$

$9.\overline{9}$%

Answer: $\dfrac{1}{10}$

Exercise $\PageIndex{38}$

$55.\overline{5}$%

Exercise $\PageIndex{37}$

$22.\overline{2}$%

Answer: $\dfrac{2}{9}$

Exercise $\PageIndex{38}$

$63.\overline{6}$%

Exercises for Review

Exercise $\PageIndex{39}$

Find the quotient. $\dfrac{40}{54} \div 8 \dfrac{7}{21}$.

Answer: $\dfrac{2}{9}$

Exercise $\PageIndex{40}$

$\dfrac{3}{8}$ of what number is $2\dfrac{2}{3}$?

Exercise $\PageIndex{41}$

Find the value of $\dfrac{28}{15} + \dfrac{7}{10} - \dfrac{5}{12}$.

Answer: $\dfrac{129}{60}$ or $2 \dfrac{9}{60} = 2 \dfrac{3}{20}$

Exercise $\PageIndex{42}$

Round 6.99997 to the nearest ten thousandths.

Exercise $\PageIndex{43}$

On a map, 3 inches represent 40 miles. How many inches represent 480 miles?

Answer: 36 inches

Search

Text Color

Text Size

Margin Size

Font Type

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set B

Sample Set B

Sample Set B

Sample Set B