2.1.2: Introducing Proportional Relationships with Tables

Lesson

Let's solve problems involving proportional relationships using tables.

Exercise \(\PageIndex{1}\): NOtice and Wonder: Paper Towels by The Case

Here is a table that shows how many rolls of paper towels a store receives when they order different numbers of cases.

Figure \(\PageIndex{1}\): Table with 2 columns and 4 rows of data. The columns are: number of cases they order and number of rolls of paper towels. The table has the ordered pairs ( 1 comma 12), (2 comma 36), (5 comma 60) and (10 comma 120). There is an arrow pointing from row 3 to row 4 on each side with times 2 next to the arrows.

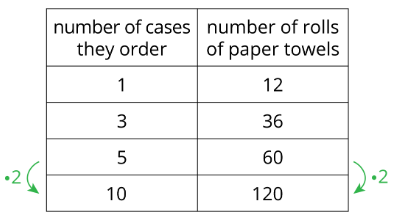
What do you notice about the table? What do you wonder?

Exercise \(\PageIndex{2}\): Feeding a Crowd

1. A recipe says that 2 cups of dry rice will serve 6 people. Complete the table as you answer the questions. Be prepared to explain your reasoning.
   1. How many people will 10 cups of rice serve?
   2. How many cups of rice are needed to serve 45 people?

      Table \(\PageIndex{1}\)

      cups of rice	number of people
      2	6
      3	9
      10
      	45

2. A recipe says that 6 spring rolls will serve 3 people. Complete the table.

   Table \(\PageIndex{2}\)

   number of spring rolls	number of people
   6	3
   30
   40
   	28

Exercise \(\PageIndex{3}\): Making Bread Dough

A bakery uses 8 tablespoons of honey for every 10 cups of flour to make bread dough. Some days they bake bigger batches and some days they bake smaller batches, but they always use the same ratio of honey to flour. Complete the table as you answer the questions. Be prepared to explain your reasoning.

1. How many cups of flour do they use with 20 tablespoons of honey?
2. How many cups of flour do they use with 13 tablespoons of honey?
3. How many tablespoons of honey do they use with 20 cups of flour?
4. What is the proportional relationship represented by this table?

Table \(\PageIndex{3}\)

honey (tbsp)	flour (c)
8	10
20
13
	20

Exercise \(\PageIndex{4}\): Quarters and Dimes

4 quarters are equal in value to 10 dimes.

1. How many dimes equal the value of 6 quarters?
2. How many dimes equal the value of 14 quarters?
3. What value belongs next to the 1 in the table? What does it mean in this context?

Table \(\PageIndex{4}\)

number of quarters	number of dimes
1
4	20
6
14

Are you ready for more?

Pennies made before 1982 are 95% copper and weigh about 3.11 grams each. (Pennies made after that date are primarily made of zinc). Some people claim that the value of the copper in one of these pennies is greater than the face value of the penny. Find out how much copper is worth right now, and decide if this claim is true.

Summary

If the ratios between two corresponding quantities are always equivalent, the relationship between the quantities is called a proportional relationship.

This table shows different amounts of milk and chocolate syrup. The ingredients in each row, when mixed together, would make a different total amount of chocolate milk, but these mixtures would all taste the same.

Table \(\PageIndex{5}\)

tablespoons of chocolate syrup	cups of milk
\(4\)	\(1\)
\(6\)	\(1\frac{1}{2}\)
\(8\)	\(2\)
\(\frac{1}{2}\)	\(\frac{1}{8}\)
\(12\)	\(3\)
\(1\)	\(\frac{1}{4}\)

Notice that each row in the table shows a ratio of tablespoons of chocolate syrup to cups of milk that is equivalent to \(4:1\).

About the relationship between these quantities, we could say:

• The relationship between amount of chocolate syrup and amount of milk is proportional.
• The relationship between the amount of chocolate syrup and the amount of milk is a proportional relationship.
• The table represents a proportional relationship between the amount of chocolate syrup and amount of milk.
• The amount of milk is proportional to the amount of chocolate syrup.

We could multiply any value in the chocolate syrup column by \(\frac{1}{4}\) to get the value in the milk column. We might call \(\frac{1}{4}\) a unit rate, because \(\frac{1}{4}\) cups of milk are needed for 1 tablespoon of chocolate syrup. We also say that \(\frac{1}{4}\) is the constant of proportionality for this relationship. It tells us how many cups of milk we would need to mix with 1 tablespoon of chocolate syrup.

Glossary Entries

Definition: Constant of Proportionality

In a proportional relationship, the values for one quantity are each multiplied by the same number to get the values for the other quantity. This number is called the constant of proportionality.

In this example, the constant of proportionality is 3, because \(2\cdot 3=6\), \(3\cdot 3=9\), and \(5\cdot 3=15\). This means that there are 3 apples for every 1 orange in the fruit salad.

Table \(\PageIndex{6}\)

number of oranges	number of apples
2	6
3	9
5	15

Definition: Equivalent Ratios

Two ratios are equivalent if you can multiply each of the numbers in the first ratio by the same factor to get the numbers in the second ratio. For example, \(8:6\) is equivalent to \(4:3\), because \(8\cdot\frac{1}{2}=4\) and \(6\cdot\frac{1}{2}=3\).

A recipe for lemonade says to use 8 cups of water and 6 lemons. If we use 4 cups of water and 3 lemons, it will make half as much lemonade. Both recipes taste the same, because and are equivalent ratios.

Table \(\PageIndex{7}\)

cups of water	number of lemons
8	6
4	3

Definition: Proportional Relationship

In a proportional relationship, the values for one quantity are each multiplied by the same number to get the values for the other quantity.

For example, in this table every value of \(p\) is equal to 4 times the value of \(s\) on the same row.

We can write this relationship as \(p=4s\). This equation shows that \(s\) is proportional to \(p\).

Table \(\PageIndex{8}\)

\(s\)	\(p\)
2	8
3	12
5	20
10	40

Practice

Exercise \(\PageIndex{5}\)

When Han makes chocolate milk, he mixes 2 cups of milk with 3 tablespoons of chocolate syrup. Here is a table that shows how to make batches of different sizes. Use the information in the table to complete the statements. Some terms are used more than once.

Figure \(\PageIndex{2}\): Table with 2 columns and 4 rows of data. The columns are: cups of milk and tablespoons of chocolate syrup. The table has the ordered pairs ( 2 comma 3), (8 comma 12), (1 comma the fraction 3 over 2) and (10 comma 15). There is an arrow pointing from row 1 to row 2 on each side with times 4 next to the arrows.

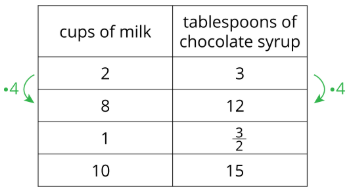
1. The table shows a proportional relationship between ______________ and ______________.
2. The scale factor shown is ______________.
3. The constant of proportionality for this relationship is______________.
4. The units for the constant of proportionality are ______________ per ______________.

Bank of Terms: tablespoons of chocolate syrup, 4, cups of milk, cup of milk, \(\frac{3}{2}\)

Exercise \(\PageIndex{6}\)

A certain shade of pink is created by adding 3 cups of red paint to 7 cups of white paint.

1. How many cups of red paint should be added to 1 cup of white paint?

   Table \(\PageIndex{9}\)

   cups of white paint	cups of red paint
   1
   7	3

2. What is the constant of proportionality?

Exercise \(\PageIndex{7}\)

A map of a rectangular park has a length of 4 inches and a width of 6 inches. It uses a scale of 1 inch for every 30 miles.

1. What is the actual area of the park? Show how you know.
2. The map needs to be reproduced at a different scale so that it has an area of 6 square inches and can fit in a brochure. At what scale should the map be reproduced so that it fits on the brochure? Show your reasoning.

(From Unit 1.2.6)

Exercise \(\PageIndex{8}\)

Noah drew a scaled copy of Polygon P and labeled it Polygon Q.

Figure \(\PageIndex{3}\): Polygon Q on a grid. Polygon Q has 8 sides. Starting at the bottom left corner, the first side is 9 units up, the second side is 6 units right, the third side is 3 units down, the fourth side is 3 units left, the fifth side is 3 units down, the sixth side is 3 units right, the seventh side is 3 units down, and the eighth side is 6 units left.

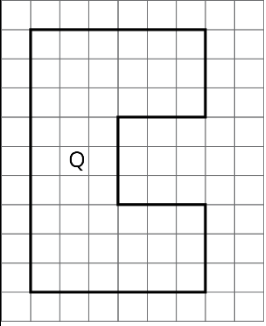
If the area of Polygon P is 5 square units, what scale factor did Noah apply to Polygon P to create Polygon Q? Explain or show how you know.

(From Unit 1.1.6)

Exercise \(\PageIndex{9}\)

Select all the ratios that are equivalent to each other.

1. \(4:7\)
2. \(8:15\)
3. \(16:28\)
4. \(2:3\)
5. \(20:35\)