3.6: Applications
- Page ID
- 22478
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Because we’ve increased our fundamental ability to simplify algebraic expressions, we’re now able to tackle a number of more advanced applications. Before we begin, we remind readers of required steps that must accompany solutions of applications.
- Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation. Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation. You must always solve the equation set up in the previous step.
- Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem.
- Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
Consecutive Integers
The integers are consecutive, in the sense that one follows right after another. For example, 5 and 6 are a pair of consecutive integers. The important relation to notice is the fact that the second integer of this pair is one larger than its predecessor. That is, 6 = 5 + 1.
Let k represent an integer. The next consecutive integer is the integer k + 1.
Thus, if k is an integer, then k + 1 is the next integer, k + 2 is the next integer after that, and so on.
The three sides of a triangle are consecutive integers and the perimeter is 72 inches. Find the measure of each side of the triangle.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. In this case, a carefully labeled diagram is the best way to indicate what the unknown variable represents.
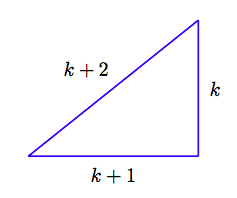
In our schematic diagram, we’ve labeled the three sides of the triangle with expressions representing the consecutive integers k, k+ 1, and k+ 2.
2. Set up an Equation. To find the perimeter P of the triangle, sum the three sides.
\[P = k + (k + 1) + (k + 2)\nonumber \]
However, we’re given the fact that the perimeter is 72 inches. Thus,
\[72 = k + (k + 1) + (k + 2)\nonumber \]
3. Solve the Equation. On the right, regroup and combine like terms.
\[72 = 3k + 3\nonumber \]
Now, solve.
\[ \begin{aligned} 72-3 = 3k + 3 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 69 = 3k ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{69}{3} = \frac{3k}{3} ~ & \textcolor{red}{ \text{ Divide both sides by 3.}} \\ 23 = k ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
4. Answer the Question. We’ve only found one side, but the question asks for the measure of all three sides. However, the remaining two sides can be found by substituting 23 for k into the expressions k + 1 and k + 2.
k + 1 = 23 + 1 and k + 2 = 23 + 2
= 24 = 25
Hence, the three sides measure 23 inches, 24 inches, and 25 inches.
5. Look Back. Does our solution make sense? Well, the three sides are certainly consecutive integers, and their sum is 23 inches + 24 inches + 25 inches = 72 inches, which was the given perimeter. Therefore, our solution is correct.
The three sides of a triangle are consecutive integers and the perimeter is 57 centimeters. Find the measure of each side of the triangle.
- Answer
-
18, 19, and 20 cm
Consecutive Odd Integers
The integer pair 19 and 21 are an example of a pair of consecutive odd integers. The important relation to notice is the fact that the second integer of this pair is two larger than its predecessor. That is, 21 = 19 + 2.
Let k represent an odd integer. The next consecutive odd integer is k + 2.
Thus, if k is an odd integer, then k + 2 is the next odd integer, k + 4 is the next odd integer after that, and so on.
The length and width of a rectangle are consecutive odd integers and the perimeter is 168 centimeters. Find the length and width of the rectangle.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. In this case, a carefully labeled diagram is the best way to indicate what the unknown variable represents.
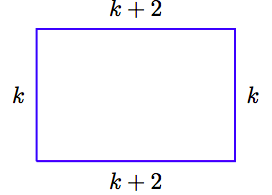
In our schematic diagram, if the width k is an odd integer, then the length k + 2 is the next consecutive odd integer.
2. Set up an Equation. To find the perimeter of the rectangle, sum the four sides.
\[P = k + (k + 2) + k + (k + 2)\nonumber \]
However, we’re given the fact that the perimeter is 168 centimeters. Thus,
\[168 = k + (k + 2) + k + (k + 2)\nonumber \]
3. Solve the Equation. On the right, regroup and combine like terms.
\[168 = 4k + 4\nonumber \]
Now, solve.
\[ \begin{aligned} 168 - 4 = 4k + 4 - 4 ~ & \textcolor{red}{ \text{ Subtract 4 from both sides.}} \\ 164 = 4k ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{164}{4} = \frac{4k}{4} ~ & \textcolor{red}{ \text{ Divide both sides by 4.}} \\ 41 = k ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
4. Answer the Question. We’ve only found the width, but the question asks for the measure of both the width and the length. However, the length can be found by substituting 41 for k into the expression k + 2.
k + 2 = 41 + 2
= 43
Hence, the width is 41 centimeters and the length is 43 centimeters.
5. Look Back. Does our solution make sense? Well, the width is 41 cm and the length is 43 cm, certainly consecutive odd integers. Further, the perimeter would be 41 cm + 43 cm + 41 cm + 43 cm = 168 cm, so our solution is correct.
The length and width of a rectangle are consecutive odd integers and the perimeter is 120 meters. Find the length and width of the rectangle.
- Answer
-
W = 29 cm, L = 31 cm
Tables
In the remaining applications in this section, we will strive to show how tables can be used to summarize information, define variables, and construct equations to help solve the application.
Hue inherits $10,000 and decides to invest in two different types of accounts, a savings account paying 2% interest, and a certificate of deposit paying 4% interest. He decides to invest $1,000 more in the certificate of deposit than in savings. Find the amount invested in each account.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We’re going to use a table to summarize information and declare variables. In the table that follows, we let S represent the amount Hue invests in the savings account. Using a variable letter that “sounds like” the quantity it represents is an excellent strategy. Thus, in this case, letting S represent the amount invested in savings is far better than letting x represent the amount invested in savings.
| Account Type | Amount Deposited |
|---|---|
| Savings Account (2%) | S |
| Certificate of Deposit (4%) | S + 1000 |
| Totals | 10000 |
Because S represents the investment in savings, and we’re told that the investment in the certificate of deposit (CD) is $1,000 more than the investment in savings, the investment in the CD is therefore S + 1000, as indicated in the table.
2. Set up an Equation. The second column of the table reveals that the sum of the individual investments in the CD and savings totals $10,000. Hence, the equation that models this application is
\[(S + 1000) + S = 10000.\nonumber \]
3. Solve the Equation. On the left, regroup and combine like terms.
\[2S + 1000 = 10000\nonumber \]
Now, solve.
\[ \begin{aligned} 2S + 1000 -1000 = 1000 - 1000 ~ & \textcolor{red}{ \text{ Subtract 1000 from both sides.}} \\ 2S = 9000 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{2S}{2} = \frac{9000}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ S = 4500 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
4. Answer the Question. We’ve only found the investment in savings, but the question also asks for the amount invested in the CD. However, the investment in the CD is easily found by substituting 4500 for S in the expression S + 1000.
S + 1000 = 4500 + 1000
= 5500.
Hence, the investment in savings is $4,500 and the investment in the CD is $5,500.
5. Look Back. Does our solution make sense? Well, the amount invested in the CD is $5,500, which is certainly $1,000 more than the $4,500 invested in savings. Secondly, the two investments total $5, 500 + $4, 500 = $10, 000, so our solution is correct.
Dylan invests a total of $2,750 in two accounts, a savings account paying 3% interest, and a mutual fund paying 5% interest. He invests $250 less in the mutual fund than in savings. Find the amount invested in each account.
- Answer
-
$1,500 in savings, $1,250 in the mutual fund
Jose cracks open his piggy bank and finds that he has $3.25 (325 cents), all in nickels and dimes. He has 10 more dimes than nickels. How many dimes and nickels does Jose have?
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We’re going to use a table to summarize information and declare variables. In the table that follows, we let N represent the number of nickels from the piggy bank. Using a variable letter that “sounds like” the quantity it represents is an excellent strategy. Thus, in this case, letting N represent the number of nickels is far better than letting x represent the number of nickels.
| Coins | Number of Coins | Value (cents) |
|---|---|---|
| Nickels (5 cents apiece) | N | 5N |
| Dimes (10 cents apiece) | N + 10 | 10(N + 10) |
| Totals | - | 325 |
Because there are 10 more dimes than nickels, the number of dimes is N + 10, recorded in the second column. In the third column, N nickels, worth 5 cents apiece, have a value of 5N cents. Next, N + 10 dimes, worth 10 cents apiece, have a value of 10(N + 10) cents. The final entry in the column gives the total value of the coins as 325 cents.
2. Set up an Equation. The third column of the table reveals that the sum of the coin values is 325 cents. Hence, the equation that models this application is
\[5N + 10(N + 10) = 325,\nonumber \]
which sums the value of the nickels and the value of the dimes to a total of 325 cents.
3. Solve the Equation. On the left, use the distributive property to remove parentheses.
\[5N + 10N + 100 = 325\nonumber \]
Combine like terms.
\[15N + 100 = 325\nonumber \]
Now, solve.
\[ \begin{aligned} 15N + 100 - 100 = 325 - 100 ~ & \textcolor{red}{ \text{ Subtract 100 from both sides.}} \\ 15N = 225 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{15N}{15} = \frac{225}{15} ~ & \textcolor{red}{ \text{ Divide both sides by 15.}} \\ N = 15 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
4. Answer the Question. We’ve only found the number of nickels, but the question also asks for the number of dimes. However, the number of dimes is easily found by substituting 15 for N in the expression N + 10.
N + 10 = 15 + 10
= 25.
Hence, Jose has 15 nickels and 25 dimes.
5. Look Back. Does our solution make sense? Well, the number of dimes is 25, which is certainly 10 more than 15 nickels. Also, the monetary value of 15 nickels is 75 cents and the monetary value of 25 dimes is 250 cents, a total of 325 cents, or $3.25, so our solution is correct.
David keeps his change in a bowl made by his granddaughter. There is $1.95 in change in the bowl, all in dimes and quarters. There are two fewer quarters than dimes. How many dimes and quarters does he have in the bowl?
- Answer
-
7 dimes, 5 quarters
A large children’s organization purchases tickets to the circus. The organization has a strict rule that every five children must be accompanied by one adult guardian. Hence, the organization orders five times as many child tickets as it does adult tickets. Child tickets are three dollars and adult tickets are six dollars. If the total cost of tickets is $4,200, how many child and adult tickets were purchased?
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We’re going to use a table to summarize information and declare variables. In the table that follows, we let A represent the number of adult tickets purchased. Using a variable letter that “sounds like” the quantity it represents is an excellent strategy. Thus, in this case, letting A represent the number of adult tickets is far better than letting x represent the number of adult tickets.
| Number of Tickets | Cost (dollars) | |
|---|---|---|
| Adults ($6 apiece) | A | 6A |
| Children ($3 apiece) | 5A | 3(5A) |
| Totals | - | 4200 |
Because there are 5 times as many children’s tickets purchased than adult tickets, the number of children’s tickets purchased is 5A, recorded in the second column. In the third column, 5A children’s tickets at $3 apiece will cost 3(5A) dollars, and A adult tickets at $6 apiece will cost 6A dollars. The final entry in the column gives the total cost of all tickets as $4,200.
2. Set up an Equation. The third column of the table reveals that the sum of the costs for both children and adult tickets is $4,200. Hence, the equation that models this application is
\[6A + 3(5A) = 4200\nonumber \]
which sums the cost of children and adult tickets at $4,200.
3. Solve the Equation. On the left, use the associative property to remove parentheses.
\[6A + 15A = 4200\nonumber \]
Combine like terms.
\[21A = 4200\nonumber \]
Now, solve.
\[ \begin{aligned} \frac{21A}{21} = \frac{4200}{21} ~ & \textcolor{red}{ \text{ Divide both sides by 21.}} \\ A = 200 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
4. Answer the Question. We’ve only found the number of adult tickets, but the question also asks for the number of children’s tickets. However, the number of children’s tickets is easily found by substituting 200 for A in the expression 5A.
5A = 5(200)
= 1000.
Hence, 1000 children’s tickets and 200 adult tickets were purchased.
5. Look Back. Does our solution make sense? Well, the number of children’s tickets purchased is 1000, which is certainly 5 times more than the 200 adult tickets purchased. Also, the monetary value of 1000 children’s tickets at $3 apiece is $3,000, and the monetary value of 200 adult tickets at $6 apiece is $1,200, a total cost of $4,200. Our solution is correct.
Emily purchase tickets to the IMAX theater for her family. An adult ticket cost $12 and a child ticket costs $4. She buys two more child tickets than adult tickets and the total cost is $136. How many adult and child tickets did she buy?
- Answer
-
8 adult and 10 child tickets
Exercises
1. The three sides of a triangle are consecutive odd integers. If the perimeter of the triangle is 39 inches, find the lengths of the sides of the triangle.
2. The three sides of a triangle are consecutive odd integers. If the perimeter of the triangle is 51 inches, find the lengths of the sides of the triangle.
3. The width and length of a rectangle are consecutive integers. If the perimeter of the rectangle is 142 inches, find the width and length of the rectangle.
4. The width and length of a rectangle are consecutive integers. If the perimeter of the rectangle is 166 inches, find the width and length of the rectangle.
5. The three sides of a triangle are consecutive even integers. If the perimeter of the triangle is 240 inches, find the lengths of the sides of the triangle.
6. The three sides of a triangle are consecutive even integers. If the perimeter of the triangle is 30 inches, find the lengths of the sides of the triangle.
7. The width and length of a rectangle are consecutive integers. If the perimeter of the rectangle is 374 inches, find the width and length of the rectangle.
8. The width and length of a rectangle are consecutive integers. If the perimeter of the rectangle is 318 inches, find the width and length of the rectangle.
9. The width and length of a rectangle are consecutive odd integers. If the perimeter of the rectangle is 208 inches, find the width and length of the rectangle.
10. The width and length of a rectangle are consecutive odd integers. If the perimeter of the rectangle is 152 inches, find the width and length of the rectangle.
11. The width and length of a rectangle are consecutive even integers. If the perimeter of the rectangle is 76 inches, find the width and length of the rectangle.
12. The width and length of a rectangle are consecutive even integers. If the perimeter of the rectangle is 300 inches, find the width and length of the rectangle.
13. The three sides of a triangle are consecutive even integers. If the perimeter of the triangle is 144 inches, find the lengths of the sides of the triangle.
14. The three sides of a triangle are consecutive even integers. If the perimeter of the triangle is 198 inches, find the lengths of the sides of the triangle.
15. The three sides of a triangle are consecutive integers. If the perimeter of the triangle is 228 inches, find the lengths of the sides of the triangle.
16. The three sides of a triangle are consecutive integers. If the perimeter of the triangle is 216 inches, find the lengths of the sides of the triangle.
17. The width and length of a rectangle are consecutive even integers. If the perimeter of the rectangle is 92 inches, find the width and length of the rectangle.
18. The width and length of a rectangle are consecutive even integers. If the perimeter of the rectangle is 228 inches, find the width and length of the rectangle.
19. The three sides of a triangle are consecutive integers. If the perimeter of the triangle is 105 inches, find the lengths of the sides of the triangle.
20. The three sides of a triangle are consecutive integers. If the perimeter of the triangle is 123 inches, find the lengths of the sides of the triangle.
21. The width and length of a rectangle are consecutive odd integers. If the perimeter of the rectangle is 288 inches, find the width and length of the rectangle.
22. The width and length of a rectangle are consecutive odd integers. If the perimeter of the rectangle is 352 inches, find the width and length of the rectangle.
23. The three sides of a triangle are consecutive odd integers. If the perimeter of the triangle is 165 inches, find the lengths of the sides of the triangle.
24. The three sides of a triangle are consecutive odd integers. If the perimeter of the triangle is 99 inches, find the lengths of the sides of the triangle.
25. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 8 children must be accompanied by one adult guardian. Hence, the organization orders 8 times as many child tickets as it does adult tickets. Child tickets are $7 and adult tickets are $19. If the total cost of tickets is $975, how many adult tickets were purchased?
26. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 2 children must be accompanied by one adult guardian. Hence, the organization orders 2 times as many child tickets as it does adult tickets. Child tickets are $6 and adult tickets are $16. If the total cost of tickets is $532, how many adult tickets were purchased?
27. Judah cracks open a piggy bank and finds $3.30 (330 cents), all in nickels and dimes. There are 15 more dimes than nickels. How many nickels does Judah have?
28. Texas cracks open a piggy bank and finds $4.90 (490 cents), all in nickels and dimes. There are 13 more dimes than nickels. How many nickels does Texas have?
29. Steve cracks open a piggy bank and finds $4.00 (400 cents), all in nickels and dimes. There are 7 more dimes than nickels. How many nickels does Steve have?
30. Liz cracks open a piggy bank and finds $4.50 (450 cents), all in nickels and dimes. There are 15 more dimes than nickels. How many nickels does Liz have?
31. Jason inherits $20,300 and decides to invest in two different types of accounts, a savings account paying 2.5% interest, and a certificate of deposit paying 5% interest. He decides to invest $7,300 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
32. Trinity inherits $24,300 and decides to invest in two different types of accounts, a savings account paying 2% interest, and a certificate of deposit paying 5.75% interest. She decides to invest $8,500 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
33. Gina cracks open a piggy bank and finds $4.50 (450 cents), all in nickels and dimes. There are 15 more dimes than nickels. How many nickels does Gina have?
34. Dylan cracks open a piggy bank and finds $4.05 (405 cents), all in nickels and dimes. There are 6 more dimes than nickels. How many nickels does Dylan have?
35. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 2 children must be accompanied by one adult guardian. Hence, the organization orders 2 times as many child tickets as it does adult tickets. Child tickets are $4 and adult tickets are $10. If the total cost of tickets is $216, how many adult tickets were purchased?
36. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 2 children must be accompanied by one adult guardian. Hence, the organization orders 2 times as many child tickets as it does adult tickets. Child tickets are $7 and adult tickets are $11. If the total cost of tickets is $375, how many adult tickets were purchased?
37. Connie cracks open a piggy bank and finds $3.70 (370 cents), all in nickels and dimes. There are 7 more dimes than nickels. How many nickels does Connie have?
38. Don cracks open a piggy bank and finds $3.15 (315 cents), all in nickels and dimes. There are 3 more dimes than nickels. How many nickels does Don have?
39. Mary inherits $22,300 and decides to invest in two different types of accounts, a savings account paying 2% interest, and a certificate of deposit paying 4% interest. She decides to invest $7,300 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
40. Amber inherits $26,000 and decides to invest in two different types of accounts, a savings account paying 2.25% interest, and a certificate of deposit paying 4.25% interest. She decides to invest $6,200 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
41. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 8 children must be accompanied by one adult guardian. Hence, the organization orders 8 times as many child tickets as it does adult tickets. Child tickets are $6 and adult tickets are $16. If the total cost of tickets is $1024, how many adult tickets were purchased?
42. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 3 children must be accompanied by one adult guardian. Hence, the organization orders 3 times as many child tickets as it does adult tickets. Child tickets are $3 and adult tickets are $18. If the total cost of tickets is $351, how many adult tickets were purchased?
43. Alan inherits $25,600 and decides to invest in two different types of accounts, a savings account paying 3.5% interest, and a certificate of deposit paying 6% interest. He decides to invest $6,400 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
44. Mercy inherits $27,100 and decides to invest in two different types of accounts, a savings account paying 3% interest, and a certificate of deposit paying 4% interest. She decides to invest $8,700 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
45. Tony inherits $20,600 and decides to invest in two different types of accounts, a savings account paying 2% interest, and a certificate of deposit paying 4% interest. He decides to invest $9,200 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
46. Connie inherits $17,100 and decides to invest in two different types of accounts, a savings account paying 2% interest, and a certificate of deposit paying 5.5% interest. She decides to invest $6,100 more in the certificate of deposit than in savings. Find the amount invested in the savings account.
47. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 2 children must be accompanied by one adult guardian. Hence, the organization orders 2 times as many child tickets as it does adult tickets. Child tickets are $2 and adult tickets are $14. If the total cost of tickets is $234, how many adult tickets were purchased?
48. A large children’s organization purchases tickets to the circus. The organization has a strict rule that every 8 children must be accompanied by one adult guardian. Hence, the organization orders 8 times as many child tickets as it does adult tickets. Child tickets are $8 and adult tickets are $13. If the total cost of tickets is $1078, how many adult tickets were purchased?
Answers
1. 11 in., 13 in., 15 in.
3. 35 in., 36 in.
5. 78 in., 80 in., 82 in.
7. 93 in., 94 in.
9. 51 in., 53 in.
11. 18 in., 20 in.
13. 46 in., 48 in., 50 in.
15. 75 in., 76 in., 77 in.
17. 22 in., 24 in.
19. 34 in., 35 in., 36 in.
21. 71 in., 73 in.
23. 53 in., 55 in., 57 in.
25. 13 adult tickets
27. 12 nickels
29. 22 nickels
31. $6, 500
33. 20 nickels
35. 12 child tickets
37. 20 nickels
39. $7, 500
41. 16 child tickets
43. $9, 600
45. $5, 700
47. 13 child tickets


