9.8: Solve Geometry Applications- Circles and Irregular Figures
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Use the properties of circles
- Find the area of irregular figures
Before you get started, take this readiness quiz.
- Evaluate x2 when x = 5. If you missed this problem, review Example 2.3.3.
- Using 3.14 for π, approximate the (a) circumference and (b) the area of a circle with radius 8 inches. If you missed this problem, review Example 5.6.12.
- Simplify 227(0.25)2 and round to the nearest thousandth. If you missed this problem, review Example 5.5.9.
In this section, we’ll continue working with geometry applications. We will add several new formulas to our collection of formulas. To help you as you do the examples and exercises in this section, we will show the Problem Solving Strategy for Geometry Applications here.
Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.
Step 3. Name what you are looking for. Choose a variable to represent that quantity
Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
Use the Properties of Circles
Do you remember the properties of circles from Decimals and Fractions? We’ll show them here again to refer to as we use them to solve applications.
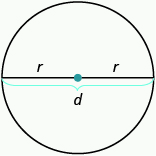
- r is the length of the radius
- d is the length of the diameter
- d = 2r
- Circumference is the perimeter of a circle. The formula for circumference is C = 2πr
- The formula for area of a circle is A = πr2
Remember, that we approximate π with 3.14 or 227 depending on whether the radius of the circle is given as a decimal or a fraction. If you use the π key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the π key uses more than two decimal places.
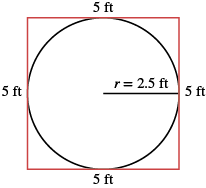
A circular sandbox has a radius of 2.5 feet. Find the (a) circumference and (b) area of the sandbox.
Solution
(a)
| Step 1. Read the problem. Draw the figure and label it with the given information. | 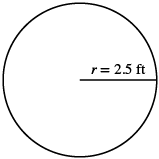 |
| Step 2. Identify what you are looking for. | the circumference of the circle |
| Step 3. Name. Choose a variable to represent it. | Let c = circumference of the circle |
| Step 4. Translate. Write the appropriate formula. Substitute. | C=2πrC=2π(2.5) |
| Step 5. Solve the equation. | C≈2(3.14)(2.5)C≈15ft |
| Step 6. Check. Does this answer make sense? |
Yes. If we draw a square around the circle, its sides would be 5 ft (twice the radius), so its perimeter would be 20 ft. This is slightly more than the circle's circumference, 15.7 ft.
|
| Step 7. Answer the question. | The circumference of the sandbox is 15.7 feet. |
(b)
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | the area of the circle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area of the circle |
| Step 4. Translate. Write the appropriate formula. Substitute. | A=πr2A=π(2.5)2 |
| Step 5. Solve the equation. | A≈(3.14)(2.5)2A≈19.625sq.ft |
| Step 6. Check. Does this answer make sense? | Yes. If we draw a square around the circle, its sides would be 5 ft, as shown in part (a). So the area of the square would be 25 sq. ft. This is slightly more than the circle's area, 19.625 sq. ft. |
| Step 7. Answer the question. | The area of the circle is 19.625 square feet. |
A circular mirror has radius of 5 inches. Find the (a) circumference and (b) area of the mirror.
- Answer a
-
31.4 in.
- Answer b
-
78.5 sq. in.
A circular spa has radius of 4.5 feet. Find the (a) circumference and (b) area of the spa.
- Answer a
-
28.26 ft
- Answer b
-
63.585 sq. ft
We usually see the formula for circumference in terms of the radius r of the circle:
C=2πr
But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms of d.
C=2πrUsingthecommutativeproperty,wegetC=π⋅2rThensubstitutingd=2rC=π⋅dSoC=πd
We will use this form of the circumference when we’re given the length of the diameter instead of the radius.
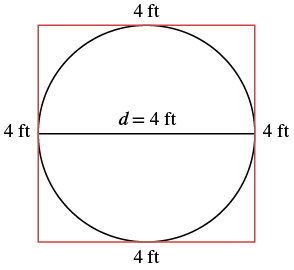
A circular table has a diameter of four feet. What is the circumference of the table?
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 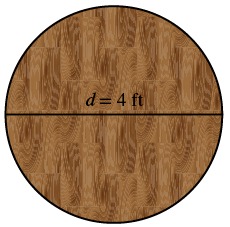 |
| Step 2. Identify what you are looking for. | the circumference of the table |
| Step 3. Name. Choose a variable to represent it. | Let c = the circumference of the table |
| Step 4. Translate. Write the appropriate formula for the situation. Substitute. | C=πdC=π(4) |
| Step 5. Solve the equation, using 3.14 for π. | C≈(3.14)(4)C≈12.56ft |
| Step 6. Check. |
If we put a square around the circle, its side would be 4. The perimeter would be 16. It makes sense that the circumference of the circle, 12.56, is a little less than 16.
|
| Step 7. Answer the question. | The diameter of the table is 12.56 square feet. |
Find the circumference of a circular fire pit whose diameter is 5.5 feet.
- Answer
-
17.27 ft
If the diameter of a circular trampoline is 12 feet, what is its circumference?
- Answer
-
37.68 ft.
Find the diameter of a circle with a circumference of 47.1 centimeters.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 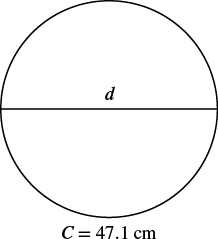 |
| Step 2. Identify what you are looking for. | the diameter of the circle |
| Step 3. Name. Choose a variable to represent it. | Let d = the diameter of the circle |
| Step 4. Translate. Write the formula. Substitute, using 3.14 to approximate π. | C=πd47.1≈3.14d |
| Step 5. Solve. | 47.113.14≈3.14d3.1415≈d |
| Step 6. Check. | 47.1?=(3.14)(15)47.1=47.1✓ |
| Step 7. Answer the question. | The diameter of the circle is approximately 15 centimeters. |
Find the diameter of a circle with circumference of 94.2 centimeters.
- Answer
-
30 cm
Find the diameter of a circle with circumference of 345.4 feet.
- Answer
-
110 ft
Find the Area of Irregular Figures
So far, we have found area for rectangles, triangles, trapezoids, and circles. An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or more standard geometric shapes. To find the area of one of these irregular figures, we can split it into figures whose formulas we know and then add the areas of the figures.
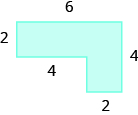
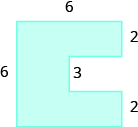
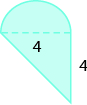
Find the area of the shaded region.
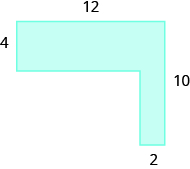
Solution
The given figure is irregular, but we can break it into two rectangles. The area of the shaded region will be the sum of the areas of both rectangles.
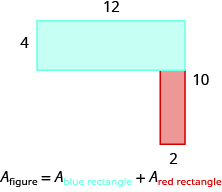
The blue rectangle has a width of 12 and a length of 4. The red rectangle has a width of 2, but its length is not labeled. The right side of the figure is the length of the red rectangle plus the length of the blue rectangle. Since the right side of the blue rectangle is 4 units long, the length of the red rectangle must be 6 units.
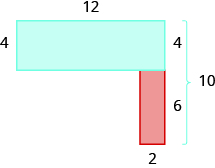
Afigure=Arectangle+ArectangleAfigure=bh+bhAfigure=12⋅4+2⋅6Afigure=48+12Afigure=60
The area of the figure is 60 square units.
Is there another way to split this figure into two rectangles? Try it, and make sure you get the same area.
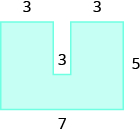
Find the area of each shaded region:
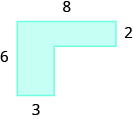
- Answer
-
28 sq. units
Find the area of each shaded region:
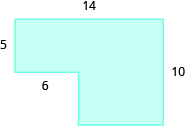
- Answer
-
110 sq. units
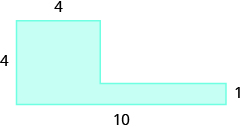
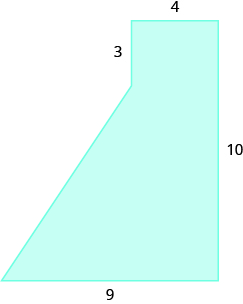
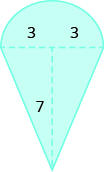
Find the area of the shaded region.
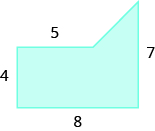
Solution
We can break this irregular figure into a triangle and rectangle. The area of the figure will be the sum of the areas of triangle and rectangle.
The rectangle has a length of 8 units and a width of 4 units.
We need to find the base and height of the triangle.
Since both sides of the rectangle are 4, the vertical side of the triangle is 3, which is 7 − 4. The length of the rectangle is 8, so the base of the triangle will be 3, which is 8 − 4.
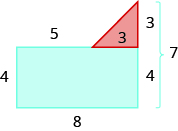
Now we can add the areas to find the area of the irregular figure.
Afigure=Arectangle+AtriangleAfigure=lw+12bhAfigure=8⋅4+12⋅3⋅3Afigure=32+4.5Afigure=3.65sq.units
The area of the figure is 36.5 square units.
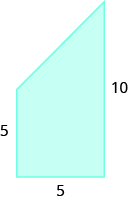
Find the area of each shaded region.

- Answer
-
36.5 sq. units
Find the area of each shaded region.
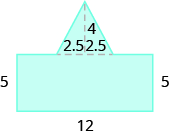
- Answer
-
70 sq. units
A high school track is shaped like a rectangle with a semi-circle (half a circle) on each end. The rectangle has length 105 meters and width 68 meters. Find the area enclosed by the track. Round your answer to the nearest hundredth.

Solution
We will break the figure into a rectangle and two semi-circles. The area of the figure will be the sum of the areas of the rectangle and the semicircles.

The rectangle has a length of 105 m and a width of 68 m. The semi-circles have a diameter of 68 m, so each has a radius of 34 m.
Afigure=Arectangle+AsemicirclesAfigure=bh+2(12π⋅r2)Afigure≈105⋅68+2(12⋅3.14⋅342)Afigure≈7140+3629.84Afigure≈10,769.84squaremeters
Find the area:
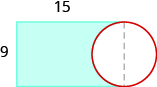
- Answer
-
103.2 sq. units
Find the area:
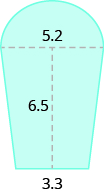
- Answer
-
38.24 sq. units
Circumference of a Circle
Area of a Circle
Area of an L-shaped polygon
Area of an L-shaped polygon with Decimals
Perimeter Involving a Rectangle and Circle
Area Involving a Rectangle and Circle
Practice Makes Perfect
Use the Properties of Circles
In the following exercises, solve using the properties of circles.
- The lid of a paint bucket is a circle with radius 7 inches. Find the (a) circumference and (b) area of the lid.
- An extra-large pizza is a circle with radius 8 inches. Find the (a) circumference and (b) area of the pizza.
- A farm sprinkler spreads water in a circle with radius of 8.5 feet. Find the (a) circumference and (b) area of the watered circle.
- A circular rug has radius of 3.5 feet. Find the (a) circumference and (b) area of the rug.
- A reflecting pool is in the shape of a circle with diameter of 20 feet. What is the circumference of the pool?
- A turntable is a circle with diameter of 10 inches. What is the circumference of the turntable?
- A circular saw has a diameter of 12 inches. What is the circumference of the saw?
- A round coin has a diameter of 3 centimeters. What is the circumference of the coin?
- A barbecue grill is a circle with a diameter of 2.2 feet. What is the circumference of the grill?
- The top of a pie tin is a circle with a diameter of 9.5 inches. What is the circumference of the top?
- A circle has a circumference of 163.28 inches. Find the diameter.
- A circle has a circumference of 59.66 feet. Find the diameter.
- A circle has a circumference of 17.27 meters. Find the diameter.
- A circle has a circumference of 80.07 centimeters. Find the diameter.
In the following exercises, find the radius of the circle with given circumference.
- A circle has a circumference of 150.72 feet.
- A circle has a circumference of 251.2 centimeters.
- A circle has a circumference of 40.82 miles.
- A circle has a circumference of 78.5 inches.
Find the Area of Irregular Figures
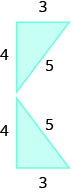
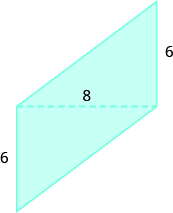
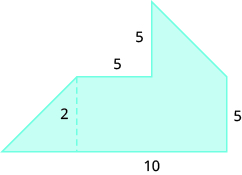
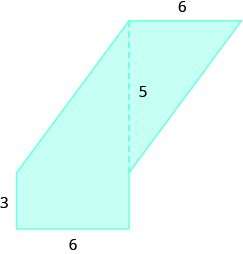
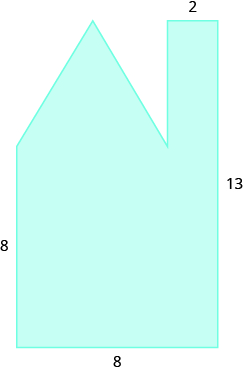
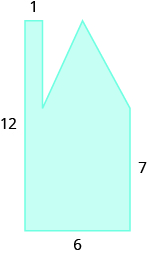
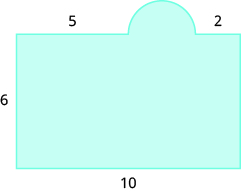
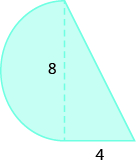
In the following exercises, find the area of the irregular figure. Round your answers to the nearest hundredth.
In the following exercises, solve.
- A city park covers one block plus parts of four more blocks, as shown. The block is a square with sides 250 feet long, and the triangles are isosceles right triangles. Find the area of the park.

- A gift box will be made from a rectangular piece of cardboard measuring 12 inches by 20 inches, with squares cut out of the corners of the sides, as shown. The sides of the squares are 3 inches. Find the area of the cardboard after the corners are cut out.

- Perry needs to put in a new lawn. His lot is a rectangle with a length of 120 feet and a width of 100 feet. The house is rectangular and measures 50 feet by 40 feet. His driveway is rectangular and measures 20 feet by 30 feet, as shown. Find the area of Perry’s lawn.

- Denise is planning to put a deck in her back yard. The deck will be a 20-ft by 12-ft rectangle with a semicircle of diameter 6 feet, as shown below. Find the area of the deck.
Everyday Math
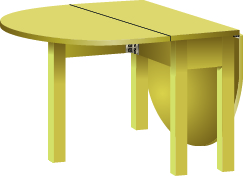
- Area of a Tabletop Yuki bought a drop-leaf kitchen table. The rectangular part of the table is a 1-ft by 3-ft rectangle with a semicircle at each end, as shown.(a) Find the area of the table with one leaf up. (b) Find the area of the table with both leaves up.
- Painting Leora wants to paint the nursery in her house. The nursery is an 8-ft by 10-ft rectangle, and the ceiling is 8 feet tall. There is a 3-ft by 6.5-ft door on one wall, a 3-ft by 6.5-ft closet door on another wall, and one 4-ft by 3.5-ft window on the third wall. The fourth wall has no doors or windows. If she will only paint the four walls, and not the ceiling or doors, how many square feet will she need to paint?
Writing Exercises
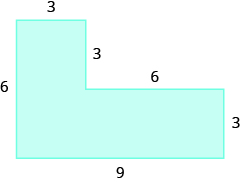
- Describe two different ways to find the area of this figure, and then show your work to make sure both ways give the same area.
- A circle has a diameter of 14 feet. Find the area of the circle (a) using 3.14 for π (b) using 227 for π. (c) Which calculation to do prefer? Why?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

(b) After looking at the checklist, do you think you are well prepared for the next section? Why or why not?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."