Home
Bookshelves
Pre-Algebra
Prealgebra 1e (OpenStax)
9: Math Models and Geometry
9.9: Solve Geometry Applications- Volume and Surface Area (Part 1)

9.9: Solve Geometry Applications- Volume and Surface Area (Part 1)

Last updated
Save as PDF

Page ID: 5010

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Find volume and surface area of rectangular solids
Find volume and surface area of spheres
Find volume and surface area of cylinders
Find volume of cones

be prepared!

Before you get started, take this readiness quiz.

Evaluate x³ when x = 5. If you missed this problem, review Example 2.3.3.
Evaluate 2^x when x = 5. If you missed this problem, review Example 2.3.4.
Find the area of a circle with radius $\dfrac{7}{2}$. If you missed this problem, review Example 5.6.12.

In this section, we will finish our study of geometry applications. We find the volume and surface area of some three-dimensional figures. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.

Problem Solving Strategy for Geometry Applications

Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.
Step 3. Name what you are looking for. Choose a variable to represent that quantity.
Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.

Find Volume and Surface Area of Rectangular Solids

A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See Figure $\PageIndex{1}$). The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.

$This is an image of a wooden crate.$

Figure $\PageIndex{1}$ - This wooden crate is in the shape of a rectangular solid.

Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown in Figure $\PageIndex{2}$ has length 4 units, width 2 units, and height 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.

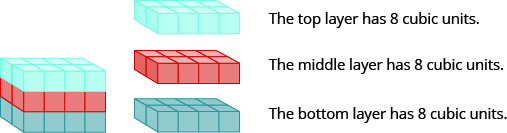
$A rectangular solid is shown. Each layer is composed of 8 cubes, measuring 2 by 4. The top layer is pink. The middle layer is orange. The bottom layer is green. Beside this is an image of the top layer that says “The top layer has 8 cubic units.” The orange layer is shown and says “The middle layer has 8 cubic units.” The green layer is shown and says, “The bottom layer has 8 cubic units.”$

Figure $\PageIndex{2}$ - Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 4 by 2 by 3 rectangular solid has 24 cubic units.

Altogether there are 24 cubic units. Notice that 24 is the length × width × height.

$The top line says V equals L times W times H. Beneath the V is 24, beneath the equal sign is another equal sign, beneath the L is a 4, beneath the W is a 2, beneath the H is a 3.$

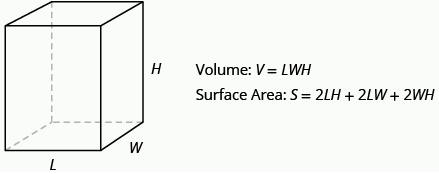
The volume, V, of any rectangular solid is the product of the length, width, and height.

\[V= LWH\]

We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B, is equal to length × width.

\[B = L \cdot W\]

We can substitute B for L • W in the volume formula to get another form of the volume formula.

\[\begin{split} V &= \textcolor{red}{L \cdot W} \cdot H \\ V &= \textcolor{red}{(L \cdot W)} \cdot H \\ V &= \textcolor{red}{B} h \end{split}\]

We now have another version of the volume formula for rectangular solids. Let’s see how this works with the 4 × 2 × 3 rectangular solid we started with. See Figure $\PageIndex{3}$.

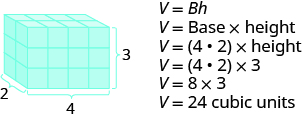
$An image of a rectangular solid is shown. It is made up of cubes. It is labeled as 2 by 4 by 3. Beside the solid is V equals Bh. Below this is V equals Base times height. Below Base is parentheses 4 times 2. The next line says V equals parentheses 4 times 2 times 3. Below that is V equals 8 times 3, then V equals 24 cubic units.$

Figure $\PageIndex{3}$

To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.

\[\begin{split} A_{front} &= L \times W \qquad A_{side} = L \times W \qquad A_{top} = L \times W \\ A_{front} &= 4 \cdot 3 \qquad \quad \; A_{side} = 2 \cdot 3 \qquad \quad \; A_{top} = 4 \cdot 2 \\ A_{front} &= 12 \qquad \qquad A_{side} = 6 \qquad \qquad \; \; A_{top} = 8 \end{split}\]

Notice for each of the three faces you see, there is an identical opposite face that does not show.

\[\begin{split} S &= (front + back)+(left\; side + right\; side) + (top + bottom) \\ S &= (2 \cdot front) + (2 \cdot left\; side) + (2 \cdot top) \\ S &= 2 \cdot 12 + 2 \cdot 6 + 2 \cdot 8 \\ S &= 24 + 12 + 16 \\ S &= 52\; sq.\; units \end{split}\]

The surface area S of the rectangular solid shown in Figure $\PageIndex{3}$ is 52 square units.

In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure $\PageIndex{4}$). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side.

\[S = 2LH + 2LW + 2WH\]

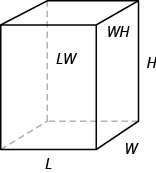
$A rectangular solid is shown. The sides are labeled L, W, and H. One face is labeled LW and another is labeled WH.$

Figure $\PageIndex{4}$ - For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.

Definition: Volume and Surface Area of a Rectangular Solid

For a rectangular solid with length L, width W, and height H:

$A rectangular solid is shown. The sides are labeled L, W, and H. Beside it is Volume: V equals LWH equals BH. Below that is Surface Area: S equals 2LH plus 2LW plus 2WH.$

Example $\PageIndex{1}$:

For a rectangular solid with length 14 cm, height 17 cm, and width 9 cm, find the (a) volume and (b) surface area.

Solution

Step 1 is the same for both (a) and (b), so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.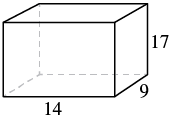

$CNX_BMath_Figure_09_06_038_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the rectangular solid
Step 3. Name. Choose a variable to represent it.	Let V = volume
Step 4. Translate. Write the appropriate formula. Substitute.	$$\begin{split} V &= LWH \\ V &= 14 \cdot 9 \cdot 9 \cdot 17 \end{split}$$
Step 5. Solve the equation.	$$V = 2,142$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is 2,142 cubic centimeters.

(b)

Step 2. Identify what you are looking for.	the surface area of the solid
Step 3. Name. Choose a variable to represent it.	Let S = surface area
Step 4. Translate. Write the appropriate formula. Substitute.	$$\begin{split} S &= 2LH + 2LW + 2WH \\ S &= 2(14 \cdot 17) + 2(14 \cdot 9) + 2(9 \cdot 17) \end{split}$$
Step 5. Solve the equation.	$$S = 1,034$$
Step 6. Check.	Double-check with a calculator.
Step 7. Answer the question.	The surface area is 1,034 square centimeters.

Exercise $\PageIndex{1}$:

Find the (a) volume and (b) surface area of rectangular solid with the: length 8 feet, width 9 feet, and height 11 feet.

Answer a: 792 cu. ft

Answer b: 518 sq. ft

Exercise $\PageIndex{2}$:

Find the (a) volume and (b) surface area of rectangular solid with the: length 15 feet, width 12 feet, and height 8 feet.

Answer a: 1,440 cu. ft

Answer b: 792 sq. ft

Example $\PageIndex{2}$:

A rectangular crate has a length of 30 inches, width of 25 inches, and height of 20 inches. Find its (a) volume and (b) surface area.

Solution

Step 1 is the same for both (a) and (b), so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.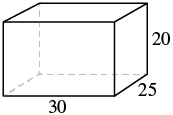

$CNX_BMath_Figure_09_06_039_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the crate
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute.	$$\begin{split} V &= LWH \\ V &= 30 \cdot 25 \cdot 20 \end{split}$$
Step 5. Solve the equation.	$$V = 15,000$$
Step 6. Check.	Double check your math.
Step 7. Answer the question.	The volume is 15,000 cubic inches.

(b)

Step 2. Identify what you are looking for.	the surface area of the crate
Step 3. Name. Choose a variable to represent it.	the surface area of the crate
Step 4. Translate. Write the appropriate formula. Substitute.	$$\begin{split} S &= 2LH + 2LW + 2WH \\ S &= 2(30 \cdot 20) + 2(30 \cdot 25) + 2(25 \cdot 20) \end{split}$$
Step 5. Solve the equation.	$$S = 3,700$$
Step 6. Check.	Check it yourself!
Step 7. Answer the question.	The surface area is 3,700 square inches.

Exercise $\PageIndex{3}$:

A rectangular box has length 9 feet, width 4 feet, and height 6 feet. Find its (a) volume and (b) surface area.

Answer a: 216 cu. ft

Answer b: 228 sq. ft

Exercise $\PageIndex{4}$:

A rectangular suitcase has length 22 inches, width 14 inches, and height 9 inches. Find its (a) volume and (b) surface area.

Answer a: 2,772 cu. in

Answer b: 1,264 sq. in.

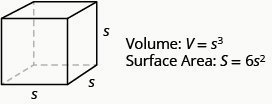
Volume and Surface Area of a Cube

A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:

\[\begin{split} V &= LWH \quad \; S = 2LH + 2LW + 2WH \\ V &= s \cdot s \cdot s \quad S = 2s \cdot s + 2s \cdot s + 2s \cdot s \\ V &= s^{3} \qquad \quad S = 2s^{2} + 2s^{2} + 2s^{2} \\ &\qquad \qquad \quad \; S = 6s^{2} \end{split}\]

So for a cube, the formulas for volume and surface area are V = s³ and S = 6s².

Definition: Volume and Surface Area of a Cube

For any cube with sides of length s,

$An image of a cube is shown. Each side is labeled s. Beside this is Volume: V equals s cubed. Below that is Surface Area: S equals 6 times s squared.$

Example $\PageIndex{3}$:

A cube is 2.5 inches on each side. Find its (a) volume and (b) surface area.

Solution

Step 1 is the same for both (a) and (b), so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.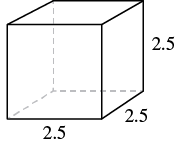

$CNX_BMath_Figure_09_06_040_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the crate
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula.	$$V = s^{3}$$
Step 5. Solve. Substitute and solve.	$$\begin{split} V &= (2.5)^{3} \\ V &= 15.625 \end{split}$$
Step 6. Check.	Check your work.
Step 7. Answer the question.	The volume is 15.625 cubic inches.

(b)

Step 2. Identify what you are looking for.	the surface area of the crate
Step 3. Name. Choose a variable to represent it.	the surface area of the crate
Step 4. Translate. Write the appropriate formula.	$$S = 6s^{2}$$
Step 5. Solve. Substitute and solve.	$$\begin{split} S &= 6 \cdot (2.5)^{2} \\ S &= 37.5 \end{split}$$
Step 6. Check.	The check is left to you.
Step 7. Answer the question.	The surface area is 37.5 square inches.

Exercise $\PageIndex{5}$:

For a cube with side 4.5 meters, find the (a) volume and (b) surface area of the cube.

Answer a: 91.125 cu. m

Answer b: 121.5 sq. m

Exercise $\PageIndex{6}$:

For a cube with side 7.3 yards, find the (a) volume and (b) surface area of the cube.

Answer a: 389.017 cu. yd.

Answer b: 319.74 sq. yd.

Example $\PageIndex{4}$:

A notepad cube measures 2 inches on each side. Find its (a) volume and (b) surface area.

Solution

Step 1. Read the problem. Draw the figure and label it with the given information.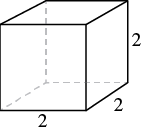

$CNX_BMath_Figure_09_06_041_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the crate
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula.	$$V = s^{3}$$
Step 5. Solve the equation.	$$\begin{split} V &= 2^{3} \\ V &= 8 \end{split}$$
Step 6. Check.	Check that you did the calculations correctly.
Step 7. Answer the question.	The volume is 8 cubic inches

(b)

Step 2. Identify what you are looking for.	the surface area of the crate
Step 3. Name. Choose a variable to represent it.	the surface area of the crate
Step 4. Translate. Write the appropriate formula.	$$S = 6s^{2}$$
Step 5. Solve the equation.	$$\begin{split} S &= 6 \cdot 2^{2} \\ S &= 24 \end{split}$$
Step 6. Check.	The check is left to you.
Step 7. Answer the question.	The surface area is 24 square inches.

Exercise $\PageIndex{7}$:

A packing box is a cube measuring 4 feet on each side. Find its (a) volume and (b) surface area.

Answer a: 64 cu. ft

Answer b: 96 sq. ft

Exercise $\PageIndex{8}$:

A wall is made up of cube-shaped bricks. Each cube is 16 inches on each side. Find the (a) volume and (b) surface area of each cube.

Answer a: 4,096 cu. in.

Answer b: 1,536

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Volume and Surface Area of a Rectangular Solid

Example \(\PageIndex{1}\):

Exercise \(\PageIndex{1}\):

Exercise \(\PageIndex{2}\):

Example \(\PageIndex{2}\):

Exercise \(\PageIndex{3}\):

Exercise \(\PageIndex{4}\):

Definition: Volume and Surface Area of a Cube

Example \(\PageIndex{3}\):

Exercise \(\PageIndex{5}\):

Exercise \(\PageIndex{6}\):

Example \(\PageIndex{4}\):

Exercise \(\PageIndex{7}\):

Exercise \(\PageIndex{8}\):