9.4: Use Properties of Angles, Triangles, and the Pythagorean Theorem (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Use the properties of angles
- Use the properties of triangles
- Use the Pythagorean Theorem
Before you get started, take this readiness quiz.
- Solve: x + 3 + 6 = 11. If you missed this problem, review Example 8.1.6.
- Solve: a45=43. If you missed this problem, review Example 6.5.3.
- Simplify: √36+64. If you missed this problem, review Example 5.12.4.
So far in this chapter, we have focused on solving word problems, which are similar to many real-world applications of algebra. In the next few sections, we will apply our problem-solving strategies to some common geometry problems.
Use the Properties of Angles
Are you familiar with the phrase ‘do a 180’? It means to turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is 180 degrees. See Figure 9.4.1.
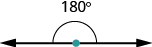
Figure 9.4.1
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex. An angle is named by its vertex. In Figure 9.4.2, ∠A is the angle with vertex at point A. The measure of ∠A is written m ∠ A.
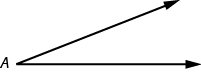
Figure 9.4.2 - ∠ A is the angle with vertex at point A.
We measure angles in degrees, and use the symbol ° to represent degrees. We use the abbreviation m for the measure of an angle. So if ∠A is 27°, we would write m ∠ A = 27.
If the sum of the measures of two angles is 180°, then they are called supplementary angles. In Figure 9.4.3, each pair of angles is supplementary because their measures add to 180°. Each angle is the supplement of the other.
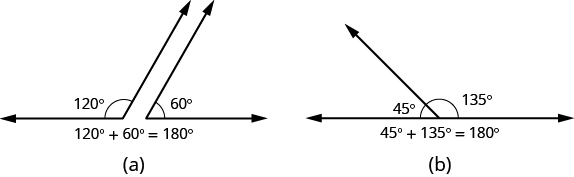
Figure 9.4.3 - The sum of the measures of supplementary angles is 180°.
If the sum of the measures of two angles is 90°, then the angles are complementary angles. In Figure 9.4.4, each pair of angles is complementary, because their measures add to 90°. Each angle is the complement of the other.
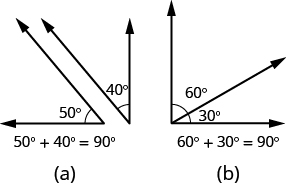
Figure 9.4.4 - The sum of the measures of complementary angles is 90°.
If the sum of the measures of two angles is 180°, then the angles are supplementary.
If ∠A and ∠B are supplementary, then m∠A + m∠B = 180°.
If the sum of the measures of two angles is 90°, then the angles are complementary.
If ∠A and ∠B are complementary, then m∠A + m∠B = 90°.
In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.
Step 1. Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.
Step 2. Identify what you are looking for
Step 3. Name what you are looking for and choose a variable to represent it.
Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.
An angle measures 40°. Find (a) its supplement, and (b) its complement.
Solution
(a)
| Step 1. Read the problem. Draw the figure and label it with the given information. | 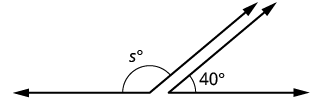 |
| Step 2. Identify what you are looking for. | the supplement of a 40° |
| Step 3. Name. Choose a variable to represent it. | let s = the measure of the supplement |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B=180 |
| Step 5. Solve the equation. | s+40=180s=140 |
| Step 6. Check. | 140+40?=180180=180✓ |
| Step 7. Answer the question. | The supplement of the 40° angle is 140°. |
(b)
| Step 1. Read the problem. Draw the figure and label it with the given information. | 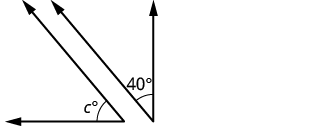 |
| Step 2. Identify what you are looking for. | the complement of a 40° |
| Step 3. Name. Choose a variable to represent it. | let c = the measure of the complement |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B=90 |
| Step 5. Solve the equation. | c+40=90c=50 |
| Step 6. Check. | 50+40?=9090=90✓ |
| Step 7. Answer the question. | The supplement of the 40° angle is 50°. |
An angle measures 25°. Find (a) its supplement, and (b) its complement.
- Answer a
-
155°
- Answer b
-
65°
An angle measures 77°. Find (a) its supplement, and (b) its complement.
- Answer a
-
103°
- Answer b
-
13°
Did you notice that the words complementary and supplementary are in alphabetical order just like 90 and 180 are in numerical order?
Two angles are supplementary. The larger angle is 30° more than the smaller angle. Find the measure of both angles.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 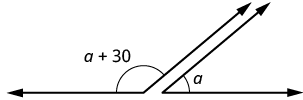 |
| Step 2. Identify what you are looking for. | the measures of both angles |
| Step 3. Name. Choose a variable to represent it. |
let a = measure of the smaller angle a + 30 = measure of larger angle |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B=180 |
| Step 5. Solve the equation. | (a+30)+a=1802a+30=1802a=150a=75measureofsmalleranglea+30measureoflargerangle75+30105 |
| Step 6. Check. | m∠A+m∠B=18075+105?=180180=180✓ |
| Step 7. Answer the question. | The measures of the angles are 75° and 105°. |
Two angles are supplementary. The larger angle is 100° more than the smaller angle. Find the measures of both angles.
- Answer
-
40°, 140°
Two angles are complementary. The larger angle is 40° more than the smaller angle. Find the measures of both angles.
- Answer
-
25°, 65°
Use the Properties of Triangles
What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle in Figure 9.4.5 is called ΔABC, read ‘triangle ABC’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.
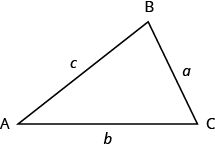
Figure 9.4.5 - ΔABC has vertices A, B, and C and sides a, b, and c.
The three angles of a triangle are related in a special way. The sum of their measures is 180°.
m∠A+m∠B+m∠C=180°
For any ΔABC, the sum of the measures of the angles is 180°.
m∠A+m∠B+m∠C=180°
The measures of two angles of a triangle are 55° and 82°. Find the measure of the third angle.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 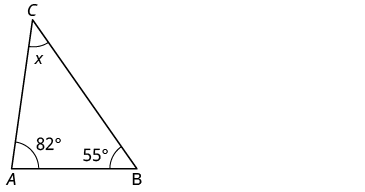 |
| Step 2. Identify what you are looking for. | the measure of the third angle in a triangle |
| Step 3. Name. Choose a variable to represent it. | let x = the measure of the angle |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B+m∠C=180 |
| Step 5. Solve the equation. | 55+82+x=180137+x=180x=43 |
| Step 6. Check. | 55+82+43?=180180=180✓ |
| Step 7. Answer the question. | The measure of the third angle is 43 degrees. |
The measures of two angles of a triangle are 31° and 128°. Find the measure of the third angle.
- Answer
-
21°
A triangle has angles of 49° and 75°. Find the measure of the third angle.
- Answer
-
56°
Right Triangles
Some triangles have special names. We will look first at the right triangle. A right triangle has one 90° angle, which is often marked with the symbol shown in Figure 9.4.6.
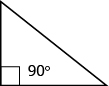
Figure 9.4.6
If we know that a triangle is a right triangle, we know that one angle measures 90° so we only need the measure of one of the other angles in order to determine the measure of the third angle.
One angle of a right triangle measures 28°. What is the measure of the third angle?
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 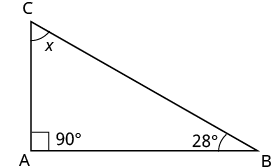 |
| Step 2. Identify what you are looking for. | the measure of an angle |
| Step 3. Name. Choose a variable to represent it. | let x = the measure of the angle |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B+m∠C=180 |
| Step 5. Solve the equation. | x+90+28=180x+118=180x=62 |
| Step 6. Check. | 180?=90+28+62180=180✓ |
| Step 7. Answer the question. | The measure of the third angle is 62°. |
One angle of a right triangle measures 56°. What is the measure of the other angle?
- Answer
-
34°
One angle of a right triangle measures 45°. What is the measure of the other angle?
- Answer
-
45°
In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.
The measure of one angle of a right triangle is 20° more than the measure of the smallest angle. Find the measures of all three angles.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the measures of all three angles |
| Step 3. Name. Choose a variable to represent it. Now draw the figure and label it with the given information. |
Let a = 1st angle a + 20 = 2nd angle 90 = 3rd angle (the right angle)
|
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. | m∠A+m∠B+m∠C=180a+(a+20)+90=180 |
| Step 5. Solve the equation. | 2a+110=1802a=70a=35firstanglea+20secondangle35+205590thirdangle |
| Step 6. Check. | 35+55+90?=180180=180✓ |
| Step 7. Answer the question. | The three angles measure 35°, 55°, and 90°. |
The measure of one angle of a right triangle is 50° more than the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
20°, 70°, 90°
The measure of one angle of a right triangle is 30° more than the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
30°, 60°, 90°
Similar Triangles
When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures. One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures.
The two triangles in Figure 9.4.7 are similar. Each side of ΔABC is four times the length of the corresponding side of ΔXYZ and their corresponding angles have equal measures.
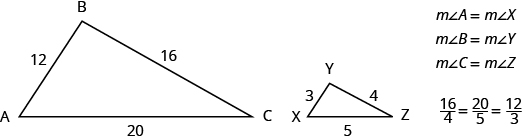
Figure 9.4.7 - ΔABC and ΔXYZ are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.
If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.
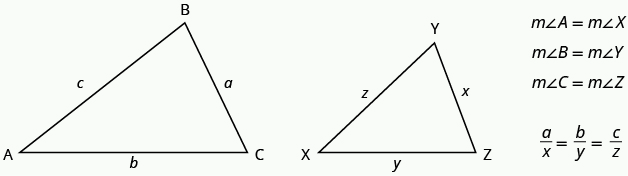
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in ΔABC:
the length a can also be written BC
the length b can also be written AC
the length c can also be written AB
We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.
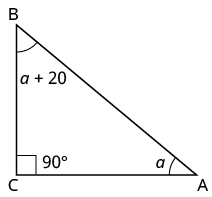
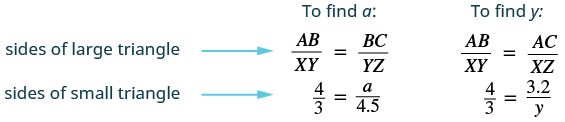
ΔABC and ΔXYZ are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.
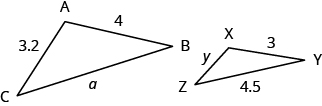
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | The figure is provided. |
| Step 2. Identify what you are looking for. | The length of the sides of similar triangles |
| Step 3. Name. Choose a variable to represent it. | Let a = length of the third side of ΔABC, y = length of the third side ΔXYZ |
| Step 4. Translate. |
The triangles are similar, so the corresponding sides are in the same ratio. SoABXY=BCYZ=ACXZSince the side AB = 4 corresponds to the side XY = 3 , we will use the ratio ABXY=43 to find the other sides. Be careful to match up corresponding sides correctly.
|
| Step 5. Solve the equation. | 3a=4(4.5)4y=3(3.2)3a=184y=9.6a=6y=2.4 |
| Step 6. Check. | 43?=64.543?=3.22.44(4.5)?=6(3)4(2.4)?=3.2(3)18=18✓9.6=9.6✓ |
| Step 7. Answer the question. | The third side of ΔABC is 6 and the third side of ΔXYZ is 2.4. |
ΔABC is similar to ΔXYZ. Find a.
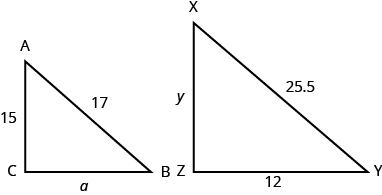
- Answer
-
a = 8
ΔABC is similar to ΔXYZ. Find y.

- Answer
-
y = 22.5
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."