12.3: Continuity
- Page ID
- 1405
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Arizona is known for its dry heat. On a particular day, the temperature might rise as high as \(118^∘F\) and drop down only to a brisk \(95^∘F.\) Figure \(\PageIndex{1}\) shows the function \(T\), where the output of \(T(x)\) is the temperature in Fahrenheit degrees and the input \(x\) is the time of day, using a 24-hour clock on a particular summer day.
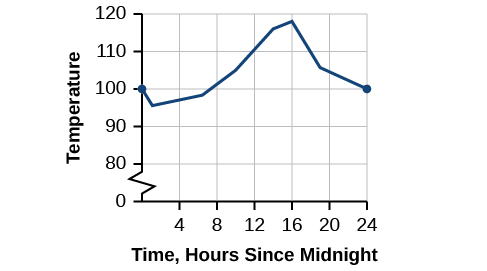
Figure \(\PageIndex{1}\): Temperature as a function of time forms a continuous function.
When we analyze this graph, we notice a specific characteristic. There are no breaks in the graph. We could trace the graph without picking up our pencil. This single observation tells us a great deal about the function. In this section, we will investigate functions with and without breaks.
Determining Whether a Function Is Continuous at a Number
Let’s consider a specific example of temperature in terms of date and location, such as June 27, 2013, in Phoenix, AZ. The graph in Figure \(\PageIndex{1}\) indicates that, at 2 a.m., the temperature was \(96 ^∘F\). By 2 p.m. the temperature had risen to \(116^∘F,\) and by 4 p.m. it was \(118 ^∘F.\) Sometime between 2 a.m. and 4 p.m., the temperature outside must have been exactly \(110.5 ^∘ F\). In fact, any temperature between \(96 ^∘ F\) and \(118 ^∘ F\) occurred at some point that day. This means all real numbers in the output between \(96 ^∘ F\) and \(118 ^∘ F\) are generated at some point by the function according to the intermediate value theorem,
Look again at Figure \(\PageIndex{1}\). There are no breaks in the function’s graph for this 24-hour period. At no point did the temperature cease to exist, nor was there a point at which the temperature jumped instantaneously by several degrees. A function that has no holes or breaks in its graph is known as a continuous function. Temperature as a function of time is an example of a continuous function.
If temperature represents a continuous function, what kind of function would not be continuous? Consider an example of dollars expressed as a function of hours of parking. Let’s create the function \(D\), where \(D(x)\) is the output representing cost in dollars for parking \(x\) number of hours (Figure \(\PageIndex{2}\)).
Suppose a parking garage charges $4.00 per hour or fraction of an hour, with a $25 per day maximum charge. Park for two hours and five minutes and the charge is $12. Park an additional hour and the charge is $16. We can never be charged $13, $14, or $15. There are real numbers between 12 and 16 that the function never outputs. There are breaks in the function’s graph for this 24-hour period, points at which the price of parking jumps instantaneously by several dollars.
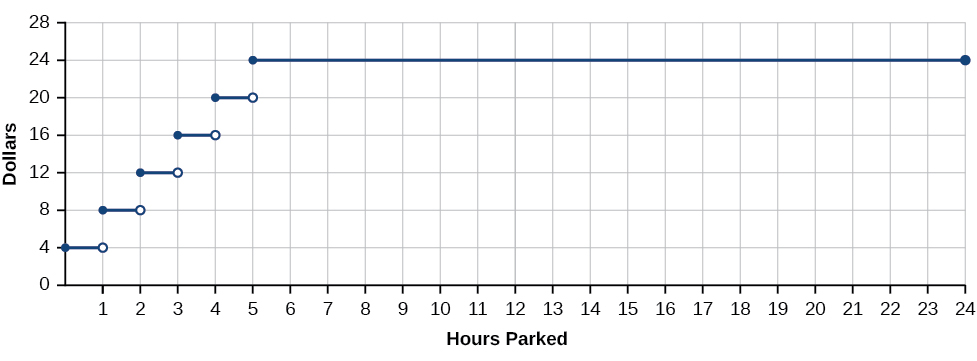
A function that remains level for an interval and then jumps instantaneously to a higher value is called a stepwise function. This function is an example.
A function that has any hole or break in its graph is known as a discontinuous function. A stepwise function, such as parking-garage charges as a function of hours parked, is an example of a discontinuous function.
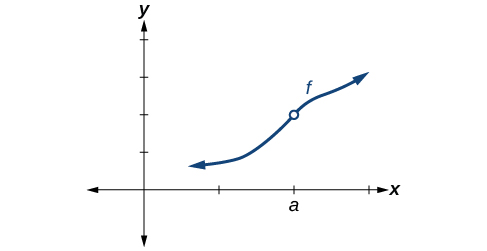
So how can we decide if a function is continuous at a particular number? We can check three different conditions. Let’s use the function \(y=f(x)\) represented in Figure as an example.
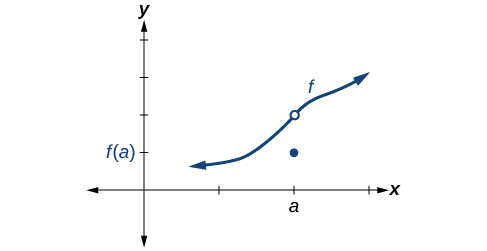
Condition 3 According to Condition 3, the corresponding y y coordinate at \(x=a\) fills in the hole in the graph of \(f\). This is written \(\lim \limits_{x \to a} f(x)=f(a)\).
Satisfying all three conditions means that the function is continuous. All three conditions are satisfied for the function represented in Figure so the function is continuous as \(x=a\).
All three conditions are satisfied. The function is continuous at \(x=a\).
Figure through Figure provide several examples of graphs of functions that are not continuous at \(x=a\) and the condition or conditions that fail.
Condition 2 is satisfied. Conditions 1 and 3 both fail.
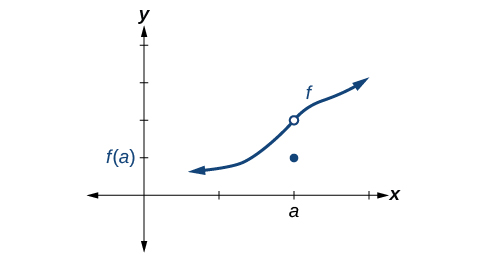
Conditions 1 and 2 are both satisfied. Condition 3 fails.
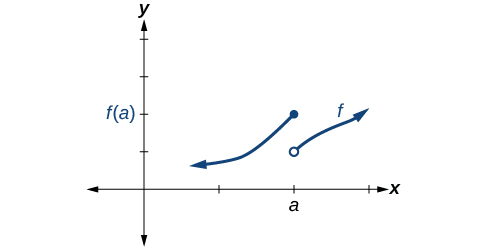
Condition 1 is satisfied. Conditions 2 and 3 fail.
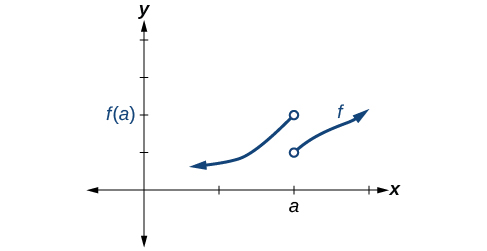
Conditions 1, 2, and 3 all fail.
Definition of continuity
A function \(f(x)\) is continuous at \(x=a\) provided all three of the following conditions hold true:
- Condition 1: \(f(a)\) exists.
- Condition 2: \(\lim \limits_{x \to a} f(x)\) exists at \(x=a\).
- Condition 3: \(\lim \limits_{x \to a} f(x)=f(a)\)
If a function \(f(x)\) is not continuous at \(x=a\),the function is discontinuous at \(x=a\).
Identifying a Jump Discontinuity
Discontinuity can occur in different ways. We saw in the previous section that a function could have a left-hand limit and a right-hand limit even if they are not equal. If the left- and right-hand limits exist but are different, the graph “jumps” at \(x=a\). The function is said to have a jump discontinuity.
As an example, look at the graph of the function \(y=f(x)\) in Figure. Notice as \(x\) approaches \(a\) how the output approaches different values from the left and from the right.
Graph of a function with a jump discontinuity.
JUMP DISCONTINUITY
A function \(f(x)\) has a jump discontinuity at \(x=a\) if the left- and right-hand limits both exist but are not equal: \( \lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)\)
Identifying Removable Discontinuity
Some functions have a discontinuity, but it is possible to redefine the function at that point to make it continuous. This type of function is said to have a removable discontinuity. Let’s look at the function \(y=f(x)\) represented by the graph in Figure. The function has a limit. However, there is a hole at \(x=a\). The hole can be filled by extending the domain to include the input \(x=a\) and defining the corresponding output of the function at that value as the limit of the function at \(x=a\).
Graph of function \(f\) with a removable discontinuity at \(x=a\).
removable discontinuity
A function f(x) f(x) has a removable discontinuity at \(x=a\) if the limit, \(\lim \limits_{x \to a} f(x),\) exists, but either
- \(f(a)\) does not exist or
- \(f(a)\), the value of the function at \(x=a\) does not equal the limit, \(f(a)≠ \lim \limits_{x \to a} f(x)\).
Example \(\PageIndex{1}\): Identifying Discontinuities
Identify all discontinuities for the following functions as either a jump or a removable discontinuity.
- \(f(x)=\frac{x^2−2x−15}{x−5}\)
- \[ g(x)= \begin{cases} x+1, & x<2 \\ −x, & x≥2 \end{cases} \]
- Notice that the function is defined everywhere except at \(x=5\).
Thus, \(f(5)\) does not exist, Condition 2 is not satisfied. Since Condition 1 is satisfied, the limit as \(x\) approaches 5 is 8, and Condition 2 is not satisfied.This means there is a removable discontinuity at \(x=5\).
- Condition 2 is satisfied because \(g(2)=−2.\)
Notice that the function is a piecewise function, and for each piece, the function is defined everywhere on its domain. Let’s examine Condition 1 by determining the left- and right-hand limits as \(x\) approaches 2.
Left-hand limit: \(\lim \limits_{x \to 2^−} (x+1)=2+1=3\). The left-hand limit exists.
Right-hand limit: \(\lim \limits_{x \to 2^+} (−x)=−2\). The right-hand limit exists. But
\[\lim \limits_{x \to 2^−} f(x)≠ \lim \limits_{x \to 2^+} f(x).\]
So, \(\lim \limits_{x \to 2} f(x)\) does not exist, and Condition 2 fails: There is no removable discontinuity. However, since both left- and right-hand limits exist but are not equal, the conditions are satisfied for a jump discontinuity at \(x=2\).
Exercise \(\PageIndex{1}\):
Identify all discontinuities for the following functions as either a jump or a removable discontinuity.
- \(f(x)=\frac{x^2−6x}{x−6}\)
- \(g(x)= \begin{cases} \sqrt{x}, & 0≤x<4 \\ 2x, & x≥4 \end{cases} \)
- removable discontinuity at \(x=6\);
- jump discontinuity at \(x=4\)
Recognizing Continuous and Discontinuous Real-Number Functions
Many of the functions we have encountered in earlier chapters are continuous everywhere. They never have a hole in them, and they never jump from one value to the next. For all of these functions, the limit of \(f(x)\) as \(x\) approaches a a is the same as the value of \(f(x)\) when \(x=a\). So \(\lim \limits_{x \to a} f(x)=f(a)\). There are some functions that are continuous everywhere and some that are only continuous where they are defined on their domain because they are not defined for all real numbers.
EXAMPLES OF CONTINUOUS FUNCTIONS
The following functions are continuous everywhere:
| Polynomial functions | Ex: \(f(x)=x^4−9x^2\) |
| Exponential functions | Ex: \(f(x)=4^{x+2}−5\) |
| Sine functions | Ex: \(f(x)=\sin (2x)−4\) |
| Cosine functions | Ex: \(f(x)=− \cos (x+\frac{π}{3})\) |
The following functions are continuous everywhere they are defined on their domain:
| Logarithmic functions | Ex: \(f(x)=2 \ln (x), x>0\) |
| Tangent functions | Ex: \(f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k\) is an integer |
| Rational functions | Ex: \(f(x)=\frac{x^2−25}{x−7}, x≠7\) |
how to:Given a function \(f(x)\), determine if the function is continuous at \(x=a\).
- Check Condition 1: \(f(a)\) exists.
- Check Condition 2: \(\lim \limits_{x \to a} f(x)\) exists at \(x=a\).
- Check Condition 3: \(\lim \limits_{x \to a} f(x)=f(a).\)
- If all three conditions are satisfied, the function is continuous at \(x=a\). If any one of the conditions is not satisfied, the function is not continuous at \(x=a\).
Example \(\PageIndex{2}\): Determining Whether a Piecewise Function is Continuous at a Given Number
Determine whether the function \(f(x)= \begin{cases} 4x, & x≤3 \\ 8+x, & x>3 \end{cases}\) is continuous at
- \(x=3\)
- \(x=\frac{8}{3}\)
To determine if the function \(f\) is continuous at \(x=a,\) we will determine if the three conditions of continuity are satisfied at \(x=a\).
- Condition 1: Does \(f(a)\) exist?
\[\begin{align} f(3)=4(3)=12 \\ ⇒ \text{Condition 1 is satisfied.} \end{align} \]
Condition 2: Does \(\lim \limits_{x \to 3} f(x)\) exist?
To the left of \(x=3, f(x)=4x;\) to the right of \(x=3, f(x)=8+x.\) We need to evaluate the left- and right-hand limits as \(x\) approaches 1.
- Left-hand limit: \(\lim \limits_{x \to 3^−} f(x)= \lim \limits_{x \to 3^−} 4(3)=12\)
- Right-hand limit: \(\lim \limits_{x \to 3^+} f(x)= \lim \limits_{x \to 3^+}(8+x)=8+3=11\)
Because \(\lim \limits_{x \to 1^−} f(x)≠ \lim \limits_{x \to 1^+} f(x), \lim \limits_{x \to 1} f(x)\) does not exist.
\[⇒ \text{Condition 2 fails.}\]
There is no need to proceed further. Condition 2 fails at \(x=3\). If any of the conditions of continuity are not satisfied at \(x=3\), the function \(f(x)\) is not continuous at \(x=3\).
- \(x=\frac{8}{3}\)
Condition 1: Does \(f(\frac{8}{3})\) exist?
\[\begin{align} f(\frac{8}{3})=4(\frac{8}{3})=\frac{32}{3} \\ ⇒\text{Condition 1 is satisfied.} \end{align}\]
Condition 2: Does \(\lim \limits_{x \to \frac{8}{3}} f(x)\) exist?
To the left of \(x=\frac{8}{3}\), \(f(x)=4x\); to the right of \(x=\frac{8}{3}, f(x)=8+x\). We need to evaluate the left- and right-hand limits as \(x\) approaches \(\frac{8}{3}\).
- Left-hand limit: \(\lim \limits_{x \to \frac{8}{3}^−} f(x)= \lim \limits_{x \to \frac{8}{3}^−} 4(\frac{8}{3})=\frac{32}{3}\)
- Right-hand limit: \(\lim \limits_{x \to \frac{8}{3}^+} f(x)= \lim \limits_{x \to \frac{8}{3}^+} (8+x)=8+\frac{8}{3}=\frac{32}{3}\)
Because \(\lim \limits_{x \to \frac{8}{3}} f(x)\) exists,
\[⇒ \text{Condition 2 is satisfied.}\]
Condition 3: Is \(f(\frac{8}{3})=\lim \limits_{x \to \frac{8}{3}} f(x)\)?
\[\begin{align} f(\frac{32}{3})=\frac{32}{3}=\lim \limits_{x \to \frac{8}{3}} f(x) \\ ⇒ \text{Condition 3 is satisfied.} \end{align}\]
Because all three conditions of continuity are satisfied at \(x=\frac{8}{3}\), the function \(f(x)\) is continuous at \(x=\frac{8}{3}\).
Exercise \(\PageIndex{2}\):
Determine whether the function \(f(x)= \begin{cases} & \frac{1}{x}, && x≤2 \\ & 9x−11.5, && x>2 \end{cases}\) is continuous at \(x=2\).
yes
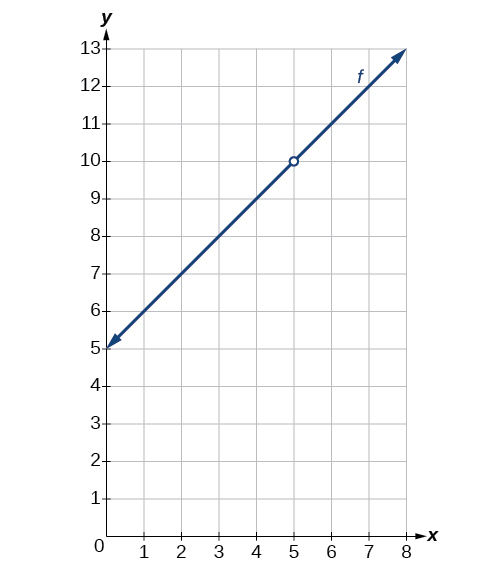
Example \(\PageIndex{3}\): Determining Whether a Rational Function is Continuous at a Given Number
Determine whether the function \(f(x)=\frac{x^2−25}{x−5}\) is continuous at \(x=5\).
To determine if the function \(f\) is continuous at \(x=5\), we will determine if the three conditions of continuity are satisfied at \(x=5\).
Condition 1:
\[\begin{align} f(5) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]
There is no need to proceed further. Condition 2 fails at \(x=5\). If any of the conditions of continuity are not satisfied at \(x=5\),the function f f is not continuous at \(x=5\).
Analysis
See Figure. Notice that for Condition 2 we have
\[\begin{align} \lim \limits_{x \to 5} \dfrac{x^2−25}{x−5} &= \lim \limits_{x \to 3} \dfrac{\cancel{(x−5)}(x+5)}{\cancel{x−5}} \\ &= \lim \limits_{x \to 5}(x+5) \\ &=5+5=10 \\ &⇒ \text{Condition 2 is satisfied.} \end{align}\]
At x=5, x=5,there exists a removable discontinuity. See Figure.
Exercise \(\PageIndex{3}\):
Determine whether the function \(f(x)=\frac{9−x^2}{x^2−3x}\) is continuous at \(x=3\). If not, state the type of discontinuity.
No, the function is not continuous at \(x=3\). There exists a removable discontinuity at \(x=3\).
Determining the Input Values for Which a Function Is Discontinuous
Now that we can identify continuous functions, jump discontinuities, and removable discontinuities, we will look at more complex functions to find discontinuities. Here, we will analyze a piecewise function to determine if any real numbers exist where the function is not continuous. A piecewise function may have discontinuities at the boundary points of the function as well as within the functions that make it up.
To determine the real numbers for which a piecewise function composed of polynomial functions is not continuous, recall that polynomial functions themselves are continuous on the set of real numbers. Any discontinuity would be at the boundary points. So we need to explore the three conditions of continuity at the boundary points of the piecewise function.
how to: Given a piecewise function, determine whether it is continuous at the boundary points
- For each boundary point \(a\) of the piecewise function, determine the left- and right-hand limits as \(x\) approaches \(a, \) as well as the function value at \(a\).
- Check each condition for each value to determine if all three conditions are satisfied.
- Determine whether each value satisfies condition 1: \(f(a)\) exists.
- Determine whether each value satisfies condition 2: \(\lim \limits_{x \to a} f(x)\) exists.
- Determine whether each value satisfies condition 3: \(\lim \limits_{x \to a} f(x)=f(a).\)
- If all three conditions are satisfied, the function is continuous at \(x=a\). If any one of the conditions fails, the function is not continuous at \(x=a\).
Example \(\PageIndex{4}\): Determining the Input Values for Which a Piecewise Function Is Discontinuous
Determine whether the function f f is discontinuous for any real numbers.
\[fx= \begin{cases} x+1, &x<2 \\ 3, &2≤x<4 \\ x^2−11, & x≥4 \end{cases} \]
Analysis
See Figure. At \(x=4\),there exists a jump discontinuity. Notice that the function is continuous at \(x=2\).
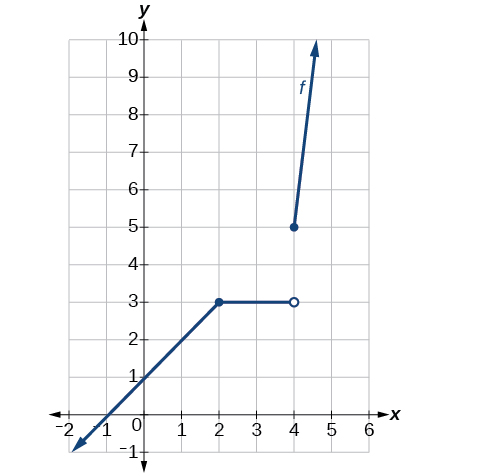
Graph is continuous at \(x=2\) but shows a jump discontinuity at \(x=4\).
Exercise \(\PageIndex{4}\):
Determine where the function \(f(x)= \begin{cases} \frac{πx}{4}, &x<2 \\ \frac{π}{x}, & 2≤x≤6 \\ 2πx, &x>6 \end{cases}\) is discontinuous.
\(x=6\)
Determining Whether a Function Is Continuous
To determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each of the functions that make up the piecewise function is continuous.
how to: Given a piecewise function, determine whether it is continuous.
- Determine whether each component function of the piecewise function is continuous. If there are discontinuities, do they occur within the domain where that component function is applied?
- For each boundary point \(x=a\) of the piecewise function, determine if each of the three conditions hold.
Example \(\PageIndex{5}\): Determining Whether a Piecewise Function Is Continuous
Determine whether the function below is continuous. If it is not, state the location and type of each discontinuity.
\[fx= \begin{cases} \sin (x), &x<0 \\ x^3, & x>0 \end{cases}\]
The two functions composing this piecewise function are \(f(x)=\sin (x)\) on \(x<0\) and \(f(x)=x^3\) on \(x>0\). The sine function and all polynomial functions are continuous everywhere. Any discontinuities would be at the boundary point,
At \(x=0\),let us check the three conditions of continuity.
Condition 1:
\[ \begin{align} f(0) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]
Because all three conditions are not satisfied at \(x=0\), the function \(f(x)\) is discontinuous at \(x=0\).
Analysis
See Figure. There exists a removable discontinuity at \(x=0\); \(\lim \limits_{x \to 0} f(x)=0\), thus the limit exists and is finite, but \(f(a)\) does not exist.
Function has removable discontinuity at 0.
Media
Access these online resources for additional instruction and practice with continuity.
Key Concepts
- A continuous function can be represented by a graph without holes or breaks.
- A function whose graph has holes is a discontinuous function.
- A function is continuous at a particular number if three conditions are met:
- Condition 1: \(f(a)\) exists.
- Condition 2: \(\lim \limits_{x \to a} f(x)\) exists at \(x=a\).
- Condition 3: \(\lim \limits_{x \to a} f(x)=f(a)\).
- A function has a jump discontinuity if the left- and right-hand limits are different, causing the graph to “jump.”
- A function has a removable discontinuity if it can be redefined at its discontinuous point to make it continuous. See Example.
- Some functions, such as polynomial functions, are continuous everywhere. Other functions, such as logarithmic functions, are continuous on their domain. See Example and Example.
- For a piecewise function to be continuous each piece must be continuous on its part of the domain and the function as a whole must be continuous at the boundaries. See Example and Example.
Glossary
- continuous function
- a function that has no holes or breaks in its graph
- discontinuous function
- a function that is not continuous at \(x=a\)
- jump discontinuity
- a point of discontinuity in a function \(f(x)\) at \(x=a\) where both the left and right-hand limits exist, but \(\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)\)
- removable discontinuity
- a point of discontinuity in a function \(f(x)\) where the function is discontinuous, but can be redefined to make it continuous


