3.3E: Graphs of Polynomial Functions (Exercises)

Last updated

Jan 2, 2021
Save as PDF
- 3.3: Graphs of Polynomial Functions
- 3.4: Factor Theorem and Remainder Theorem

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

section 3.3 exercise

Find the $C$ and $t$ intercepts of each function.

1. $C\left(t\right)=2\left(t-4\right)\left(t+1\right)(t-6)$

2. $C\left(t\right)=3\left(t+2\right)\left(t-3\right)(t+5)$

3. $C\left(t\right)=4t\left(t-2\right)^{2} (t+1)$

4. $C\left(t\right)=2t\left(t-3\right)\left(t+1\right)^{2}$

5. $C\left(t\right)=2t^{4} -8t^{3} +6t^{2}$

6. $C\left(t\right)=4t^{4} +12t^{3} -40t^{2}$

Use your calculator or other graphing technology to solve graphically for the zeros of the function.

7. $f\left(x\right)=x^{3} -7x^{2} +4x+30$

8. $g\left(x\right)=x^{3} -6x^{2} +x+28$

Find the long run behavior of each function as $t \to \infty$ and $t \to -\infty$

9. $h\left(t\right)=3\left(t-5\right)^{3} \left(t-3\right)^{3} (t-2)$

10. $k\left(t\right)=2\left(t-3\right)^{2} \left(t+1\right)^{3} (t+2)$

11. $p\left(t\right)=-2t\left(t-1\right)\left(3-t\right)^{2}$

12. $q\left(t\right)=-4t\left(2-t\right)\left(t+1\right)^{3}$

Sketch a graph of each equation.

13. $f\left(x\right)=\left(x+3\right)^{2} (x-2)$

14. $g\left(x\right)=\left(x+4\right)\left(x-1\right)^{2}$

15. $h\left(x\right)=\left(x-1\right)^{3} \left(x+3\right)^{2}$

16. $k\left(x\right)=\left(x-3\right)^{3} \left(x-2\right)^{2}$

17. $m\left(x\right)=-2x\left(x-1\right)(x+3)$

18. $n\left(x\right)=-3x\left(x+2\right)(x-4)$

Solve each inequality.

19. $\left(x-3\right)\left(x-2\right)^{2} >0$

20. $\left(x-5\right)\left(x+1\right)^{2} >0$

21. $\left(x-1\right)\left(x+2\right)\left(x-3\right)<0$

22. $\left(x-4\right)\left(x+3\right)\left(x+6\right)<0$

Find the domain of each function.

23. $f\left(x\right)=\sqrt{-42+19x-2x^{2} }$

24. $g\left(x\right)=\sqrt{28-17x-3x^{2} }$

25. $h\left(x\right)=\sqrt{4-5x+x^{2} }$

26. $k\left(x\right)=\sqrt{2+7x+3x^{2} }$

27. $n\left(x\right)=\sqrt{\left(x-3\right)\left(x+2\right)^{2} }$

28. $m\left(x\right)=\sqrt{\left(x-1\right)^{2} (x+3)}$

29. $p\left(t\right)=\dfrac{1}{t^{2} +2t-8}$

30. $q\left(t\right)=\dfrac{4}{x^{2} -4x-5}$

Write an equation for a polynomial the given features.

31. Degree 3. Zeros at $x$ = -2, $x$ = 1, and $x$ = 3. Vertical intercept at (0, -4)

32. Degree 3. Zeros at $x$ = -5, $x$ = -2, and $x$ = 1. Vertical intercept at (0, 6)

33. Degree 5. Roots of multiplicity 2 at $x$ = 3 and $x$ = 1, and a root of multiplicity 1 at $x$ = -3. Vertical intercept at (0, 9)

34. Degree 4. Root of multiplicity 2 at $x$ = 4, and a roots of multiplicity 1 at $x$ = 1 and $x$ = -2. Vertical intercept at (0, -3)

35. Degree 5. Double zero at $x$ = 1, and triple zero at $x$ = 3. Passes through the point (2, 15)

36. Degree 5. Single zero at $x$ = -2 and $x$ = 3, and triple zero at $x$ = 1. Passes through the point (2, 4)

Write a formula for each polynomial function graphed.

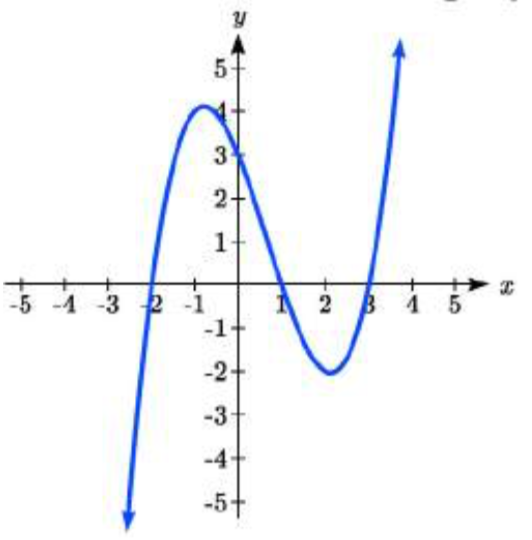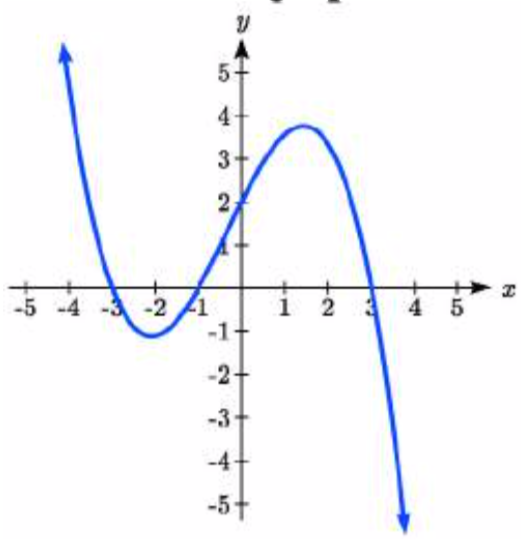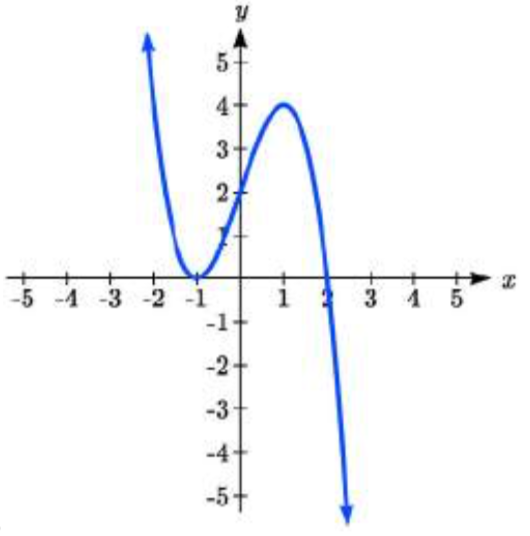
37. $屏幕快照 2019-06-23 上午3.24.15.png$ 38. $屏幕快照 2019-06-23 上午3.24.35.png$ 39. $屏幕快照 2019-06-23 上午3.24.57.png$

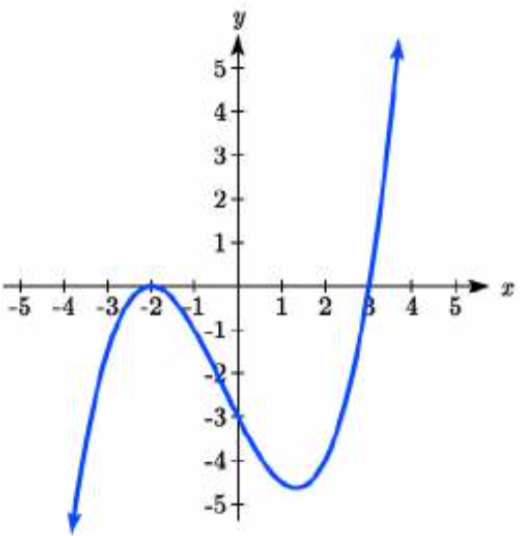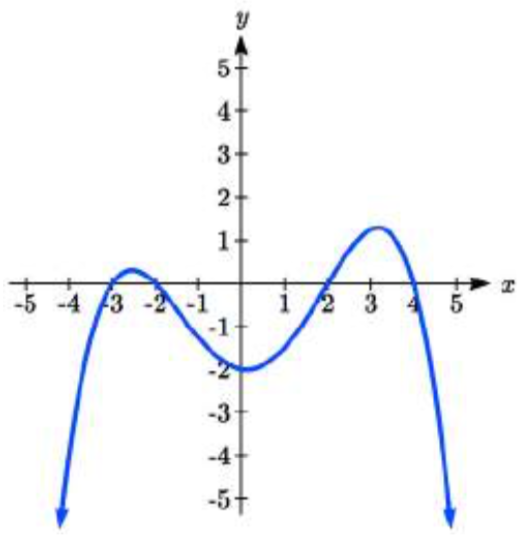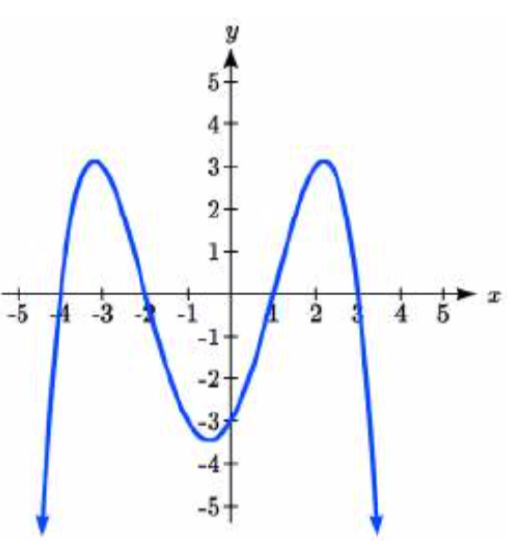
40. $屏幕快照 2019-06-23 上午3.25.18.png$ 41. $屏幕快照 2019-06-23 上午3.25.44.png$ 42. $屏幕快照 2019-06-23 上午3.26.12.png$

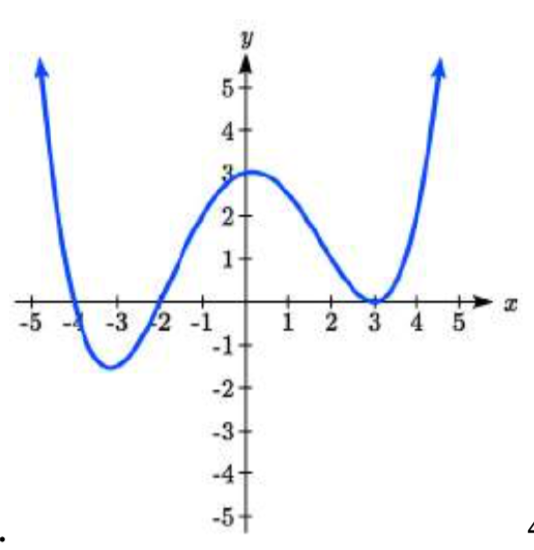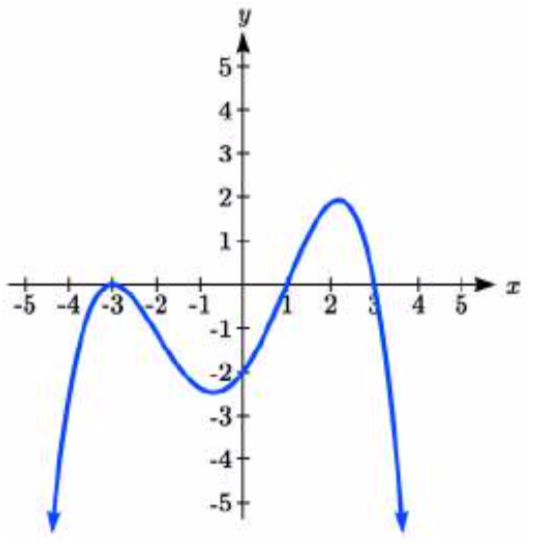
43. $屏幕快照 2019-06-23 上午3.26.29.png$ 44. $屏幕快照 2019-06-23 上午3.26.46.png$

Write a formula for each polynomial function graphed.

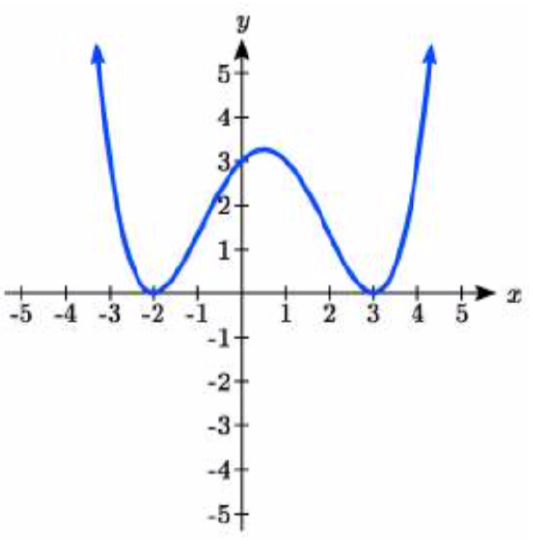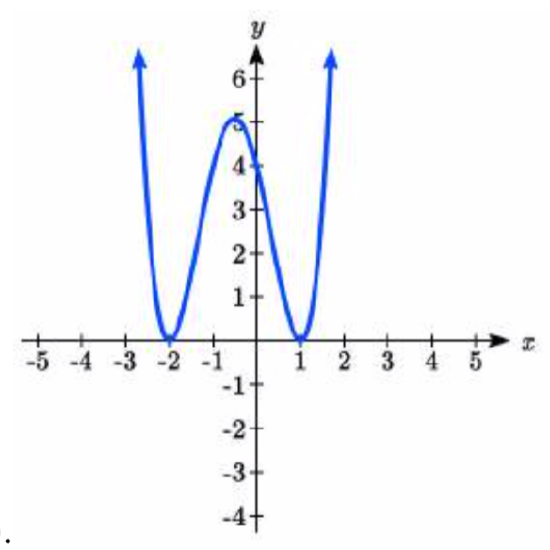
45. $屏幕快照 2019-06-23 上午5.32.03.png$ 46. $屏幕快照 2019-06-23 上午5.32.31.png$

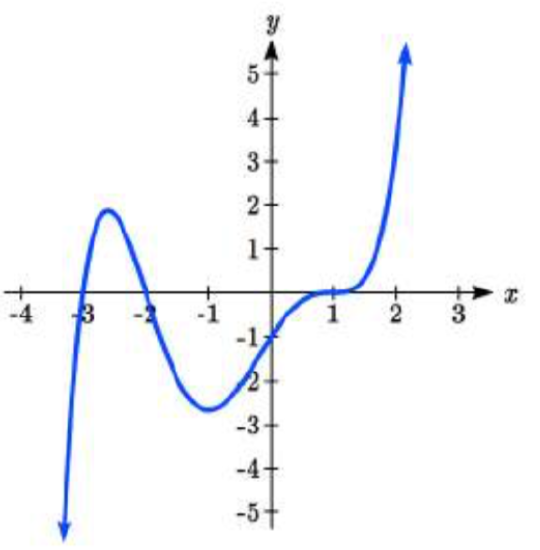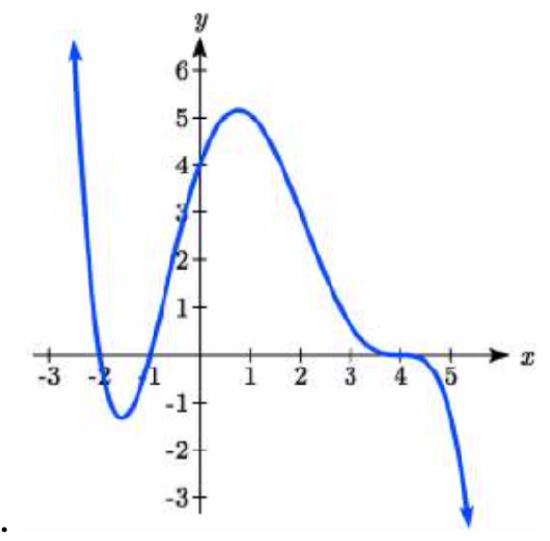
47. $屏幕快照 2019-06-23 上午5.32.47.png$ 48. $屏幕快照 2019-06-23 上午5.33.17.png$

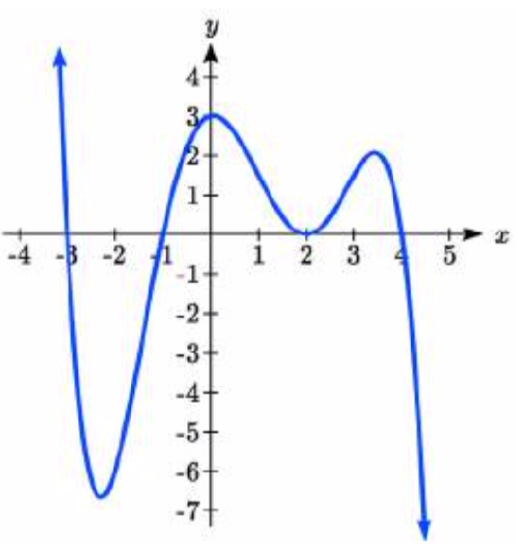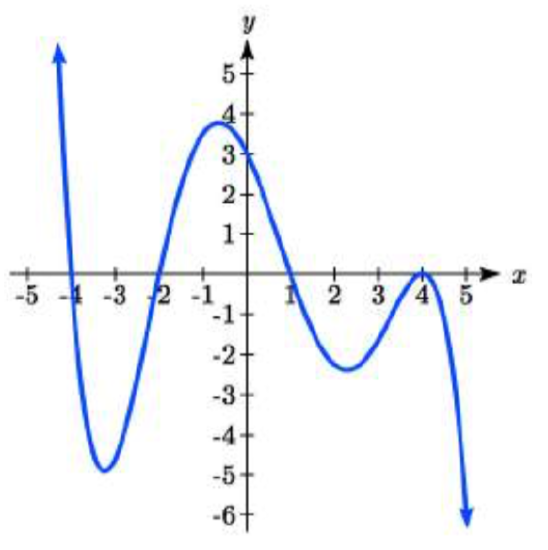
49. $屏幕快照 2019-06-23 上午5.33.39.png$ 50. $屏幕快照 2019-06-23 上午5.34.00.png$

51. A rectangle is inscribed with its base on the $x$ axis and its upper corners on the parabola $y=5-x^{2}$ . What are the dimensions of such a rectangle that has the greatest possible area?

52. A rectangle is inscribed with its base on the $x$ axis and its upper corners on the curve $y=16-x^{4}$ . What are the dimensions of such a rectangle that has the greatest possible area?

Answer

$C(t)$	$C$ , intercepts	$t$ , intercepts
1.	(0, 48)	(4, 0), (-1, 0), (6, 0)
3.	(0, 0)	(0, 0), (2, 0), (-1, 0)
5.	(0, 0)	(0, 0), (1, 0), (3, 0)

7. (-1.646, 0) (3.646, 0) (5, 0)

9. As $t \to \infty$ , $h(t) \to \infty$ $t \to -\infty$ , $h(t) \to -\infty$

11. As $t \to \infty$ , $p(t) \to -\infty$ $t \to -\infty$ , $p(t) \to -\infty$

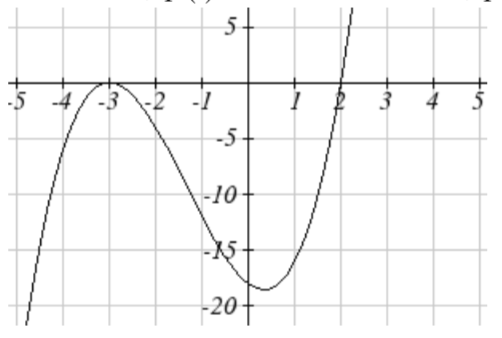
13. $Screen Shot 2019-10-03 at 6.05.35 PM.png$

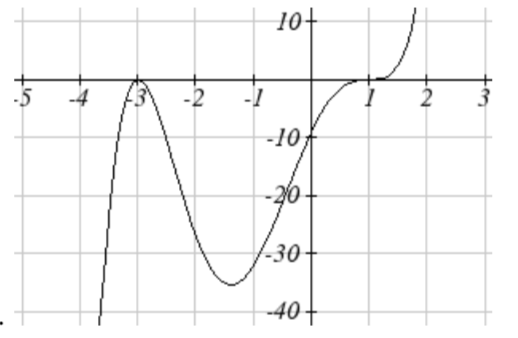
15. $Screen Shot 2019-10-03 at 6.05.54 PM.png$

17. $Screen Shot 2019-10-03 at 6.06.33 PM.png$

19. $(3, \infty)$

21. $(-\infty, -2) \cup (1, 3)$

23. [3, 5, 6]

25. $(-\infty, 1] \cup [4, \infty)$

27. $[-2, -2] \cup [3, \infty)$

29. $(-\infty, -4) \cup (-4, 2) \cup (2, \infty)$

31. $y = -\dfrac{2}{3} (x + 2) (x - 1) (x - 3)$

33. $y = \dfrac{1}{3} (x - 1)^2 (x - 3)^2 (x + 3)$

35. $y = -15(x - 1)^2 (x - 3)^2$

37. $y = \dfrac{1}{2} (x + 2)(x - 1) (x - 3)$

39. $y = -(x + 1)^2 (x - 2)$

41. $y = -\dfrac{1}{24} (x + 3)(x + 2) (x - 2) (x - 4)$

43. $y = \dfrac{1}{24} (x + 4) (x + 2) (x - 3)^2$

45. $y = \dfrac{1}{12} (x + 2)^2 (x - 3)^2$

47. $y = \dfrac{1}{6} (x + 3) (x + 2) (x - 1)^3$

49. $y = -\dfrac{1}{16} (x + 3)(x + 1) (x - 2)^2 (x - 4)$

51. Base 2.58, Height 3.336

Search

Text Color

Text Size

Margin Size

Font Type

Support Center

How can we help?