4.7E: Fitting Exponential Models to Data (Exercises)

Last updated

Jan 2, 2021
Save as PDF
- 4.7: Fitting Exponential Models to Data
- 5: Trigonometric Functions of Angles

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

section 4.7 exercise

Graph each function on a semi-log scale, then find a formula for the linearized function in the form $\log \left(f\left(x\right)\right)=mx+b$ .

1. $f\left(x\right)=4\left(1.3\right)^{x}$

2. $f\left(x\right)=2\left(1.5\right)^{x}$

3. $f\left(x\right)=10\left(0.2\right)^{x}$

4. $f\left(x\right)=30\left(0.7\right)^{x}$

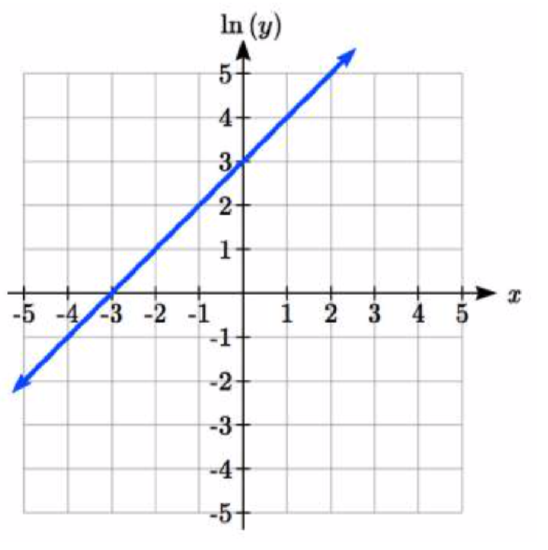
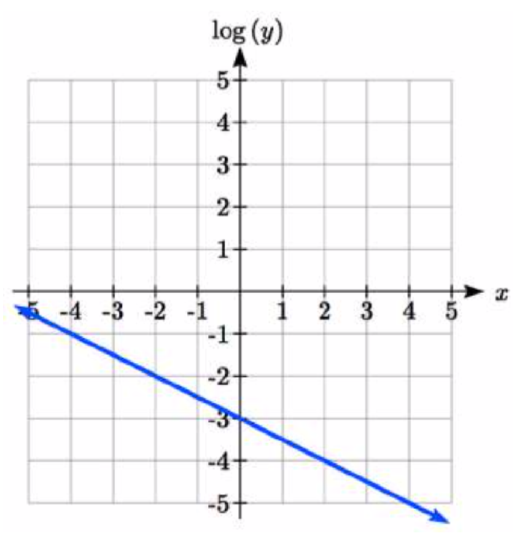
The graph below is on a semi-log scale, as indicated. Find a formula for the exponential function $y(x)$ .

5. 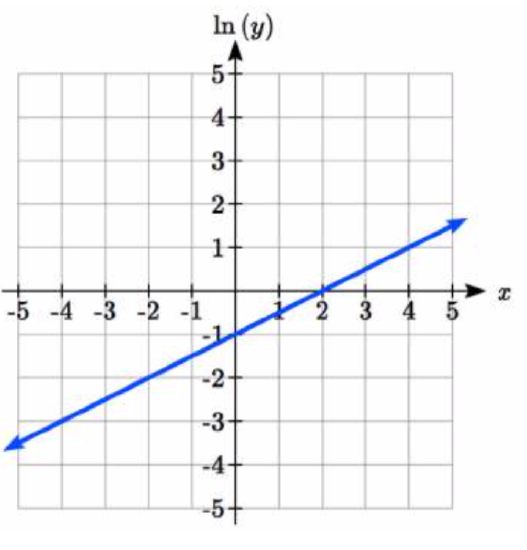$屏幕快照 2019-07-04 上午9.41.55.png$ 6. $屏幕快照 2019-07-04 上午9.42.43.png$

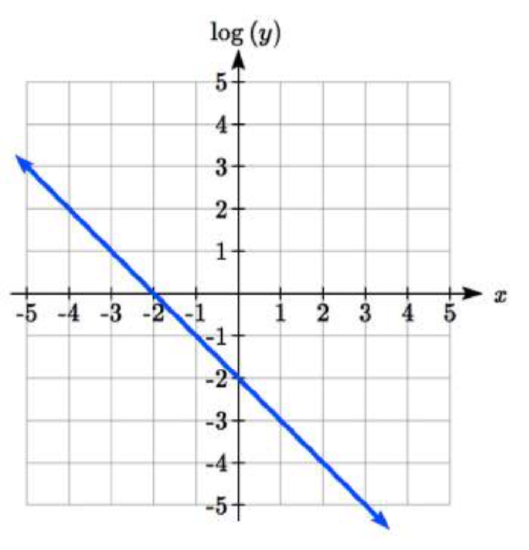7. $屏幕快照 2019-07-04 上午9.43.08.png$ 8. $屏幕快照 2019-07-04 上午9.43.52.png$

Use regression to find an exponential function that best fits the data given.

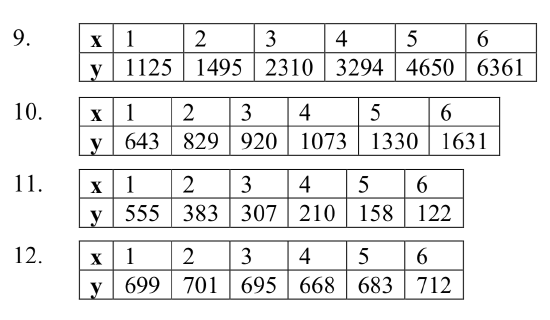
$屏幕快照 2019-07-04 上午9.44.11.png$

13. Total expenditures (in billions of dollars) in the US for nursing home care are shown below. Use regression to find an exponential function that models the data. What does the model predict expenditures will be in 2015?

Year	1990	1995	2000	2003	2005	2008
Expenditure	53	74	95	110	121	138

14. Light intensity as it passes through water decreases exponentially with depth. The data below shows the light intensity (in lumens) at various depths. Use regression to find an function that models the data. What does the model predict the intensity will be at 25 feet?

Depth (ft)	3	6	9	12	15	18
Lumen	11.5	8.6	6.7	5.2	3.8	2.9

15. The average price of electricity (in cents per kilowatt hour) from 1990 through 2008 is given below. Determine if a linear or exponential model better fits the data, and use the better model to predict the price of electricity in 2014.

Year	1986	1988	1990	1995	1997	2000	2002	2004	2006	2008
Cost	7.83	8.21	8.38	8.36	8.26	8.24	8.44	8.95	10.40	11.26

16. The average cost of a loaf of white bread from 1986 through 2008 is given below. Determine if a linear or exponential model better fits the data, and use the better model to predict the price of a loaf of bread in 2016.

Year	1986	1988	1990	1995	1997	2000	2002	2004	2006	2008
Cost	0.57	0.66	0.70	0.84	0.88	0.99	1.03	0.97	1.14	1.42

Answer

1. $\text{log} (f(x)) = \text{log} (1.3)x + \text{log} (4)$

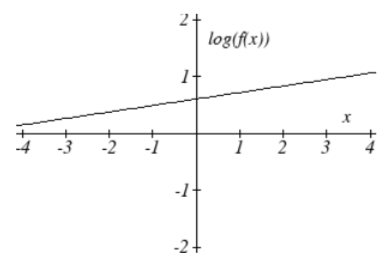
$Screen Shot 2019-10-04 at 3.06.47 PM.png$

3. $\text{log} (f(x)) = \text{log} (0.2) x + 1$

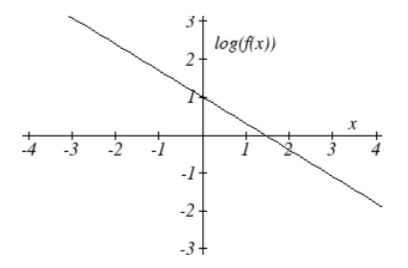
$Screen Shot 2019-10-04 at 3.07.22 PM.png$

5. $y = e^{\dfrac{1}{2}x - 1} = e^{-1} e^{\dfrac{1}{2}x} \approx 0.368 (1.6487)^x$

7. $y = 10^{-x - 2}. = 10^{-2} 10^{-1x} = 0.01 (0.1)^x$

9. $y = 776.682 (1.426)^x$

11. $y = 731.92(0.738)^x$

13. Expenditures are approximately $205

15. $y = 7.599(1.016)^x$ $r = 0.83064$ , $y = 0,1493x + 7.4893$ , $r = 0.81713$ . Using the better function, we predict electricity will be 11.157 cents per kwh

Search

Text Color

Text Size

Margin Size

Font Type

Support Center

How can we help?