7.4E: Modeling Changing Amplitude and Midline (Exercises)

Section 7.4 Exercises

Find a possible formula for the trigonometric function whose values are given in the following tables.

1.

	0	3	6	9	12	15	18
	-4	-1	2	-1	-4	-1	2

2.

	0	2	4	6	8	10	12
	5	1	-3	1	5	1	-3

3. The displacement , in centimeters, of a mass suspended by a spring is modeled by the function , where t is measured in seconds. Find the amplitude, period, and frequency of this displacement.

4. The displacement , in centimeters, of a mass suspended by a spring is modeled by the function , where is measured in seconds. Find the amplitude, period, and frequency of this displacement.

5. A population of rabbits oscillates 19 above and below average during the year, reaching the lowest value in January. The average population starts at 650 rabbits and increases by 160 each year. Find a function that models the population, , in terms of the months since January, .

6. A population of deer oscillates 15 above and below average during the year, reaching the lowest value in January. The average population starts at 800 deer and increases by 110 each year. Find a function that models the population, , in terms of the months since January, .

7. A population of muskrats oscillates 33 above and below average during the year, reaching the lowest value in January. The average population starts at 900 muskrats and increases by 7% each month. Find a function that models the population, , in terms of the months since January, .

8. A population of fish oscillates 40 above and below average during the year, reaching the lowest value in January. The average population starts at 800 fish and increases by 4% each month. Find a function that models the population, , in terms of the months since January, .

9. A spring is attached to the ceiling and pulled 10 cm down from equilibrium and released. The amplitude decreases by 15% each second. The spring oscillates 18 times each second. Find a function that models the distance, , the end of the spring is below equilibrium in terms of seconds, , since the spring was released.

10. A spring is attached to the ceiling and pulled 7 cm down from equilibrium and released. The amplitude decreases by 11% each second. The spring oscillates 20 times each second. Find a function that models the distance, , the end of the spring is below equilibrium in terms of seconds, , since the spring was released.

11. A spring is attached to the ceiling and pulled 17 cm down from equilibrium and released. After 3 seconds the amplitude has decreased to 13 cm. The spring oscillates 14 times each second. Find a function that models the distance, the end of the spring is below equilibrium in terms of seconds, , since the spring was released.

12. A spring is attached to the ceiling and pulled 19 cm down from equilibrium and released. After 4 seconds the amplitude has decreased to 14 cm. The spring oscillates 13 times each second. Find a function that models the distance, the end of the spring is below equilibrium in terms of seconds, , since the spring was released.

Match each equation form with one of the graphs.

13. a.
b.

14. a.
b.

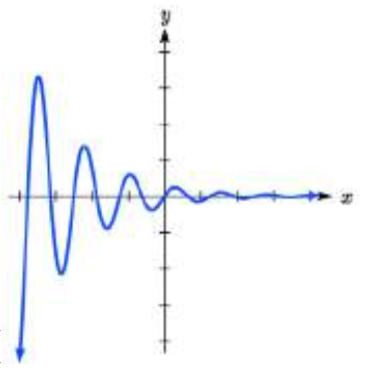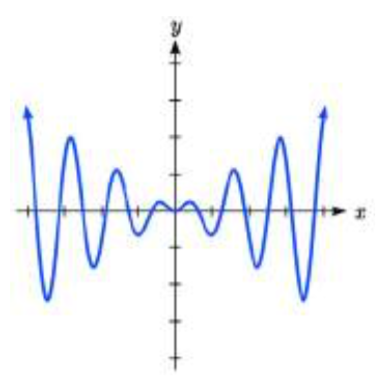I II III 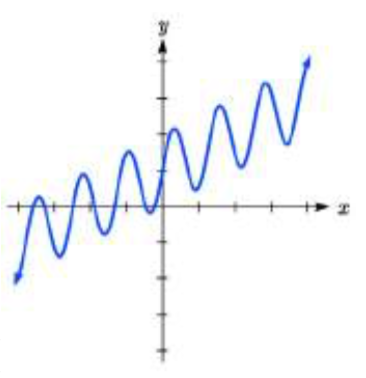IV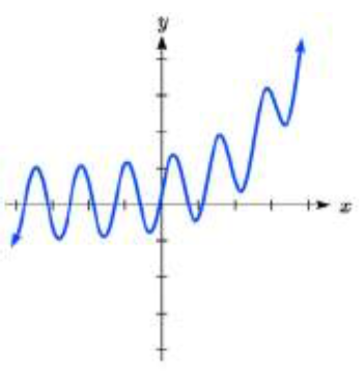

Find a function of the form that fits the data given.

15.

	0	1	2	3
	6	29	96	379

16.

	0	1	2	3
	6	34	150	746

Find a function of the form that fits the data given.

17.

	0	1	2	3
	7	6	11	16

18.

	0	1	2	3
	-2	6	4	2

Find a function of the form that fits the data given.

19.

	0	1	2	3
	11	3	1	3

20.

	0	1	2	3
	4	1	-11	1

Answer

1.

3. Amplitude: 8, Period: second, Frequency: 3 Hz (cycles per second)

5.

7.

9.

11.

13. a. IV
b. III

15.

17.

19.