8.1: Non-Right Triangles - Laws of Sines and Cosines
( \newcommand{\kernel}{\mathrm{null}\,}\)
Although right triangles allow us to solve many applications, it is more common to find scenarios where the triangle we are interested in does not have a right angle.
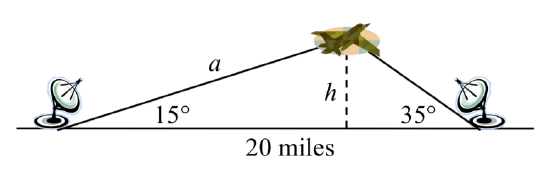
Two radar stations located 20 miles apart both detect a UFO located between them. The angle of elevatio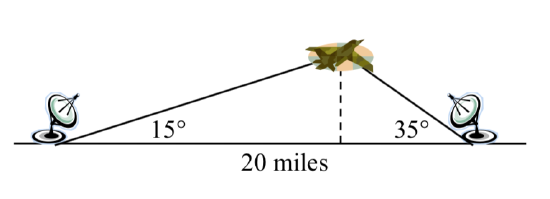 n measured by the first station is 35 degrees. The angle of elevation measured by the second station is 15 degrees. What is the altitude of the UFO?
n measured by the first station is 35 degrees. The angle of elevation measured by the second station is 15 degrees. What is the altitude of the UFO?
We see that the triangle formed by the UFO and the two stations is not a right triangle. Of course, in any triangle we could draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles, but it would be nice to have methods for working directly with non-right triangles. In this section, we will expand upon the right triangle trigonometry we learned in Chapter 5, and adapt it to non-right triangles.
Law of Sines
Given an arbitrary non-right triangle, we can drop an altitude, which we temporarily label h, to create two right triangles.
Using the right triangle relationships,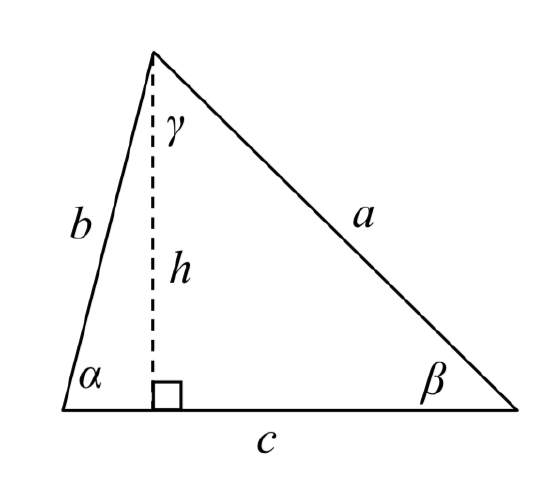
sin(α)=hb and sin(β)=ha
Solving both equations for h, we get bsin(α)=h and asin(β)=h. Since the h is the same in both equations, we establish bsin(α)=asin(β). Dividing both sides by ab, we conclude that
sin(α)a=sin(β)b
Had we drawn the altitude to be perpendicular to side b or a, we could similarly establish
sin(α)a=sin(γ)c and sin(β)b=sin(γ)c
Collectively, these relationships are called the Law of Sines.
LAW OF SINES
Given a triangle with angles and sides opposite labeled as shown, the ratio of sine of angle to length of the opposite side will always be equal, or, symbolically,
sin(α)a=sin(β)b=sin(γ)c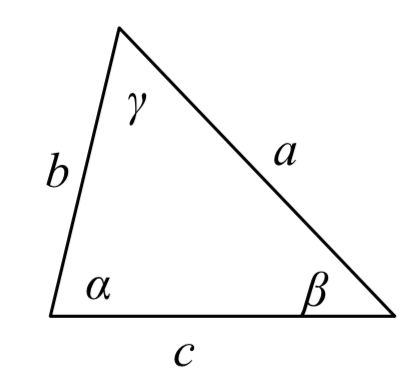
For clarity, we call side a the corresponding side of angle α.
Similarly, we call angle α, the corresponding angle of side a.
Likewise for side b and angle β, and for side c and angle γ.
When we use the law of sines, we use any pair of ratios as an equation. In the most straightforward case, we know two angles and one of the corresponding sides.
Example 8.1.1
In the triangle shown here, solve for the unknown sides and angle.
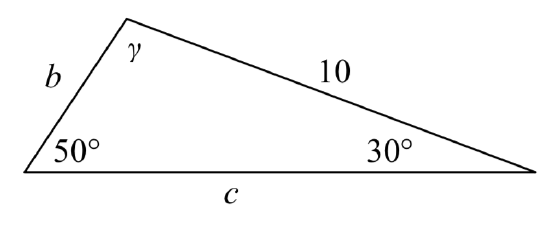
Solution
Solving for the unknown angle is relatively easy, since the three angles must add to 180 degrees.
From this, we can determine that
γ=180∘−50∘−30∘=100∘
To find an unknown side, we need to know the corresponding angle, and we also need another known ratio.
Since we know the angle 50∘ and its corresponding side, we can use this for one of the two ratios. To look for side b, we would use its corresponding angle, 30∘.
sin(50∘)10=sin(30∘)bMultiply both sides by b
bsin(50∘)10=sin(30∘)Divide, or multiply by the reciprocal, to solve for b
b=sin(30∘)10sin(50∘)≈6.527
Similarly, to solve for side c, we set up the equation
sin(50∘)10=sin(100∘)c
c=sin(100∘)10sin(50∘)≈12.856
Example 8.1.2
Find the elevation of the UFO from the beginning of the section.
Solution
To find the elevation of the UFO, we first find the distance from one station to the UFO, such as the side a in the picture, then use right triangle relationships to find the height of the UFO, h.
Since the angles in the triangle add to 180 degrees, the unknown angle of the triangle must be 180∘−15∘−35∘=130∘. This angle is opposite the side of length 20, allowing us to set up a Law of Sines relationship:
sin(130∘)20=sin(35∘)aMultiply by a
asin(130∘)20=sin(35∘)Divide, or multiply by the reciprocal, to solve for a
a=20sin(35∘)sin(130∘)≈14.975Simplify
The distance from one station to the UFO is about 15 miles. Now that we know a, we can use right triangle relationships to solve for h.
sin(15∘)=oppositehypotenuse=ha=h14.975Solve for h
h=14.975sin(15∘)≈3.876
The UFO is at an altitude of 3.876 miles.
In addition to solving triangles in which two angles are known, the law of sines can be used to solve for an angle when two sides and one corresponding angle are known.
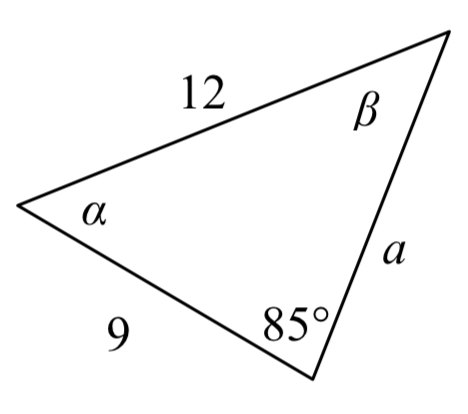
Example 8.1.3
In the triangle shown here, solve for the unknown sides and angles.
Solution
In choosing which pair of ratios from the Law of Sines to use, we always want to pick a pair where we know three of the four pieces of information in the equation. In this case, we know the angle 85∘ and its corresponding side, so we will use that ratio. Since our only other known information is the side with length 9, we will use that side and solve for its corresponding angle.
sin(85∘)12=sin(β)9Isolate the unknown
9sin(85∘)12=sin(β)Use the inverse sine to find a first solution
Remember when we use the inverse function that there are two possible answers.
β=sin−1(9sin(85∘)12)≈48.3438∘By symmetry we find the second possible solution
β=180∘−48.3438∘=131.6562∘
In this second case, if β≈132∘, then α would be α=180∘−85∘−132∘=−37∘, which doesn’t make sense, so the only possibility for this triangle is β=48.3438∘.
With a second angle, we can now easily find the third angle, since the angles must add to 180∘, so α=180∘–85∘–48.3438∘=46.6562∘.
Now that we know α, we can proceed as in earlier examples to find the unknown side a.
sin(85∘)12=sin(46.6562∘)a
a=12sin(46.6562∘)sin(85∘)≈8.7603
Notice that in the problem above, when we use Law of Sines to solve for an unknown angle, there can be two possible solutions. This is called the ambiguous case, and can arise when we know two sides and a non-included angle. In the ambiguous case we may find that a particular set of given information can lead to 2, 1 or no solution at all. However, when an accurate picture of the triangle or suitable context is available, we can determine which angle is desired.
Exercise 8.1.1
Given α=80∘,a=120,andb=121, find the corresponding and missing side and angles. If there is more than one possible solution, show both.
- Answer
-
sin(80∘)120=sin(β)121
1st possible solution β=83.2∘γ=16.8∘c=35.2
2nd solution β=96.8∘γ=3.2∘c=6.9
If we were given a picture of the triangle it may be possible to eliminate one of these
Example 8.1.4
Find all possible triangles if one side has length 4 opposite an angle of 50∘ and a second side has length 10.
Solution
Using the given information, we can look for the angle opposite the side of length 10.
sin(50∘)4=sin(α)10
sin(α)=10sin(50∘)4≈1.915
Since the range of the sine function is [-1, 1], it is impossible for the sine value to be 1.915. There are no triangles that can be drawn with the provided dimensions.
Example 8.1.5
Find all possible triangles if one side has length 6 opposite an angle of 50circ and a second side has length 4.
Solution
Using the given information, we can look for the angle opposite the side of length 4.
sin(50∘)6=sin(α)4
sin(α)=4sin(50∘)6≈0.511Use the inverse to find one solution
α=sin−1(0.511)≈30.710∘By symmetry there is a second possible solution
α=180∘−30.710∘=149.290∘
If we use the angle 30.710∘, the third angle would be 180∘−50∘−30.710∘=99.290∘. We can then use Law of Sines again to find the third side.
sin(50∘)6=sin(99.290∘)cSolve for c
c=7.730
If we used the angle α=149.290∘, the third angle would be 180∘–50∘–149.290∘=–19.29∘, which is impossible, so the previous triangle is the only possible one.
Exercise 8.1.2
Given α=80∘,a=100,andb=10 find the missing side and angles. If there is more than one possible solution, show both.
- Answer
-
sin(80∘)120=sin(β)10β=5.65∘ or β=174.35∘; only the first is reasonable.
γ=180∘−5.65∘−80∘=94.35∘
sin(80∘)120=sin(94.35∘)c
β=5.65∘,γ=94.35∘,c=101.25
Law of Cosines
Suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far from port is the boat?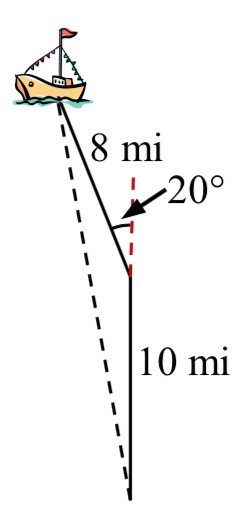
Unfortunately, while the Law of Sines lets us address many non-right triangle cases, it does not allow us to address triangles where the one known angle is included between two known sides, which means it is not a corresponding angle for a known side. For this, we need another tool.
Given an arbitrary non-right triangle, we can drop an altitude, which we te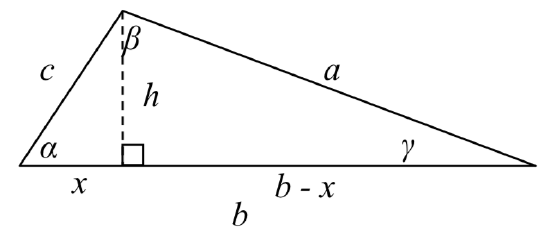 mporarily label h, to create two right triangles. We will divide the base b into two pieces, one of which we will temporarily label x.
mporarily label h, to create two right triangles. We will divide the base b into two pieces, one of which we will temporarily label x.
From this picture, we can establish the right triangle relationship
cos(α)=xc or equivalently,x=ccos(α)
Using the Pythagorean Theorem, we can establish
(b−x)2+h2=a2 and x2+h2=c2
Both of these equations can be solved for h2
h2=a2−(b−x)2 and h2=c2−x2
Since the left side of each equation is h2, the right sides must be equal
c2−x2=a2−(b−x)2Multiply out the right
c2−x2=a2−(b2−2bx+x2)Simplify
c2−x2=a2−b2+2bx−x2
c2=a2−b2+2bxIsolate a2
a2=c2+b2−2bxSubstitute in ccos(α)=x from above
a2=c2+b2−2bccos(α)
This result is called the Law of Cosines. Depending upon which side we dropped the altitude down from, we could have established this relationship using any of the angles. The important thing to note is that the right side of the equation involves an angle and the sides adjacent to that angle – the left side of the equation involves the side opposite that angle.
LAW OF COSINES
Given a triangle with angles and opposite sides labeled as shown,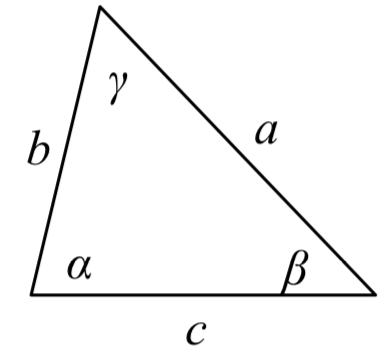
a2=c2+b2−2bccos(α)
b2=a2+c2−2accos(β)
c2=a2+b2−2abcos(γ)
Notice that if one of the angles of the triangle is 90 degrees, cos(90circ) = 0, so the formula
c2=a2+b2−2abcos(90∘)Simplifies to
c2=a2+b2
You should recognize this as the Pythagorean Theorem. Indeed, the Law of Cosines is sometimes called the Generalized Pythagorean Theorem, since it extends the Pythagorean Theorem to non-right triangles.
Example 8.1.6
Returning to our question from earlier, suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far from port is the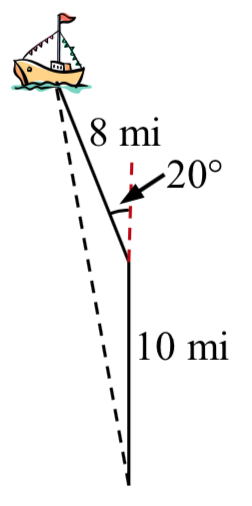 boat?
boat?
Solution
The boat turned 20 degrees, so the obtuse angle of the non-right triangle shown in the picture is the supplemental angle, 180∘−20∘=160∘.
With this, we can utilize the Law of Cosines to find the missing side of the obtuse triangle – the distance from the boat to port.
x2=82+102−2(8)(10)cos(160∘)Evaluate the cosine and simplify
x2=314.3508Square root both sides
x=√314.3508=17.730
The boat is 17.73 miles from port.
Example 8.1.7
Find the unknown side and angles of this triangle.
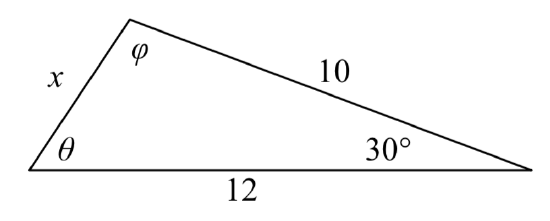
Solution
Notice that we don’t have both pieces of any side/angle pair, so the Law of Sines would not work with this triangle.
Since we have the angle included between the two known sides, we can turn to Law of Cosines.
Since the left side of any of the Law of Cosines equations involves the side opposite the known angle, the left side in this situation will involve the side x. The other two sides can be used in either order.
x2=102+122−2(10)(12)cos(30∘)Evaluate the cosine
x2=102+122−2(10)(12)√32Simplify
x2=244−120√3Take the square root
x=√244−120√3≈6.013
Now that we know an angle and its corresponding side, we can use the Law of Sines to fill in the remaining angles of the triangle. Solving for angle θ,
sin(30∘)6.013=sin(θ)10
sin(θ)=10sin(30∘)6.013Use the inverse sine
θ=sin−1(10sin(30∘)6.013)≈56.256∘
The other possibility for θ would be θ=180∘–56.256∘=123.744∘. In the original picture, θ is an acute angle, so 123.744°∘ doesn’t make sense if we assume the picture is drawn to scale.
Proceeding with θ=56.256∘, we can then find the third angle of the triangle:
ϕ=180∘−30∘−56.256∘=93.744∘
In addition to solving for the missing side opposite one known angle, the Law of Cosines allows us to find the angles of a triangle when we know all three sides.
Example 8.1.8
Solve for the angle α in the triangle shown.
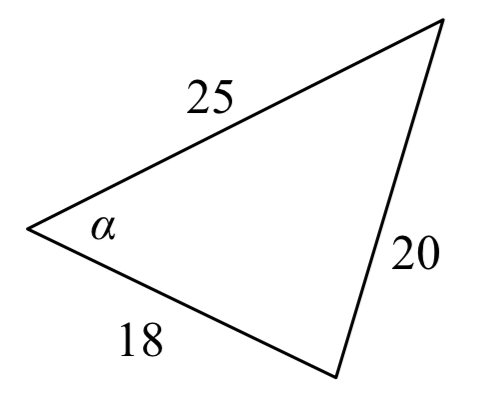
Solution
Using the Law of Cosines,
202=182+252−2(18)(25)cos(α)Simplify
400=949−900cos(α)
−549=−900cos(α)
−549−900=cos(α)
α=cos−1(−549−900)≈52.410∘
Exercise 8.1.3
Given α=25∘,b=10,andc=20find the missing side and angles.
- Answer
-
a2=102+202−2(10)(20)cos(25∘)a=11.725
sin(25∘)11.725=sin(β)10β=21.1∘ or β=158.9∘
only the first is reasonable since 25° + 158.9° would exceed 180°.
γ=180∘−21.1∘−25∘=133.9∘
β=21.1∘,γ=133.9∘,a=11.725
Notice that since the inverse cosine can return any angle between 0 and 180 degrees, there will not be any ambiguous cases when using Law of Cosines to find an angle.
Example 8.1.9
On many cell phones with GPS, an approximate location can be given before the GPS signal is received. This is done by a process called triangulation, which works by using the distance from two known points. Suppose there are two cell phone towers within range of you, located 6000 feet apart along a straight highway that runs east to west, and you know you are north of the highway. Based on the signal delay, it can be determined you are 5050 feet from the first tower, and 2420 feet from the second. Determine your position north and east of the first tower, and determine how far you are from the highway.
Solution
For simplicity, we start by drawing a picture and labeling our given information. Using the Law of Cosines, we can solve f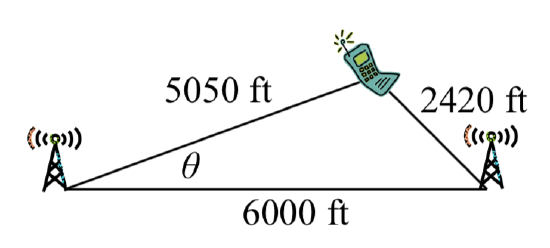 or the angle θ.
or the angle θ.
24202=60002+50502−2(5050)(6000)cos(θ)
5856400=61501500−60600000cos(θ)
−554646100=−60600000cos(θ)
cos(θ)=−554646100−60600000=0.9183
θ=cos−1(0.9183)=23.328∘
Using this angle, we could then use right triangles to find the position of the cell phone relative to the western tower.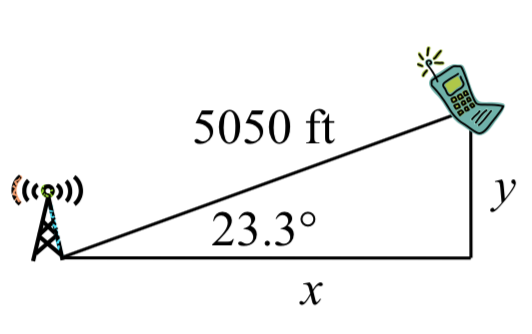
cos(23.328∘)=x5050
x=5050cos(23.328∘)≈4637.2 feet
sin(23.328∘)=y5050
y=5050sin(23.328∘)≈1999.8 feet
You are 5050 ft from the tower and 23.328∘ north of east (or, equivalently, 66.672° east of north). Specifically, you are about 4637 feet east and 2000 feet north of the first tower.
Note that if you didn’t know whether you were north or south of the towers, our calculations would have given two possible locations, one north of the highway and one south. To resolve this ambiguity in real world situations, locating a position using triangulation requires a signal from a third tower.
Example 8.1.10
To measure the height of a hill, a woman measures the angle of elevation to the top of the hill to be 24 degrees. She then moves back 200 feet and measures the angle of elevation to be 22 degrees. Find the height of the hill.
Solution
As with many problems of this nature, it will be helpful to draw a picture.
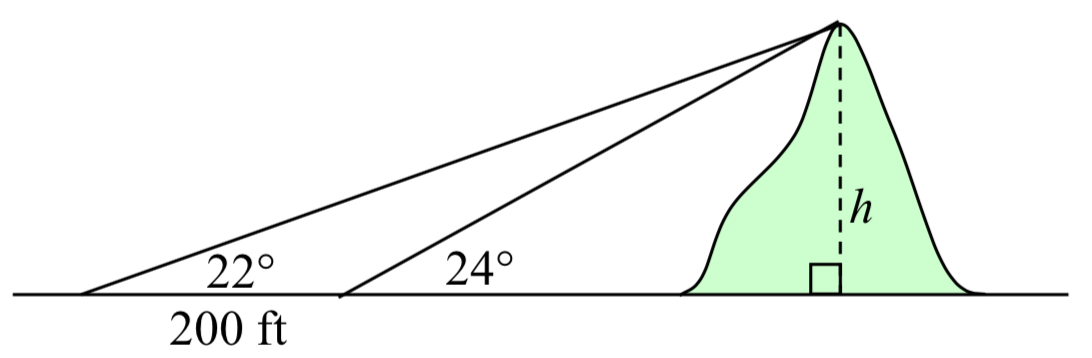
Notice there are three triangles formed here – the right triangle including the height h and the 22 degree angle, the right triangle including the height h and the 24 degree angle, and the (non-right) obtuse triangle including the 200 ft side. Since this is the triangle we have the most information for, we will begin with it. It may seem odd to work with this triangle since it does not include the desired side h, but we don’t have enough information to work with either of the right triangles yet.
We can find the obtuse angle of the triangle, since it and the angle of 24 degrees complete a straight line – a 180 degree angle. The obtuse angle must be 180∘−24∘=156∘. From this, we can determine that the third angle is 2∘. We know one side is 200 feet, and its corresponding angle is 2∘, so by introducing a temporary variable x for one of the other sides (as shown below), we can use Law of Sines to solve for this length x.
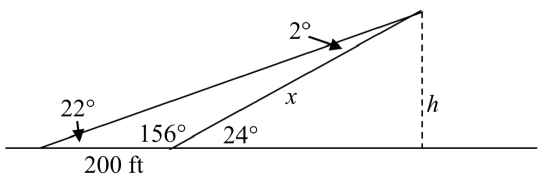
xsin(22∘)=200sin(2∘)Setting up the Law of Sines
x=sin(22∘)200sin(2∘)isolating the x value
x=2146.77 ft
Now that we know x, we can use right triangle properties to solve for h.
sin(24∘)=oppositehypotenuse=hx=h2146.77
h=2146.77sin(24∘)=873.17 ft The hill is 873 feet high.
Important Topics of This Section
- Law of Sines
Solving for sides
Solving for angles
Ambiguous case, 0, 1 or 2 solutions - Law of Cosines
Solving for sides
Solving for angles - Generalized Pythagorean Theorem


