2.5: Inverse Trignometric Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- Why doesn’t the sine function really have an inverse? What do we mean, then, by the inverse sine function? In other words, how is the inverse sine function defined?
- How is the inverse cosine function defined?
- How is the inverse tangent function defined?
Beginning Activity
- If y=5x+7 and y=4, what is the value of x?
- If y=√x and y=2.5, what is the value of x?
- If y=x2 and y=25, what are the possible values of x?
- If y=sin(x) and y=1, find two values for x with 0≤x≤2.2
Introduction
The work in the beginning activity illustrates the general problem that if we are given a function f and y=f(x), can we find the values of x if we know the value of y. In effect, this means that if we know the value of y, can we solve for the value of x? For the first problem, we can substitute y=4 into y=5x+7 and solve for x. This gives 4=5x+7
For the second and third problems, we have 2.5=√x
The work with the equation x2=25 shows that we can have more than one solution for this type of problem. With trigonometric functions, we can even have more solutions. For example, if y=sin(x) and y=12, we have sin(x)=12
If we restrict the values of 0≤x≤2π, there will be two solutions as shown in Figure 2.32
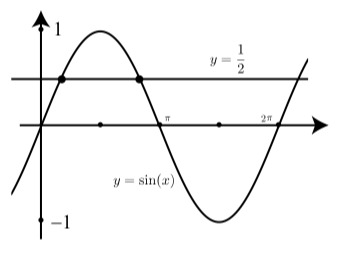
Figure 2.5.1: Graph Showing sin(x)=12
From our knowledge of the common arcs and reference arcs, these two solutions are x=π6 and x=5π6. In addition, the periodic nature of the sine function tells us that if there are no restrictions on x, there will be infinitely many solutions of the equation sin(x)=12. What we want to develop is a method to indicate exactly one of these solutions. But which one do we choose?
We have done something like this when we solve an equation such as x2=25. There are two solutions to this equation, but we have a function (the square root function) that gives us exactly one of these two functions. So when we write x=√25=5, we are specifying only the positive solution of the equation. If we want the other solution, we have to write x=−√25=−5. Notice that we used the square root function to designate the “simpler” of the two functions, namely the positive solution.
For the sine function, what we want is an inverse sine function that does just what the name suggests – uniquely reverses what the sine function does. That is, the inverse sine function takes a value from the range of the sine function and gives us exactly one arc whose sine has that value. We will try to do this in as simple of a manner as possible. (It may sometimes be hard to believe, but mathematicians generally do try to keep things simple.) To be more specific, if we have y=sin(x), we want to be able to specify any value for y with −1≤y≤1 and obtain one value for x. We will choose the value for x that is as close to 0 as possible. (Keep it simple.)
So ensure that there is only one solution, we will restrict the graph of y=sin(x) to the interval −π2≤x≤π2. This also guarantees that −1≤y≤1 as shown in Figure 2.33.
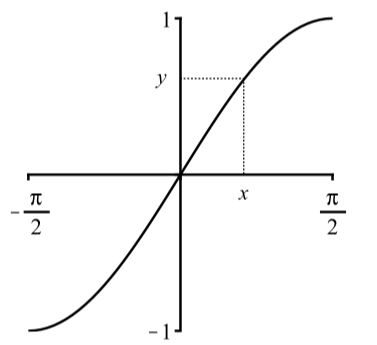
Figure 2.5.2: Graph of y=sin(x) restricted to −π2≤x≤π2
As is illustrated in Figure 2.5.2, for each value of y with −1≤y≤1, there is exactly one value of x with sin(x)=y and −π2≤x≤π2.
Definition
The inverse sine function (denoted by arcsin or sin−1), is defined as follows:
For −1≤y≤1, t=arcsin(y) or t=sin−1(y)
Caution. Either notation may be used for the arcsine function. That is, arcsin(y) and sin−1(y)) mean the same thing. However, the notation sin−1) does not mean the reciprocal of the sine but rather the inverse of the sine with a restricted domain. It is very important to remember the facts that the domain of the inverse sine is the interval [−1,1] and the range of the inverse sine is the interval [−π2,π2].
Note
Some people prefer using t=arcsin(y) instead of t=sin−1(y)) since it can be a reminder of what the notation means. The equation t=arcsin(y) is an abbreviation for t is the arc with sine value y and −π2≤x≤π2.
It is important to keep writing the restriction −π2≤x≤π2 since it is important to realize that arcsin(y) function gives only one arc whose sine value is y and t must be in this interval.
Example 2.5.1: Inverse Sine Function
We will determine the exact value of arcsin(√32). So we let t=arcsin(√32)
This means that sin(t)=√32
That is, we are trying to find the arc t whose sine is √32 and −π2≤y≤π2. Using our knowledge of sine values for common arcs, we notice that sin(π3)=√32 and so we conclude that t=π3 or that arcsin(√32)=π3
This is illustrated graphically in Figure 2.5.3.
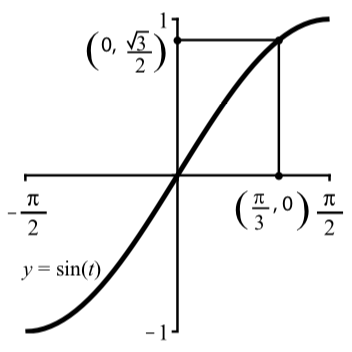
Figure 2.5.3: Graphical Version of arcsin(√32)=π3
Note: Most calculators and graphing utilities can calculate approximate values for the inverse sine function. On calculators, it is often the sin−1 key and for many computer programs, it is necessary to type “arcsin.” Using a calculator, we see that arcsin(√32)≈1.04720, which is a decimal approximation for π3.
Exercise 2.5.1
- arcsin(−√32)
- sin−1(12)
- arcsin(−1)
- arcsin(−√22)
In the next progress check, we will use the inverse sine function in two-step calculations. Please pay attention to the results that are obtained.
- Answer
-
1. arcsin(−√32)=−π3 since sin(−π3)=−√32 and −π2≤−π3≤π2.
2. sin−1(12)=π6 since sin(π2)=−12 and −π2≤π6≤π2.
3. arcsin(−1)=−π2 since sin(−π2)=−1 and −π2≤−π2≤π2.
4. arcsin(−√22)=−π4 since sin(−π4)=−√22 and −π2≤−π4≤π2.
Exercise 2.5.2
Determine the exact value of each of the following. You may check your results with a calculator.
- sin(sin−1(12))
- arcsin(sin(π4))
- sin(sin−1(12))
- arcsin(sin(3π4))
- Answer
-
1. Since sin−1(12)=π6, we see that sin(sin−1(12))=sin(π6)=12
2. arcsin(sin(π4))=arcsin(√22). In addition, arcsin(√22)=π4 since sin(π4)=√22 and −π2≤−π4≤π2. So we see that arcsin(sin(π4))=arcsin(√22)=π4.
3. We do not know an exact value for sin−1(25). So we let t=sin−1(25).
We then know that sin(t)=25 and −π2≤t≤π2.So
sin(sin−1(25))=sin(t)=25
4. arcsin(sin(π4))=arcsin(√22). In addition, arcsin(√22)=π4 since sin(π4)=√22 and −π2≤π4≤π2. So we see that arcsin(sin(π4))=arcsin(√22)=π4
The work in Exercise 2.5.2 illustrates some important properties of the inverse since function when it is composed with the sine function. This property is that in some sense, the inverse sine and the sine functions “undo” each other. To see what this means,we let y=sin(t) with −π2≤t≤π2. Then sin−1(sin(t))=sin−1(y)=t
Similarly, if t=sin−1(y) for some y with −1≤y≤1, then sin(sin−1(y))=sin(t)=y
Properties of the Inverse Sine Function
- For each t in the closed interval [−π2,π2], sin−1(sin(t))=t.
- For each y in the closed interval [−1,1], sin(sin−1(y))=y.
The Inverse Cosine and Inverse Tangent Functions
In a manner similar to how we defined the inverse sine function, we can define the inverse cosine and the inverse tangent functions. The key is to restrict the domain of the corresponding circular function so that we obtain the graph of a one-to-one function. So we will use y=cos(t) with 0≤t≤π and y=tan(t) with −π2<t<π2 as is illustrated in Figure 2.5.4.
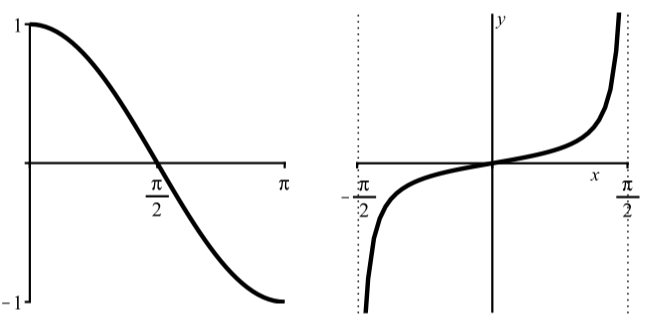
Figure 2.5.4: Graph of y=cos(t) for 0≤t≤π and Graph of y=tan(t) for −π2<t<π2.
Note
We do not use the interval −π2≤t≤π2 for the cosine function since the cosine function is not one-to-one on that interval. In addition, the interval for the tangent function does not contain the endpoints since the tangent function is not defined at and −π2 and π2.
Using these domains, we now define the inverse functions for cosine and tangent.
Definition
The inverse cosine function (denoted by arccos or cos−1), is defined as follows:
For −1≤y≤1, t=arccos(y) or t=cos−1(y)
We define the inverse tangent function (denoted by arctan or tan−1), as follows:
For t∈R, t=arctan(y) or t=tan−1(y)
Note
The preceding results can be written using the arcsine function rather than sin−1. It is very important to realize that these results are valid only for \(-\dfrac{\pi}{2} \leq x leq \dfrac{\pi}{2}\] and −1≤y≤1.
Example 2.5.2: An Example of Inverse Cosine
The equation y=arccos(−12)=cos−1(−12) means that cos(y)=−12 and 0≤y≤π.
That is, we are trying to find the arc y whose cosine is 0≤y≤π. Using our knowledge of cosine values for common arcs, we notice that cos(π3)=12. So we conclude that the reference angle ˆy for y is ˆy=π3. Since y must be in QII, we conclude that y=π−π3 or y=2π3. So arccos(−12)=2π3.
This can be checked using a calculator and is illustrated in Figure 2.5.5.
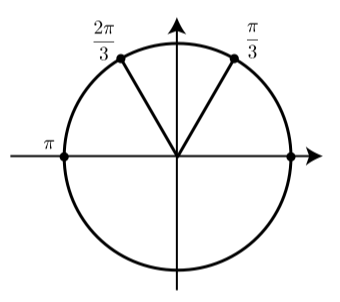
Figure 2.5.5: Diagram Used for the Inverse Cosine of −12.
Exercise 2.5.3
Determine the exact value of each of the following. You may check your results with a calculator.
- cos(cos−1(12))
- arccos(cos(π4))
- arccos(cos(−π4))
- tan−1(tan(5π4))
The work in Exercise 2.5.2 illustrates some important properties of the inverse cosine and inverse tangent functions similar to the properties of the inverse sine function on page 147.
- Answer
-
1. Since cos−1(12)=π3, we see that cos(cos−1(12))=cos(π3)=12.
2. arccos(cos(π4))=arccos(√22). In addition, arccos(√22)=π4 since cos(π4)=√22 and 0≤π4≤π. So we see that arccos(cos(π4))=arccos(√22)=π4.
3. arccos(cos(−π4))=arccos(√22). In addition, arccos(√22)=π4 since cos(π4)=√22 and 0≤3π4≤π. So we see that arccos(cos(−π4))=arccos(√22)=π4.
4. tan−1(tan(5π4))=tan−1(1). In addition, tan−1(1)=π4 since tan(π4)=1 and −π2≤π4≤π2. So we see that tan−1(tan(5π4))=tan−1(1)=π4
Properties of the Inverse Cosine Function
- For each t in the closed interval [0,π]: cos−1(cos(t))=t
- For each y in the closed interval [−1,1]: cos(cos−1(y))=y
Properties of the Inverse Tangent Function
- For each t in the open interval (−π2,π): tan−1(tan(t))=t
- For each real number y: tan(tan−1(y))=y
The justification for these properties is included in the exercises.
Exercise 2.5.4
Determine the exact value of each of the following and check them using a calculator.
- y=arccos(1)
- y=tan−1(√3)
- y=arctan(−1)
- y=cos−1(−√22)
- sin(arccos(−12))
- tan(arcsin(−√32))
- arccos(sin(π6))
When we evaluate an expression such as sin(arccos(−12)) in the previous preview activity, we can use the fact that it is possible to determine the exact value of arccos(−12) to complete the problem. If we are given a similar problem but do not know the exact value of an inverse trigonometric function, we can often use the Pythagorean Identity to help. We will do this in the next progress check.
- Answer
-
- y=arccos(1)=0
- y=tan(√3)=π3
- y=arctan(−1)=−π4
- y=cos−1(−√22)=3π4
- sin(arccos(12))=√32
- tan(arcsin(−√32))=−√3
- arccos(sin(π6))=π3
Exercise 2.5.5
- Determine the exact value of sin(arccos(13)). Following is a suggested way to start this. Since we do not know the exact value of arccos(13), we start by letting t=arccos(13). We then know that cos(t)=13 and 0≤t≤π. Notice that sin(t)=sin(arccos(13)). So to complete the problem, determine the exact value of sin(t) using the Pythagorean Identity keeping in mind that 0≤t≤π.
- Determine the exact value of cos(arcsin(−47))
- Answer
-
1. Let t=arccos(13). We then know that cos(t)=13 and 0≤t≤π
Using the Pythagorean Identity, we see that (13)2+sin2(t)=1 and this implies that sin2(t)=89. Since 0≤t≤π, t is in the second quadrant and in both of these quadrants, sin(t)>0. So, sin(t)=√83. That is, \[\sin(\arccos(\dfrac{1}{3})) = \dfrac{\sqrt{8}}{3}\).2. For cos(arcsin(−47)), we let t=arcsin(−47). This means that
sin(t)=−47 and −π2≤t≤π2.
We can use the Pythagorean Identity to obtain cos2(t)+(−47)2=1. This gives cos2(t)=3349. We also have the restriction −π2≤t≤π2 and we know sin(t)<0. This means that t must be in QIV and so cos(t)>0. Hence, cos(t)=√337. That is,cos(arcsin(−47))=√337
Note: You can use your calculator to check this work. Use your calculator to approximate both cos(arcsin(−47)) and √337. Both results should be 0.8206518066.
Summary
In this section, we studied the following important concepts and ideas:
- The Inverse Sine Function uniquely reverses what the sine function does. The inverse sine function takes a value y from the range of the sine function and gives us exactly one real number t whose sine is equal to y. That is, if y is a real number and −1≤y≤1, then sin−1(y)=t means that sin(t)=y and −π2≤x≤π2. In addition, the inverse sine function satisfies the following important properties:
- For each t in the closed interval [−π2,π2], sin−1(sin(t))=t
- For each y in the closed interval [−1,1], sin(sin−1(y))=y
- The Inverse cosine Function uniquely reverses what the cosine function does. The inverse cosine function takes a value y from the range of the cosine function and gives us exactly one real number t whose cosine is equal to y. That is, if y is a real number and −1≤y≤1, then cos−1(y)=t means that cos(t)=y and 0≤t≤π. In addition, the inverse cosine function satisfies the following important properties:
- For each t in the closed interval [0,π], cos−1(cos(t))=t
- For each y in the closed interval [−1,1], cos(cos−1(y))=y
- The Inverse Tangent Function uniquely reverses what the tangent function does. The inverse tangent function takes a value y from the range of the tangent function and gives us exactly one real number t whose tangent is equal to y. That is, if y is a real number, then tan−1(y)=t means that tan(t)=y and −π2<x<π2. In addition, the inverse tangent function satisfies the following important properties:
- For each t in the open interval (−π2,π2), tan−1(tan(t))=t
- For each real number y, tan(tan−1(y))=y


