2.6: Solving Trigonmetric Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
For these questions, we let q be a real number with −1≤q≤1 and let r be a real number.
- How can an inverse trigonometric function be used to determine one solution of an equation of the form sin(x)=q,cos(x)=q, or tan(x)=r?
- How can properties of the trigonometric functions be used to determine all solutions of an equation of the form sin(x)=q,cos(x)=q, or tan(x)=r? within one complete period of the trigonometric function?
- How can we use the period of a trigonometric function to determine a formula for the solutions of an equation of the form sin(x)=q,cos(x)=q, or tan(x)=r?
Recall that a mathematical equation like x2=1 is a relation between two expressions that may be true for some values of the variable while an identity like cos(−x)=cos(x) is an equation that is true for all allowable values of the variable. So an identity is a special type of equation. Equations that are not identities are also called conditional equations because they are not valid for all allowable values of the variable. To solve an equation means to find all of the values for the variables that make the two expressions on either side of the equation equal to each other. We solved algebraic equations in algebra and now we will solve trigonometric equations.
A trigonometric equation is an equation that involves trigonometric functions. We have already used graphical methods to approximate solutions of trigonometric equations. In Example 2.17, we used the function
V(t)=35cos(5π3t)+105
as a model for the amount of blood in the heart. For this function, t is measured in seconds since the heart was full and V .t / is measured in milliliters. To determine the times when there are 140 milliliters of blood in the heart, we needed to solve the equation
35cos(5π3t)+105=100
At that time, we used the “intersect” capability of a graphing utility to determine some solutions of this equation. In this section, we will learn how to use the inverse cosine function and properties of the cosine function to determine the solutions of this equation. We begin by first studying simpler equations.
Beginning Activity
Use a graphing utility to draw the graphs of y=cos(x) and y=0.7 on the same axes using −π≤x≤π and −1.2≤y≤1.2. Use the graphing utility to find the points of intersection of these two graphs and to determine solutions of the equation cos(x)=0.7
In the beginning activity, we should have determined the following approximations for solutions of the equation cos(x)=0.7:
- x1≈0.79540
- x1≈−0.79540
These approximations have been rounded to five decimal places.
The graph below shows the two graphs using −3π≤x≤3π. The solutions x1 and x2 are shown on the graph. As can be seen, the graph shows x1 and x2 and four other solutions to the equation cos(x)=0.7. In fact, if we imagine the graph extended indefinitely to the left and to the right, we can see that there are infinitely many solutions for this equation.
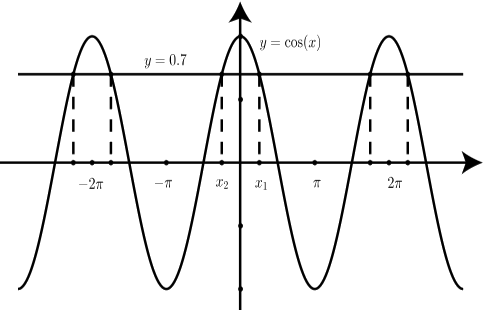
This is where we can use the fact that the period of the cosine function is 2π. The other solutions differ from x1 or x2 by an integer multiple of the period of 2π. We can represent an integer multiple of 2π by k(2π) for some integer k. So we say that any solution of the equation cos(x)=0.7 can be approximated by
x1≈0.79540+k(2π)
or
x1≈−0.79540+k(2π)
For example, if we use k=4, we see that x≈25.92814 or x≈24.33734.
We can use a calculator to check that for both values, cos(x)=0.7.
A Strategy for Solving a Trigonometric Equation
The example using the equation cos(x)=0.7 was designed to illustrate the fact that if there are no restrictions placed on the unknown x, then there can be infinitely many solutions for an equation of the form “some trigonometric function of x” = a number.
A general strategy to solve such equations is:
- Find all solutions of the equation within one period of the function. This is often done by using properties of the trigonometric function. Quite often, there will be two solutions within a single period.
- Use the period of the function to express formulas for all solutions by adding integer multiples of the period to each solution found in the first step. For example, if the function has a period of 2π and x1 and x2 are the only two solutions in a complete period, then we would write the solutions for the equation as x=x1+k(2π),x=x2+k(2π), where k is an integer.
Note
Instead of writing “k is an integer,” we could write k∈{⋯,−2,−1,0,1,2,⋯}.
Exercise 2.6.1
Use a graph to approximate the solutions (rounded to four decimal places) of the equation sin(x)=−0.6 on the interval −π≤x≤π. Then use the period of the sine function to write formulas that can be used to approximate any solution of this equation.
- Answer
-
Any solution of the equation sin(x)=−0.6 may be approximated with one of the following:
x≈0.64350+k(2π) or x≈2.49809+k(2π)
Using Inverse Functions to Solve Trigonometric Equations
Although we can use a graphing utility to determine approximations for solutions to many equations, we often need to have some notation to indicate specific numbers (that are often solutions of equations). We have already seen this in previous mathematics courses. For example, we use the notation √20 to represent the positive real number whose square is equal to 20. We can use this to say that the two solutions of the equation x2=20 are x=√20 and x=−√20
Notice that there are two solutions of the equation but √20 represents only one of those solutions. We will now learn how to use the inverse trigonometric functions to do something similar for trigonometric equations. One big difference is that most trigonometric equations will have infinitely many solutions instead of just two. We will use the inverse trigonometric functions to represent one solution of an equation and then learn how to represent all of the solutions in terms of this one solution. We will first show how this is done with the equation cos(x)=0.7 from the beginning activity for this section.
Example 2.6.1: Solving an Equation Involving the Cosine Function
For the equation cos(x)=0.7, we first use the result about the inverse cosine function on page 150, which states that for t in the closed interval [0,π], cos−1(cos(t))=t
So we “apply the inverse cosine function” to both sides of the equation cos(x)=0.7 This gives:
cos(x)=0.7
cos−1(cos(x))=cos−1(0.7)
x=cos−1(0.7)
Another thing we must remember is that this gives the one solution for the equation that is in interval [0,π]. Before we use the periodic property, we need to determine the other solutions for the equation in one complete period of the cosine function. We can use the interval [0,2π] but it is easier to use the interval [−π,π]. One reason for this is the following so-called “negative arc identity” stated on page 82.
\[\cos(-x) = \cos(x)\) for every real number x.
Hence, since one solution for the equation is x=cos−1(0.7), another solution is x=−cos−1(0.7). This means that the two solutions of the equation x=cos(x) on the interval [−π,π] are
x=cos−1(0.7) and x=−cos−1(0.7)
It can be verified that the equation cos(x)=0.7 has two solutions on the interval [−π,π] by drawing the graphs of y=cos(x) and y=0.7 on the interval [−π,π]. So if we restrict ourselves to this interval, we have something very much like solving the equation x2=20 in that there are two solutions that are negatives of each other. The main difference now is that the trigonometric equation has infinitely many solutions and as before, we now use the periodic property of the cosine function. Since the period is 2π, just like with the numerical approximations from the beginning activity, we can say that any solution of the equation cos(x)=0.7 will be of the form
x=cos−1(0.7)+k(2π) or x=−cos−1(0.7)+k(2π)
where k is some integer.
Exercise 2.6.2
Determine all solutions of the equation 4cos(x)+3=2 in the interval [−π,π]. Then use the periodic property of the cosine function to write formulas that can be used to generate all the solutions of this equation.
- Hint
-
First use algebra to rewrite the equation in the form cos(x) = “some number”.
- Answer
-
We first rewrite the equation 4cos(x)+3=2 as follows:
4cos(x)+3=24cos(x)=−1cos(x)=−14
So in the interval [−π,π], the solutions are x1=arccos(−14) and x2=−arccos(−14). So any solution of the equation 4cos(x)+3=2 is of the form
x=arccos(−14)+k(2π) or x=−arccos(−14)+k(2π)
The previous examples have shown that when using the inverse cosine function to solve equations of the form cos(x) = a number, it is easier to use the interval [−π,π]; rather than the interval [0,2π]. This is not necessarily true when using the inverse sine function since the inverse sine function gives a value in the interval [−π2,π2]. However, to keep things similar, we will continue to use the interval [−π,π]; as the complete period for the sine (or cosine) function. For the inverse sine, we use the following property stated on page 147.
For each t in the closed interval [−π2,π2], sin−1(sin(t))=t
When solving equations involving the cosine function, we also used a negative arc identity. We do the same and will use the following negative arc identity stated on page 82. sin(−x)=−sin(x) for every real number x.
Example 2.6.2: Solving an Equation Involving the Sine Function
We will illustrate the general process using the equation sin(x)=−0.6 from Progress Check 2.34. Because of the negative arc identity for the sine function, it is actually easier to work with the equation sin(x)=0.6. This is because if x=a is a solution of the equation sin(x)=0.6, then sin(−a)=−sin(a)=−0.6
and so, x=−a is a solution of the equation sin(x)=−0.6. For the equation sin(x)=0.6, we start by “applying the inverse sine function” to both sides of the equation.
sin(x)=0.6 sin−1(sin(x))=sin−1(0.6) x=sin−1(0.6)
We need to remember that this is only one solution of the equation. Since we know that the sine function is positive in the first and second quadrants, this solution is in the first quadrant and there is another solution in the second quadrant. Using x=sin−1(0.6) as a reference arc (angle), the solution in the second quadrant isx=π−sin−1(0.6). We now use the result that if x=a is a solution of the equation sin(x)=0.6, then x=−a is a solution of the equation sin(x)=−0.6. Please note that −(π−sin−1(0.6))=−π+sin−1(0.6)
Our work so far is summarized in the following table.
| Solutions for sin(x)=0.6 in [0,π] | Solutions for sin(x)=−0.6 in [−π,0] |
| x=sin−1(0.6) | x=−sin−1(0.6) |
| x=π−sin−1(0.6) | x=−π+sin−1(0.6) |
At this point, we should use a calculator to verify that the two values in the right column are actually solutions of the equation sin(x)=−0.6. Now that we have the solutions for sin(x)=−0.6 in one complete cycle, we can use the fact that the period of the sine function is 2π and say that the solutions of the equation sin(x)=−0.6 have the form
x=−sin−1(0.6)+k(2π) or x=(−π+sin−1(0.6))+k(2π)
where k is some integer.
Exercise 2.6.3
Determine all solutions of the equation 2sin(x)+1.2=2.5 in the interval [−π,π] Then use the periodic property of the sine function to write formulas that can be used to generate all the solutions of this equation.
Hint: First use algebra to rewrite the equation in the form sin(x) = “some number”.
- Answer
-
We first use algebra to rewrite the equation 2sin(x)+1.2=2.5 in the form
sin(x)=0.65
So in the interval [−π,π], the solutions are x1=arcsin(0.65) and x2=π−arcsin(0.65). So any solution of the equation 2sin(x)+1.2=2.5 is of the form
x=arcsin(0.65)+k(2π) or x=π−arcsin(0.65)+k(2π)
Solving More Complicated Trigonometric Equations
We have now learned to solve equations of the form cos(x)=q, and sin(x)=q, where q is a real number and −1≤q≤1. We can use our ability to solve these types of equations to help solve more complicated equations of the form cos(f(x))=q, and sin(f(x))=q where f is some function. The idea (which is typical in mathematics) is to convert this more complicated problem to two simpler problems. The idea is to:
- Make the substitution t=f(x) to get an equation of the form cos(t)=q, or sin(t)=q.
- Solve the equation in (1) for t.
- For each solution t of the equation in (1), solve the equation f(x)=t for x. This step may be easy, difficult, or perhaps impossible depending on the equation f(x)=t.
This process will be illustrated in the next progress check, which will be a guided investigation for solving the equation 3cos(2x+1)+6=5.
Exercise 2.6.4
We will solve the equation 3cos(2x+1)+6=5.
- First, use algebra to rewrite the equation in the form cos(2x+1)=−13. Then, make the substitution t=2x+1.
- Determine all solutions of the equation cos(t)=−13 with −π≤t≤π.
- For each of these two solutions, use t=2x+1 to find corresponding solutions for x. In addition, use the substitution t=2x+1 to write −π≤2x+1≤π and solve this inequality for x. This will give all of the solutions of the equation cos(2x+1)=−13 in one complete cycle of the function given by y=cos(2x+1)
- What is the period of the function y=cos(2x+1). Use the results in (3) and this period to write formulas that will generate all of the solutions of the equation cos(2x+1)=−13. These will be the solutions of the original equation 3cos(2x+1)+6=5.
- Answer
-
1. 3cos(2x+1)+6=5 3cos(2x+1)=−1 cos(2x+1)=−13
2. t=cos−1(−13) or t=−cos−1(−13).
3. 2x+1=cos−1(−13)
2x=cos−1(−13)−1
x=12cos−1(−13)−12
2x+1=−cos−1(−13)
2x=−cos−1(−13)−1
x=−12cos−1(−13)−12
4. The period of the function y=cos(2x+1). So the following formulas can be used to generate the solutions for the equation.
x=(12cos−1(−13)−12)+kπ or x=(−12cos−1(−13)−12)+kπ
where k is some integer. Notice that we added an integer multiple of the period, which is π, to the solutions in (3).
Solving Equations Involving the Tangent Function
Solving an equation of the form tan(x)=q is very similar to solving equations of the form cos(x)=q or sin(x)=q. The main differences are the tangent function has a period of π (instead of 2π), and the equation tan(x)=q has only one solution in a complete period. We, of course, use the inverse tangent function for the equation tan(x)=q.
Exercise 2.6.5
Use the inverse tangent function to determine one solution of the equation 4tan(x)+1=10 in the interval (−π2≤x≤π2). Then determine a formula that can be used to generate all solutions of this equation.
- Answer
-
We first write the equation 4tan(x)+1=10 in the form tan(x)=94. So the only solution of the equation in the interval −π2≤x≤π2 is
x=arctan(94)
Since the period of the tangent function is π, any solution of this equation can be written in the form x=arctan(94)+kπ where k is some integer.
Summary
A trigonometric equation is an equation that involves trigonometric functions. If we can write the trigonometric equation in the form “some trigonometric function of x” = a number, then we can use the following strategy to solve the equation.
- Find one solution of the equation using the appropriate inverse trigonometric function.
- Determine all solutions of the equation within one complete period of the trigonometric function. (This often involves the use of a reference arc based on the solution obtained in the first step.)
- Use the period of the function to write formulas for all of the solutions of the trigonometric equation.


