3.1: Transformations of f(x)

Last updated
Save as PDF

Page ID: 83121

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

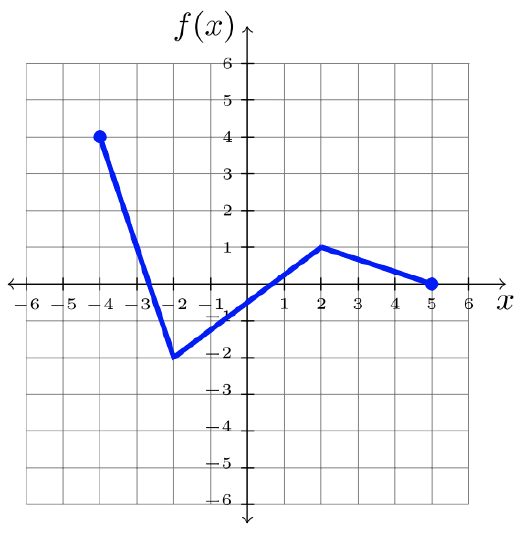
In this section, you will practice manipulating a given graph, according to the corresponding function notation. We’ll use the function $f$, graphed below, for demonstration throughout this section. But any graph will do!

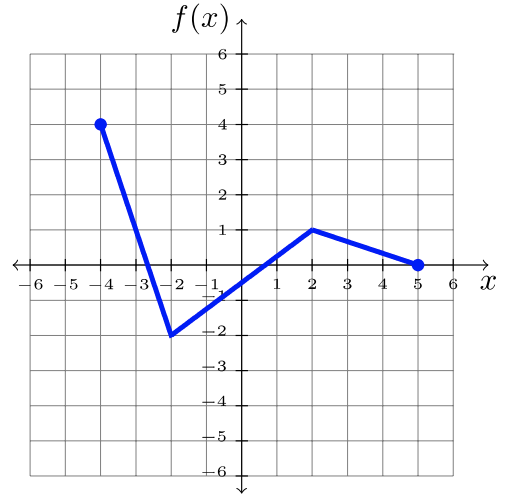
$clipboard_e875bf34ebe0dad0acc30e81768db0879.png$

By the end of this section, you’ll learn to read function notation like a blueprint, reposition the graph according to the instructions it gives. You will learn how to apply these transformations.

Transformation	Function Notation $(c > 0)$	Notes
Shift up $c$ units	0)\)">$0>y = f(x) + c$	If addition or subtraction is outside of the function, shift up or down.
Shift down $c$ units	0)\)">$0>y = f(x) − c$
Shift right $c$ units	0)\)">$0>y = f(x-c)$	If addition or subtraction is inside the function, shift left or right.
Shift left $c$ units	0)\)">$0>y = f(x+c)$
Reflection across the $x$-axis	0)\)">$0>y = -f(x)$	If the negative is outside of the function, there is an $x$-axis reflection.
Reflection across the $y$-axis	0)\)">$0>y=f(-x)$	If the negative is inside of the function, there is a $y$-axis reflection.
Vertical scale change	0)\)">$0>y=cf(x)$	If the multiplier, $c$, is outside of the function, there is a vertical scale change.
Horizontal scale change	0)\)">$0>y=f(cx)$	If the multiplier, $c$, is inside the function, there is a horizontal scale change.

The examples demonstrate the appropriate manipulation to the graph of $f$. The original graph $f$ is referred to as the parent graph. The concept can be applied to any function, but the same parent function is used in each example below.

Example 3.1.1

Using the graph of $f$, transform the graph appropriately.

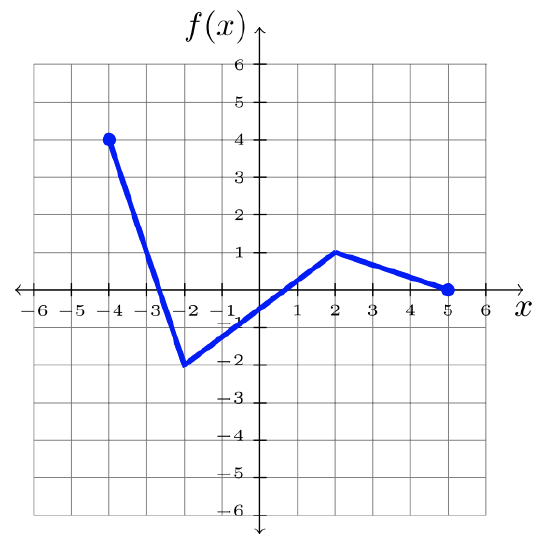
$clipboard_e2d2176d251eb10030c69df45e5cc1313.png$

$y = f(x + 2)$
$y = f(x) + 2$
$y = f(x − 2)$

Solution

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = f(x +2) &\text{Plus \(2$ Inside Function; Shift Left $2$} \end{array}\)

Step 2: Shift each point $2$ units left:

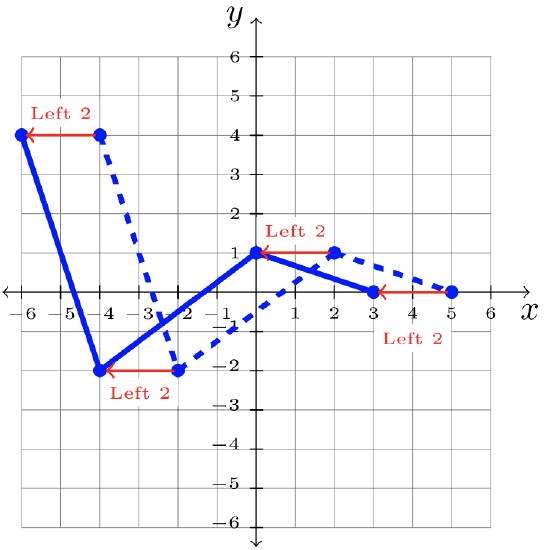
$clipboard_e469181cb9b243ed80c1b775f23085347.png$

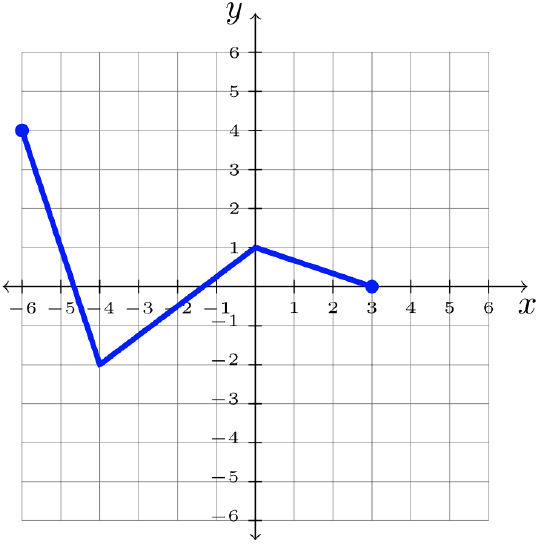
Step 3: Answer: $y = f(x + 2)$

$clipboard_e02f780464dea6cc0a1e4f0aedfbc29d8.png$

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = f(x) +2 &\text{Plus \(2$ Outside Function; Shift Up $2$} \end{array}\)

Step 2: Shift each point $2$ units up:

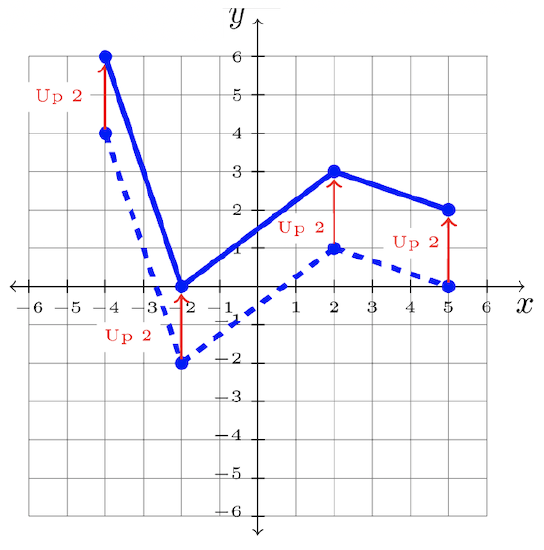
$clipboard_e73707b93dbc38fd9028329b78475e890.png$

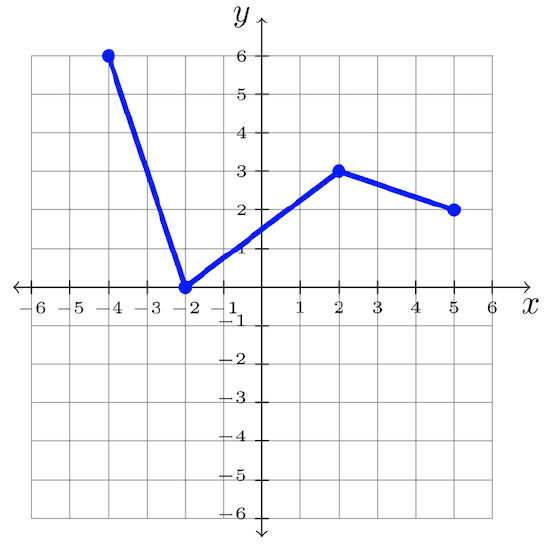
Step 3: Answer: $y = f(x )+ 2$

$clipboard_eb3fcac1d96da9c53ece8becd1d2bcc42.png$

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = f(x -2) &\text{Minus \(2$ Inside Function; Shift Right $2$} \end{array}\)

Step 2: Shift each point $2$ units right:

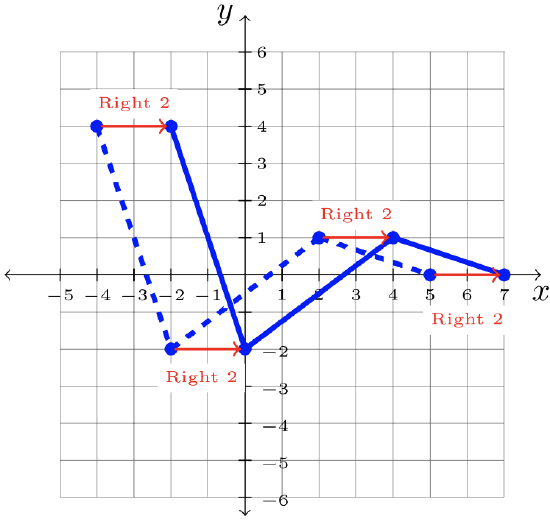
$clipboard_e71a3dc5f907fb95cd0d22fe990f50d63.png$

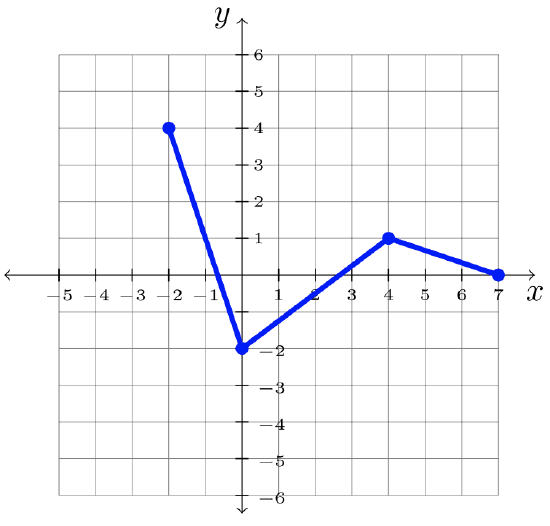
Step 3: Answer: $y = f(x -2)$

$clipboard_e1a05010f4575328b4795a0c62a54b25b.png$

Example 3.1.2

Using the graph of $f$, transform the graph appropriately.

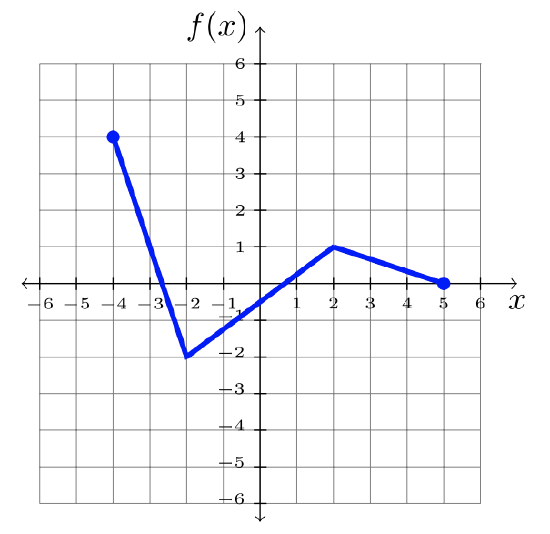
$clipboard_e9fac8dc7d5b6a747e28f8cc391c7696e.png$

$y = f(x) − 2$
$y = −f(x)$
$y = f(−x)$

Solution

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = f(x) -2 &\text{Minus \(2$ Outside Function; Shift Down $2$} \end{array}\)

Step 2: Shift each point $2$ units down:

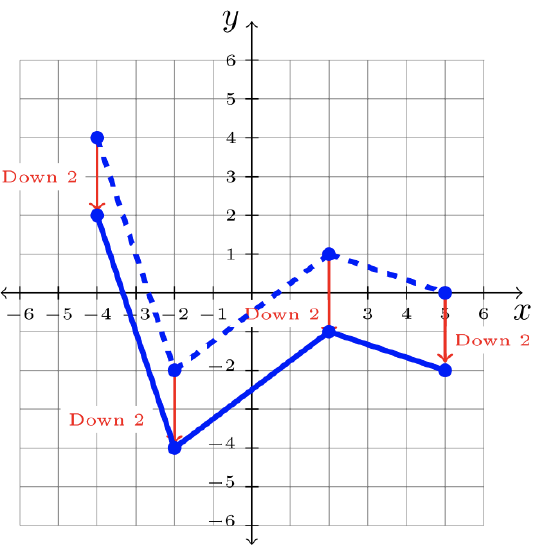
$clipboard_e1194024f492b8eaa2e6415a24f3788cb.png$

Step 3: Answer: $y = f(x) -2$

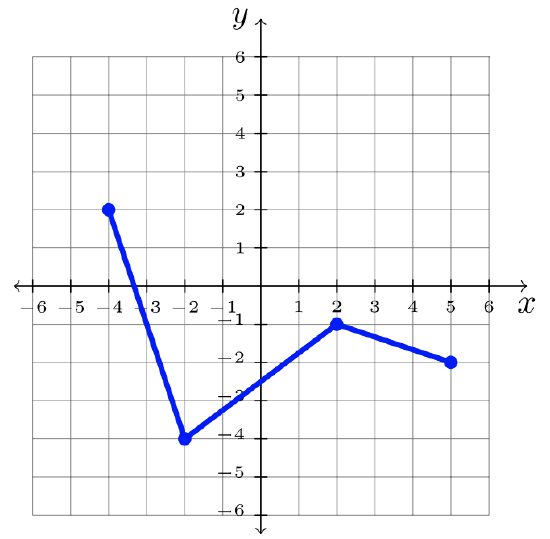
$clipboard_eb3d2cf4211427f995b6f394f5681a315.png$

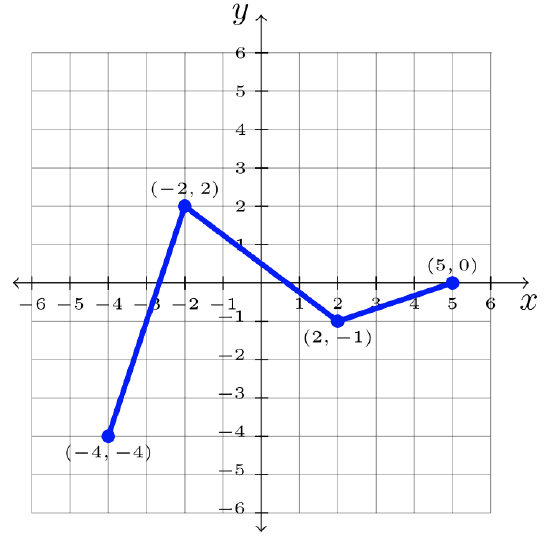
Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = -f(x) &\text{Negative Outside Function; \(x$-axis Reflection} \end{array}\)

Step 2: Change each $y$-value to its opposite.

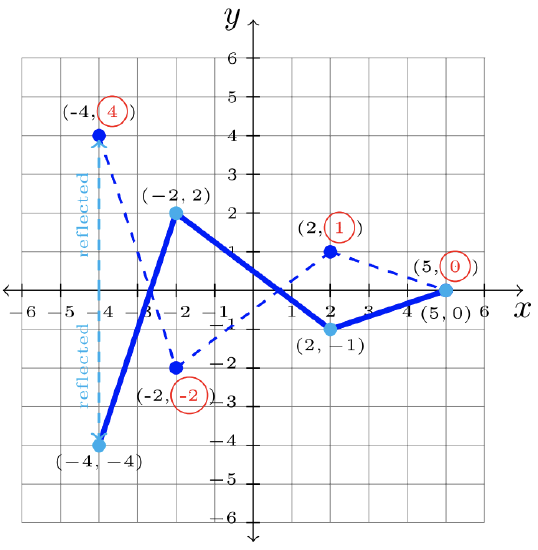
$clipboard_ee03ebc3c9f0770307d6bc6b7303da6e1.png$

Step 3: Answer: $y = −f(x)$

$clipboard_eabc1cb9829a80ec65ed116a4e0e246c4.png$

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = f(-x) &\text{Negative Inside Function; \(y$-axis Reflection} \end{array}\)

Step 2: Change each $x$-value to its opposite.

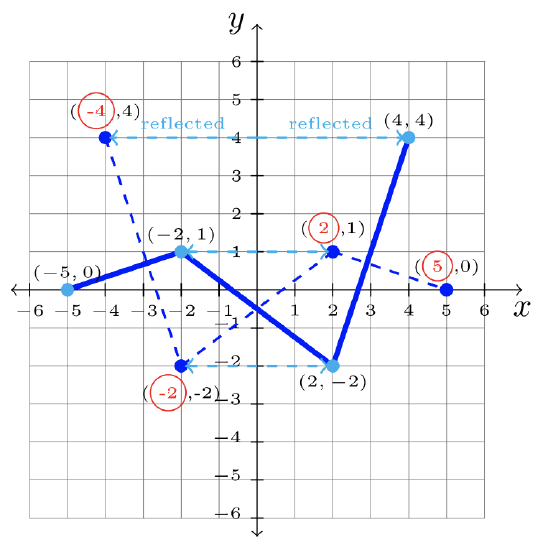
$clipboard_e16ec88e962438222d2253e27544fe4f8.png$

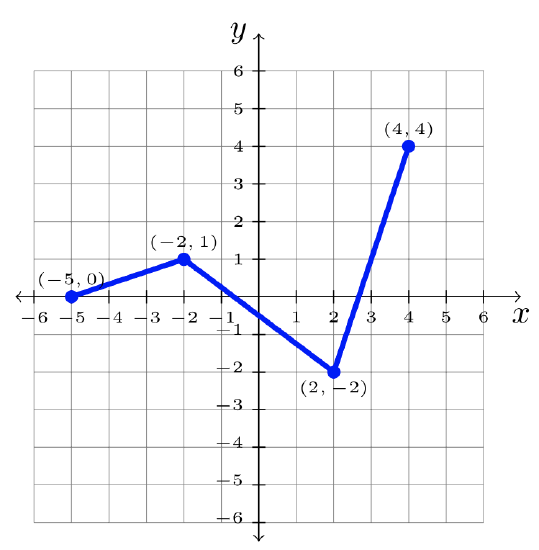
Step 3: Answer: $y = f(x) -2$:

$clipboard_ed5a33de0eaf6e5d5e04b95b2a2dbbf4c.png$

Example 3.1.3

Using the graph of $f$, transform the graph appropriately.

$clipboard_ecb192ed02cc8a953939287e033cdaa2b.png$

$y = 2f(x)$
$y = f(2x)$

Solution

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y = 2f(x) &\text{Times \(2$ Outside Function; Vertical Scale Change $2$} \end{array}\)

Step 2: Multiply each $y$-value by $2$.

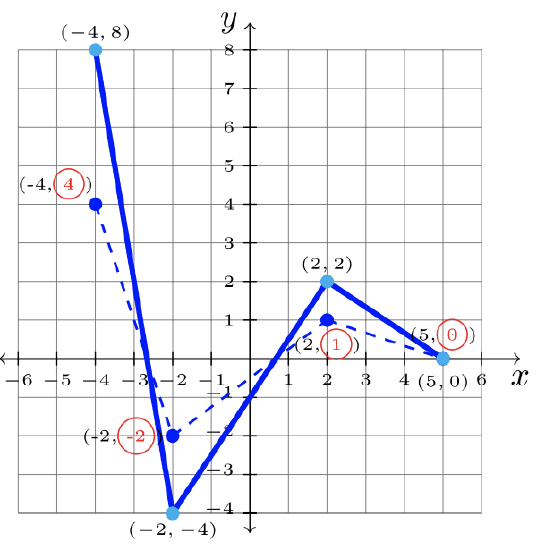
$clipboard_e00b176a7f0344043092b3c0ab8198244.png$

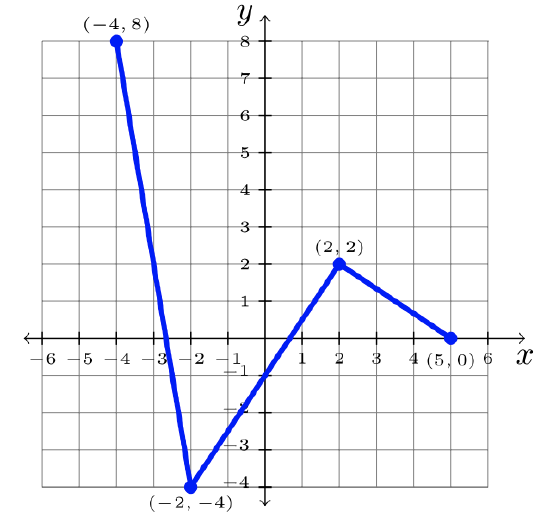
Step 3: Answer: $y = 2f(x)$:

$clipboard_e3ae4dd5ff56aa17a8792116e3c8213ca.png$

Caution: Horizontal scale change is counter-intuitive! For $y = f(cx)$, the graph of $f$ is scaled horizontally by a factor of $\dfrac{1}{c}$. In other words, if $c > 1$, then the graph is compressed. If $0 < c < 1$, (a proper fraction) then the graph is stretched horizontally

Step 1: Identify the transformation on the parent graph, $f$.

$\begin{array}&&y =- f(x) &\text{Minus \(2$ Outside Function; Shift Down $2$} \end{array}\)

Step 2: Multiply each $x$-value by $\dfrac{1}{2}$.

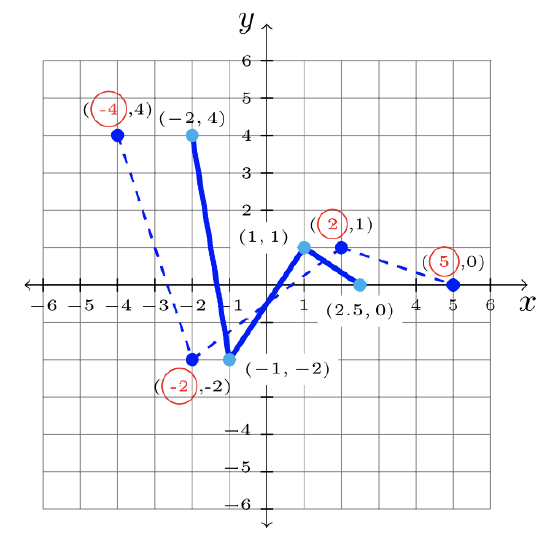
$clipboard_e8d13dafcd78e2a2a7f4340a3f13121c9.png$

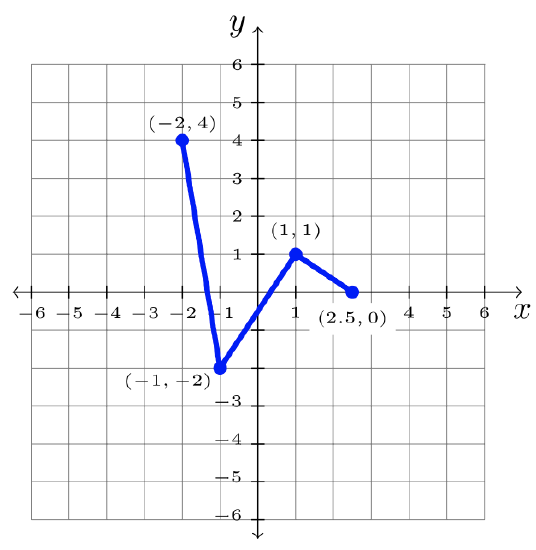
Step 3: Answer: $y = f(2x)$:

$clipboard_efb7600a4794e65743bd42843274c2a44.png$

Combining Transformations

In many cases, graphing a function will require more than one transformation. Perform transformations in the same order as PEMDAS, the order of operations. The next example demonstrates the manipulation of a graph using multiple transformations.

Example 3.1.4

Using the graph of $f$,

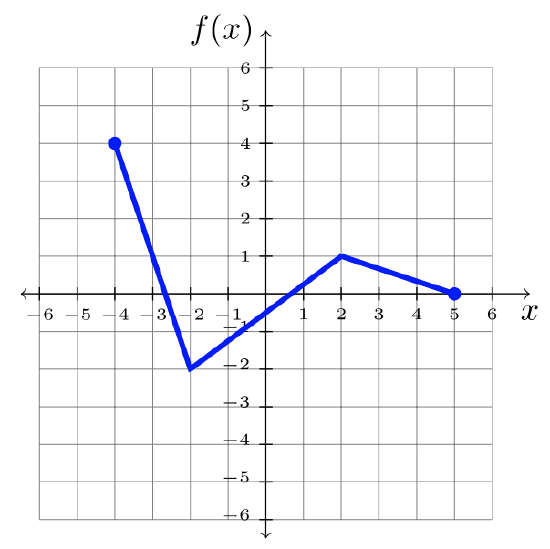
$clipboard_e7e61268272aa3bed562f306c2d133323.png$

Sketch the graph: $y = −2f(x − 1) − 3$

Solution

Since transformations are to be performed in the order of PEMDAS, each transformation is noted then ordered.

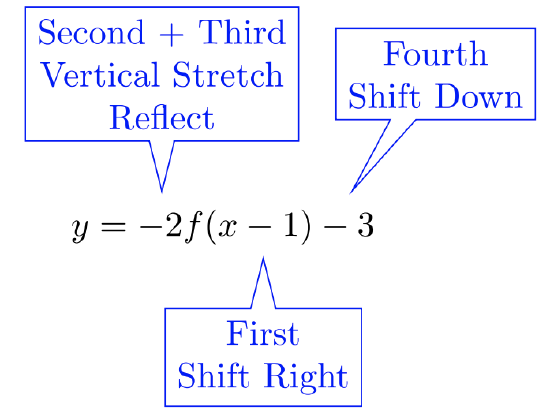
$clipboard_ebbea6b1e18ba21883c1f18463d0e790b.png$

The transformations of $4$ points of $f$ are charted below. After completing all transformations, plot the transformed points stated in the final column. Connect the points to create the graph.

$f$'s Point	Shift Right: Add one to each $x$-value.	Vertical Stretch & Reflect: Multiply $y$-values by $−2$.	Shift Down: Subtract $3$ from each $y$-value
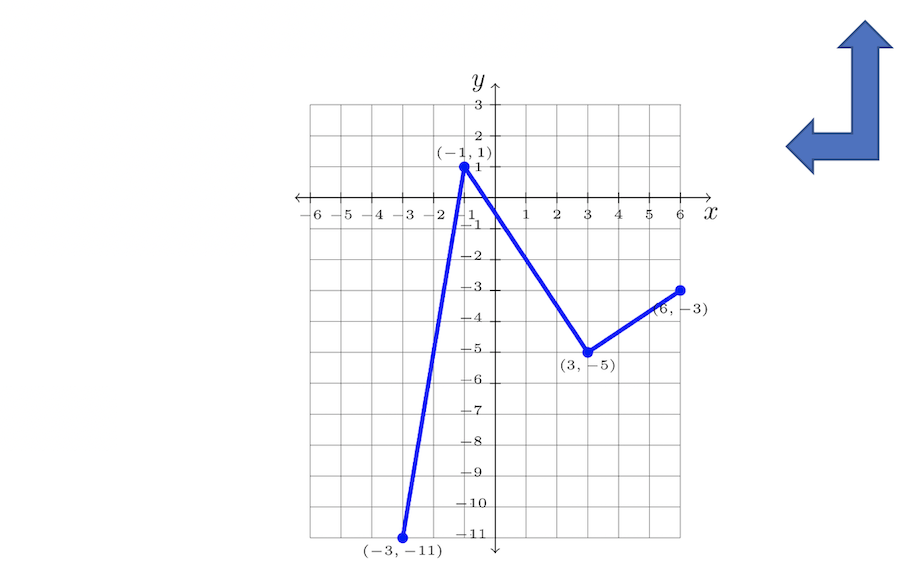
$(−4, 4)$	$(−3, 4)$	$(−3, −8)$	$(−3, −11)$
$(−2, −2)$	$(−1, −2)$	$(−1, 4)$	$(−1, 1)$
$ (2, 1)$	$(3, 1)$	$(3, −2)$	$(3,-5)$
$(5, 0)$	$(6, 0)$	$(6, 0)$	$(6,-3)$

The graph $y = −2f(x − 1) − 3$ is pictured below:

$clipboard_e6ac50ac078cf3c38dc4c641906dc6d85.png$

Try It! (Exercises)

For exercises 1-17, use the graph of $f$ at right, along with the appropriate transformation(s), to sketch the transformed function. Use graph paper.

$y = −f(x)$
$y = f(x) + 1$
$y = f(x + 2)$
$y = f(x − 3)$
$y = f(x) − 4$
$y = f(−x)$
$y = 3f(x)$
$y = f(2x)$
$y = \dfrac{1}{2} f(x)$
$y = f \left( \dfrac{1}{2} x \right)$
$y = −f(x)$
$y = 2f(x + 1)$
$y = 4 + f(x − 2)$
$y = 3 − f(x)$
$y = f(x − 3) − 3$
$y = −3f \left( \dfrac{1}{3} x \right)$
$y = 2f(−x) − 1$

For #18-24, write the function that would correspond to the described transformations on $f$.

Reflect $f$ through the $y$-axis, then move the graph up $5$ units.
Stretch $f$ vertically by a factor of $6$, then shift the graph left $8$ units.
Shift the graph of $f$ to the right $10$ units, then shift the graph down $7$ units.
Reflect $f$ through the $x$-axis, move the graph $3$ units right, then shift the graph up $12$ units.
Reflect $f$ through the $x$-axis, stretch it vertically by a factor of $4$, then shift it down $5$ units.
Reflect $f$ through the $y$-axis, shift it left (9\) units, then shift it up $8$ units.
Compress $f$ horizontally by a factor of $\dfrac{1}{4}$, reflect it through the $x$-axis, then shift down $1$ unit.

Transformation	Function Notation \((c > 0)\)	Notes
Shift up \(c\) units	0)\)">\(0>y = f(x) + c\)	If addition or subtraction is outside of the function, shift up or down.
Shift down \(c\) units	0)\)">\(0>y = f(x) − c\)
Shift right \(c\) units	0)\)">\(0>y = f(x-c)\)	If addition or subtraction is inside the function, shift left or right.
Shift left \(c\) units	0)\)">\(0>y = f(x+c)\)
Reflection across the \(x\)-axis	0)\)">\(0>y = -f(x)\)	If the negative is outside of the function, there is an \(x\)-axis reflection.
Reflection across the \(y\)-axis	0)\)">\(0>y=f(-x)\)	If the negative is inside of the function, there is a \(y\)-axis reflection.
Vertical scale change	0)\)">\(0>y=cf(x)\)	If the multiplier, \(c\), is outside of the function, there is a vertical scale change.
Horizontal scale change	0)\)">\(0>y=f(cx)\)	If the multiplier, \(c\), is inside the function, there is a horizontal scale change.

\(f\)'s Point	Shift Right: Add one to each \(x\)-value.	Vertical Stretch & Reflect: Multiply \(y\)-values by \(−2\).	Shift Down: Subtract \(3\) from each \(y\)-value
\((−4, 4)\)	\((−3, 4)\)	\((−3, −8)\)	\((−3, −11)\)
\((−2, −2)\)	\((−1, −2)\)	\((−1, 4)\)	\((−1, 1)\)
\( (2, 1)\)	\((3, 1)\)	\((3, −2)\)	\((3,-5)\)
\((5, 0)\)	\((6, 0)\)	\((6, 0)\)	\((6,-3)\)