4.2: Interval Notation

Last updated
Save as PDF

Page ID: 83128

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Inequalities slice and dice the real number line into segments of interest or intervals. An interval is a continuous, uninterrupted subset of real numbers. How can we notate intervals with simplicity? The table below introduces Interval Notation.

Inequality	Associated Circle	Associated Endpoint Closures
Either $<$ or $>$	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	Left Parenthesis: ( or Right Parenthesis: )
Either $≤$ or $≥$	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	Left Square bracket: [ or Right Square Bracket: ]

Inequalities have $4$ possible interval closures:

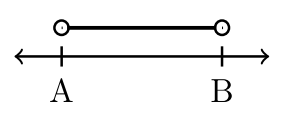
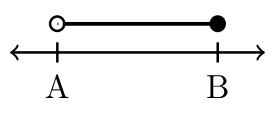
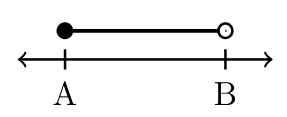
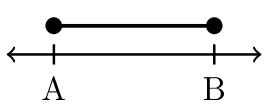
$(A,B)$	$(A,B]$	$[A,B)$	$[A,B]$
$clipboard_ef4d418cfbf59895619f0546ad98eaf4f.png$	$clipboard_e510d65b9070b6f966181489fb9235b67.png$	$clipboard_edce393fed1ea667df1f70b28c7dbb00e.png$	$clipboard_e9bbd934e732ad52963b83f2dac9d6bed.png$

The least number in the interval, $A$, is always stated first. A comma is placed. The largest number in the interval, $B$, is stated after the comma. The appropriate closure is considered for each value $A$ and $B$.

Four Examples of Interval Notation

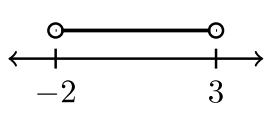
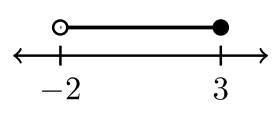
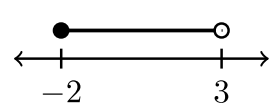
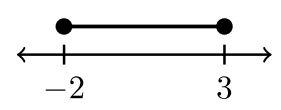
$−2 < x < 3$	$−2 < x ≤ 3$	$– 2 ≤ x < 3$	$– 2 ≤ x ≤ 3$
$clipboard_eb02fe1b987d2d7aeb60c8fea96ed2803.png$	$clipboard_e019534632b13aa8f1cc8d1d9d3d569d9.png$	$clipboard_edea90ab320a9712b9de1bd8371585e1b.png$	$clipboard_e8b9543e4ca42fb42ac9e7d44a55396c3.png$
$(−2, 3)$	$(−2, 3]$	$[−2, 3)$	$[−2, 3]$

The Infinities

There are two infinities: positive and negative. Each define a direction on the number line:

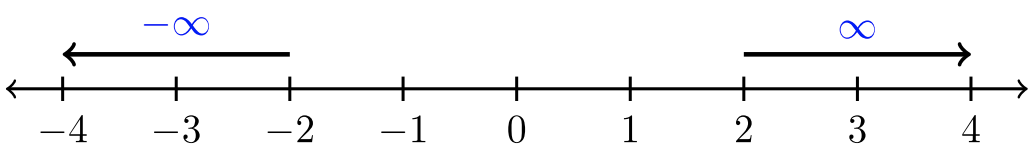
$clipboard_e5b29aa7ac89e2b9ce0b9a83ff14aa23a.png$

Infinity is not a real number. It indicates a direction. Therefore, when using interval notation, always enclose $∞$ and $−∞$ with parenthesis. We never enclose infinities with square bracket.

The table below shows four examples of interval notation that require the use of infinity.

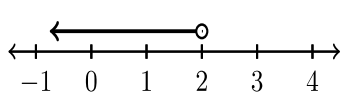
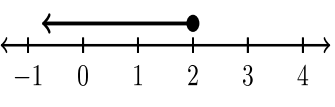
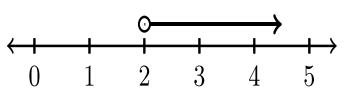
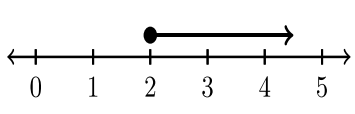
$x < 2$	$x ≤ 2$	$x > 2$	$x ≥ 2$
$clipboard_e5734c942cda8d2c4a2fc66d380d43045.png$	$clipboard_e02fd4cce2c4fdbda973bec7ec7cea27d.png$	$clipboard_eaf1970b524b0ed982616d4f351aef523.png$	$clipboard_ed53713ef79ac5f76e978d135bba630af.png$
$(−∞, 2)$	$(−∞, 2]$	$(2, ∞)$	$[2, ∞)$

Combinations of Intervals

If two or more intervals are interrupted with a gap in the number line, set notation is used to stitch the intervals together, symbolically. The symbol we use to combine intervals is the union symbol: $∪$. The table below shows four examples:

Interval Notation	Graph
$(−∞, −2) ∪ [1, ∞)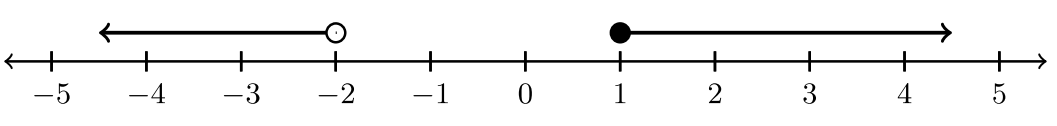$	$clipboard_ee59da9758674b8fbf6ec2276685e5423.png$
$(−∞, −1) ∪ (−1, ∞)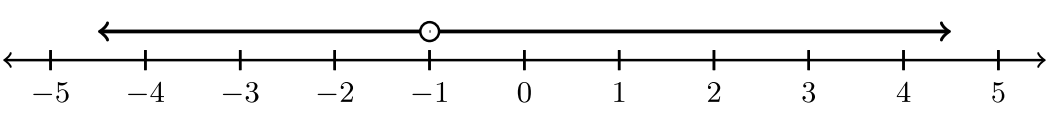$	$clipboard_ed827350d30be0e842f3deae80c6892f7.png$
$\left(−\dfrac{3 \pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left( \dfrac{\pi}{2}, \dfrac{3 \pi}{2} \right)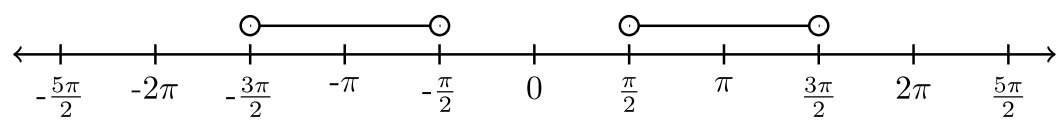$	$clipboard_ebbcf3adffba82a210520564b5a4782e1.png$
$\left[−2 \pi, − \dfrac{\pi}{2} \right) ∪ \left[ \dfrac{3 \pi}{2} , ∞ \right)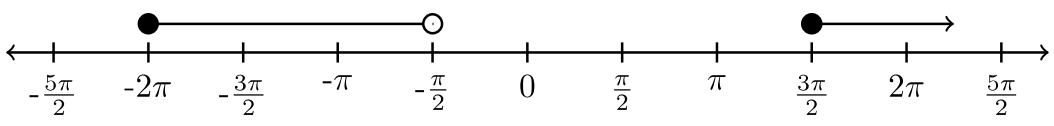$	$clipboard_ef225c28a7a5773a54ade751969064732.png$

Compound Inequalities

Intervals that have gaps, like the ones shown above, translate to compound inequalities. Real solutions belong in one interval or another. The word “or” plays a key role when translating. For example: the interval $(−∞, −2) ∪ [1, ∞)$ translates to its associated compound inequality:

$x < -2$ or $x ≥ 1$

The word “and” cannot be used between the inequalities because a number cannot belong to both intervals at once. For example, $x = 5$ is a solution because $5$ belongs in the interval $x ≥ 1$, but $5$ does not belong in the interval $x < −2$. Nevertheless, because of the word “or,” $x = 5$ is a solution to the interval $(−∞, −2) ∪ [1, ∞)$.

Try It! (Exercises)

For exercises #1-6, state the inequality and the interval notation associated with the graph.

Graph			Inequality	Interval Notation
$clipboard_e141ee93db0e0b1fcece04011d50b027c.png$
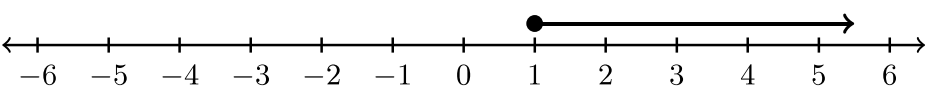$clipboard_ee998ec64608d5197c3eb0225a8dabfb4.png$
$clipboard_e387a79a4c9d9a3c5536f90ca06cc706a.png$
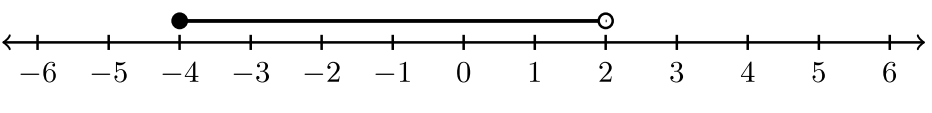$clipboard_e520b9807a5ebbd773c86cc029f9dd4cd.png$
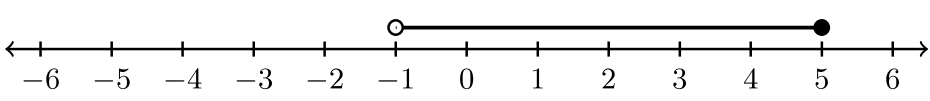$clipboard_e90ef48553dcc2b631e06459ee8b7d36b.png$
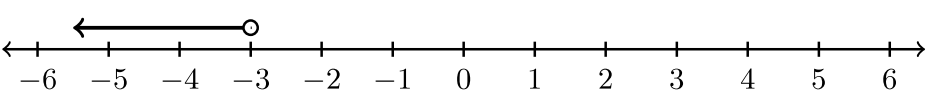$clipboard_e82c969b77994d0dd174ccb04a54f7dec.png$

For exercises #7-10, state the interval notation and sketch the graph associated with the inequality.

Graph			Inequality	Interval Notation
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$−3 ≤ x ≤ 1$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x < 4$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x ≥ −2$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$0 ≤ x < 3$

For exercises #11-17, sketch the graph associated with the given interval notation.

Graph			Interval Notation
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, 4)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −3) ∪ [0, ∞)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$[−1, 1) ∪ [2, ∞)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −5] ∪ (−1, 5)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left[−\dfrac{\pi}{2} , \dfrac{\pi}{2} \right]$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$(−∞, −\pi] ∪ [\pi, ∞)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left(−\dfrac{3\pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left(-\dfrac{\pi}{2} , 0\right)$

For #18-21

a. Sketch a graph of the compound inequality.

b. State the interval using interval notation.

$x ≥ 4$ or $x ≤ 0$
$x ≤ – 2\pi$ or $x > \pi$
$−1 > x$ or $2 ≤ x$
$x > 3\pi$ or $x < – \pi$

\(−2 < x < 3\)	\(−2 < x ≤ 3\)	\(– 2 ≤ x < 3\)	\(– 2 ≤ x ≤ 3\)
$clipboard_eb02fe1b987d2d7aeb60c8fea96ed2803.png$	$clipboard_e019534632b13aa8f1cc8d1d9d3d569d9.png$	$clipboard_edea90ab320a9712b9de1bd8371585e1b.png$	$clipboard_e8b9543e4ca42fb42ac9e7d44a55396c3.png$
\((−2, 3)\)	\((−2, 3]\)	\([−2, 3)\)	\([−2, 3]\)

\(x < 2\)	\(x ≤ 2\)	\(x > 2\)	\(x ≥ 2\)
$clipboard_e5734c942cda8d2c4a2fc66d380d43045.png$	$clipboard_e02fd4cce2c4fdbda973bec7ec7cea27d.png$	$clipboard_eaf1970b524b0ed982616d4f351aef523.png$	$clipboard_ed53713ef79ac5f76e978d135bba630af.png$
\((−∞, 2)\)	\((−∞, 2]\)	\((2, ∞)\)	\([2, ∞)\)

Inequality	Associated Circle	Associated Endpoint Closures
Either \(<\) or \(>\)	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	Left Parenthesis: ( or Right Parenthesis: )
Either \(≤\) or \(≥\)	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	Left Square bracket: [ or Right Square Bracket: ]

\((A,B)\)	\((A,B]\)	\([A,B)\)	\([A,B]\)
$clipboard_ef4d418cfbf59895619f0546ad98eaf4f.png$	$clipboard_e510d65b9070b6f966181489fb9235b67.png$	$clipboard_edce393fed1ea667df1f70b28c7dbb00e.png$	$clipboard_e9bbd934e732ad52963b83f2dac9d6bed.png$

Interval Notation	Graph
\((−∞, −2) ∪ [1, ∞)\)	$clipboard_ee59da9758674b8fbf6ec2276685e5423.png$
\((−∞, −1) ∪ (−1, ∞)\)	$clipboard_ed827350d30be0e842f3deae80c6892f7.png$
\(\left(−\dfrac{3 \pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left( \dfrac{\pi}{2}, \dfrac{3 \pi}{2} \right)\)	$clipboard_ebbcf3adffba82a210520564b5a4782e1.png$
\(\left[−2 \pi, − \dfrac{\pi}{2} \right) ∪ \left[ \dfrac{3 \pi}{2} , ∞ \right)\)	$clipboard_ef225c28a7a5773a54ade751969064732.png$

Graph			Inequality	Interval Notation
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(−3 ≤ x ≤ 1\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(x < 4\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(x ≥ −2\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(0 ≤ x < 3\)

Graph			Interval Notation
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, 4)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, −3) ∪ [0, ∞)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\([−1, 1) ∪ [2, ∞)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, −5] ∪ (−1, 5)\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\(\left[−\dfrac{\pi}{2} , \dfrac{\pi}{2} \right]\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\((−∞, −\pi] ∪ [\pi, ∞)\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\(\left(−\dfrac{3\pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left(-\dfrac{\pi}{2} , 0\right)\)