4.3: Solving Linear Inequalities

Last updated
Save as PDF

Page ID: 83130

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Linear equations have just one solution. Linear inequalities have infinitely many solutions, requiring intervals to express solutions. Let’s compare:

Linear Equation	Linear Inequality
$\begin{array} &4b − 3 &= 5 \\ 4b − 3 + 3 &= 5 + 3 \\ 4b &= 8 \\ b &= 2 \end{array}$	$\begin{array} &4b − 3 &> 5 \\ 4b − 3 + 3 &> 5 + 3 \\ 4b &> 8 \\ b &> 2 \end{array}$
Solutions set: $b = \{2\}$	Solution set: $\{b\| b > 2\}$ or Interval $(2, ∞)$

Set-builder Notation: To express solutions using set notation, the curly-brackets are used.

The condition of the set is descriptive. The inequality describes the condition. A number must meet the condition to qualify as a solution.

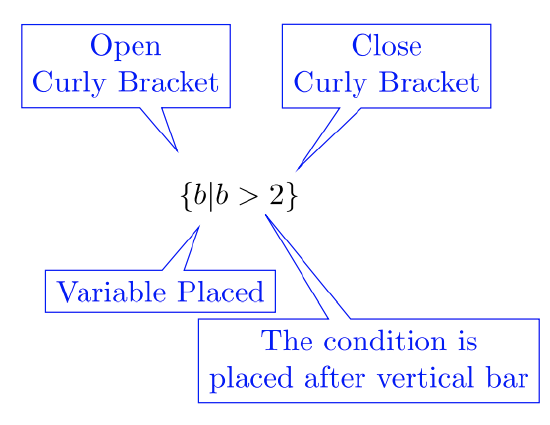
$clipboard_ef507e48df12b614acfb098c9f4dc7db6.png$

In this case, all numbers larger than two qualify as solutions, and those numbers belong to the solution set.

Note

Although addition and subtraction properties of inequality are the same for inequalities as they are for equalities, multiplication and division properties differ when multiplying or dividing by a negative. Dividing or multiplying both sides of an inequality by a negative reverses the inequality sign.

Example 4.3.1

Solve the inequality and graph the solution set. State the answer in both set builder notation and in interval notation.

$−6x − 5 ≥ 13$

Solution

$\begin{array} &&-6x-5 \geq 13 &\text{Add \(5$ to each side} \\ &-6x \geq 18 &\\ &\dfrac{-6x}{-6} \leq \dfrac{18}{-6}&\text{Dividing by a negative reverses the inequality} \\ &x \leq -3& \end{array}\)

Answers:

Set Builder Notation: $\{x| x ≤ −3\}$

Interval Notation: $(−∞, −3]$

Graph:

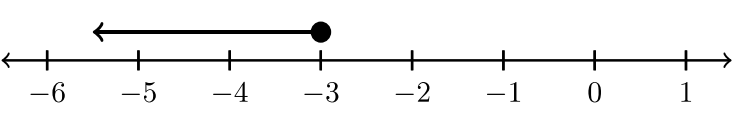
$clipboard_e493e50182b04651283bf373fb5a7a0a7.png$

Example 4.3.2

Solve the inequality and graph the solution set. State the answer in both set builder notation and in interval notation.

$10 − (2y + 1) ≤ −4(3y + 2) − 3$

Solution

Stay vigilant for any step in the solution where you multiply both sides by a negative or divide both sides by a negative. Otherwise, solve the inequality in the same manner you solve equalities.

$\begin{array} & &10 − 2y − 1 ≤ −12y − 8 − 3 &\text{Simplify each side by clearing parentheses.}\\ & −2y+ 9 ≤ −12y − 11 &\text{Simplify each side by combining like terms.}\\ & −2y + 12y + 9 ≤ −12y + 12y + (−11)&\text{Add \(12y$ to both sides. }\\ &10y + 9 ≤ −11 &\text{Simplify by combining like terms.}\\ &10y + 9 − 9 ≤ −11 − 9 &\text{Subtract $9$ to both sides.}\\ &10y ≤ −20 &\text{Simplify}\\ &\left. \begin{array}{ll} \dfrac{10y}{10} \leq -\dfrac{20}{10}\\ \;\;y \leq -2 \end{array} \right\} \text{ Dividing by a positive} &\text{The inequality is not reversed.} \end{array}\)

Answers:

Set Builder Notation: $\{y| y ≤ −2\}$

Interval Notation: $(−∞, −2]$

Graph:

$clipboard_e32d3225eb7fd1da855eeaa0fcaf17bc6.png$

Taking Different Steps Should Lead to the Same Answer

In many cases, arriving at an answer can come from different paths! No matter the path, if the math performed along the way is sound, the answer should be the same.

Example 4.3.3

Solve the inequality for $w$: $6w − 7 < 9w + 5$

Solution

$\begin{array} &&\text{Method #}1 && \text{Method #}2 \\ &6w − 7 < 9w + 5 && 6w − 7 < 9w + 5 \\
&6w − 6q − 7 < 9q − 6q + 5 &\textcolor{red}{\longleftarrow\text{Compare these steps!}\longrightarrow} & 6w − 9w − 7 < 9w − 9w + 5 \\ &−7 < 3w + 5 && −3w − 7 < 5 \\ &−7 − 5 < 3w + 5 − 5 && −3w − 7 + 7 < 5 + 7 \\ &−12 < 3w && −3w < 12 \\ &\dfrac{-12}{3} < \dfrac{3w}{3} &\textcolor{red}{\longleftarrow\text{Compare these steps!}\longrightarrow}& \dfrac{-3w}{-3} > \dfrac{12}{-3} \\ &−4 < w &\;\;\text{The answers are the same!} & w > −4 \end{array}$

Try It! (Exercises)

For each of the exercises #1-20,

Solve the inequality for the variable indicated.
Express the solution set in both set-builder notation and in interval notation.
Graph the solution set.

$−2p < 10$
$−9 < 3y$
$16 ≤ 5t + 1$
$−14 ≥ 4x + 2$
$6y − 10 > 4y$
$8b + 3 < 7b − 1$
$−2a − 3 ≤ 4a + 3$
$9 − u ≤ 11 + u$
$7 − 5p ≥ 8 − 10p$
$5(v + 1) > 3(y − 1)$
$2(11 − 3t) < 4(t − 2)$
$6(4y − 3) ≤ −3(6 − 7y)$
$8a − (6 + 2a) ≥ 3(4a − 6)$
$10 − 2(7 + x) > 7 − 3(3x − 1)$
$3 + 5(3 − 2d) ≤ 18 − 6(4d − 7)$
$7p− (10 − 25p) > 4p − 9(4p − 6)$
$\dfrac{1}{2}x − \dfrac{3}{4} < x + \dfrac{1}{4}$
$\dfrac{3}{5} (y + 5) > \dfrac{2}{5} (y − 10)$
$\dfrac{1}{6} (q − 2) ≤ \dfrac{1}{3} (q + 2)$
$1 − \dfrac{1}{4} (2t − 1) ≥ \dfrac{3}{4} + \dfrac{1}{2} (t + 1)$

Linear Equation	Linear Inequality
\(\begin{array} &4b − 3 &= 5 \\ 4b − 3 + 3 &= 5 + 3 \\ 4b &= 8 \\ b &= 2 \end{array}\)	\(\begin{array} &4b − 3 &> 5 \\ 4b − 3 + 3 &> 5 + 3 \\ 4b &> 8 \\ b &> 2 \end{array}\)
Solutions set: \(b = \{2\}\)	Solution set: \(\{b\| b > 2\}\) or Interval \((2, ∞)\)