4.4: Absolute Value Equations and Inequalities as Applied to Distance

Last updated
Save as PDF

Page ID: 83132

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The absolute value function, denoted $y=|x|$, takes any negative real number input and outputs the positive version of that number. Nonnegative numbers are left unchanged. Here’s a few examples:

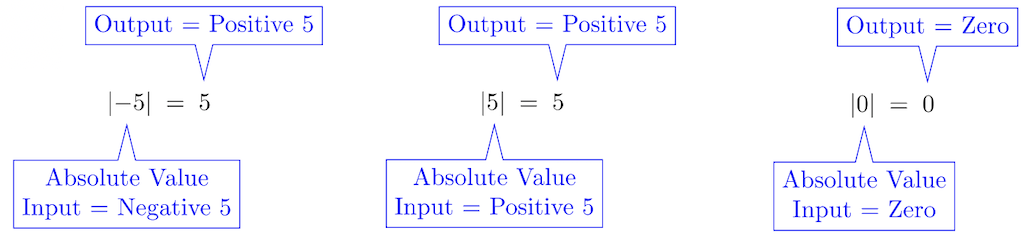
$clipboard_e6c7e1a344033657c2988c6a555298bc2.png$

Measuring distance is a good application to demonstrate the usefulness of this function. Distance is never negative. In fact, let’s view the absolute value function through the lens of measuring distance to better understand absolute value equations and inequalities:

Geometric Definition of the Absolute Value of a Real Number

The absolute value of a real number $b$, denoted $|b|$, is the distance between zero and $b$ on the number line.

The above examples can be geometrically interpreted by this graph:

$clipboard_e860d48e41f585c8daf81ed3862fd3345.png$

Example 4.4.1

Solve for $x$: $|x| = 3$.

Solution

What numbers are a distance of $3$ units from zero? A number line graph tells us! Both $3$ and $-3$ are a distance of $3$ units from zero.

Answer $x = \{−3, 3\}$

The Distance Between a and b

Absolute value is often used to measure the distance between two numbers, $a$ and $b$. If we use absolute value bars around the subtracted quantity, then the order of subtraction does not matter.

Distance From a to b

The distance from $a$ to $b$ is the absolute value of the difference.

$|a-b| = |b-a| = \text{distance between } a \text{ and } b$

Draw a number line and practice finding the distance between any two points. Convince yourself that the above formula works!

Example 4.4.2

Solve for $x$: $|x-3| = 4$

Use the geometric concept of distance to show solution.

Solution

Let’s break down the equation into meaningful words:

$\overbrace{|x-3|}^{\text{distance from } x \text{ to } 3} \overbrace{=}^{\text{is}} 4: “\text{The distance from the number \(3$ to another number $x$ is $4$ units.}”\)

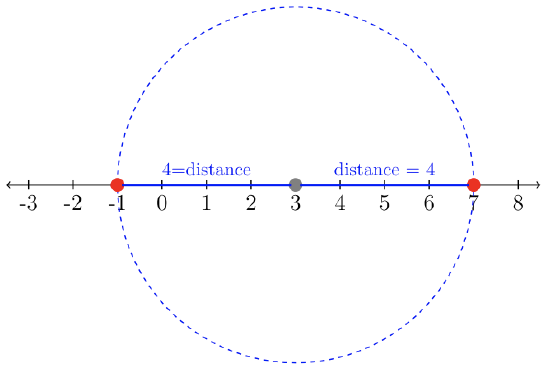
$clipboard_e4f1a30adcc425e61e0b304401792dca8.png$

It’s quite effective to think of the value $3$ as the center of a circle of radius $4$. The circle crosses the number line, marking the distance of $4$ units in each direction. The visual tells us the two answers are $−1$ and $7$.

Answer $x = \{−1, 7\}$

$\textcolor{green}{\checkmark}$ Confirm the visual solution matches the math:

$\begin{array} &\text{Let } x = −1 &&\;\;\;\;\;\;\;\;\;\;\;\;\;\text{Let } x = 7 \\ |x-3| &=4 &\;\;\;\;\;\;\;\;\;\;\;\;\;|x-3| &=4 \\ |-1-3| &\stackrel{?}{=} 4 &\;\;\;\;\;\;\;\;\;\;\;\;\; |7-3| &\stackrel{?}{=} 4 \\ |-4| &\stackrel{?}{=} 4 &\;\;\;\;\;\;\;\;\;\;\;\;\; |4| &\stackrel{?}{=} 4 \\ 4&=4 \;\; \checkmark &\;\;\;\;\;\;\;\;\;\;\;\;\; 4&=4 \;\; \checkmark \end{array}$

Absolute Value Inequalities

Now that you have the hang of solving absolute value equations describing a distance, let’s continue using the number line to solve absolute value inequalities. Place a circle whose radius is the given distance and center is a given value in the equation or inequality. The answer will leap out at you visually!

Example 4.4.3

Solve for $x$: $|x-3| < 4$

Solution

Compare this inequality to the equation in Example $4.4.2$.

Let’s begin the solution similarly: make a meaningful sentence of the inequality.

“The distance from the number $3$ to a number $x$ is less than $4$ units.”

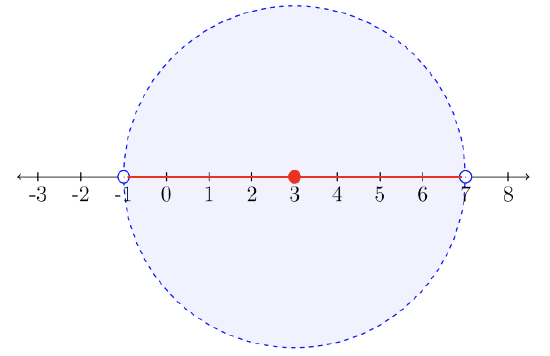
$clipboard_e161e2f11fed83382a13f4c0299c206e6.png$

The solution set will be all numbers within a distance of $4$ units from the number $3$. The circle marks the boundary of our inequality. The solution set is the numbers within the boundary. This time, the solution is an interval, describing all real numbers between $−1$ and $7$, not including $−1$ nor $7$.

Solution set: $\{x| − 1 < x < 7\}$ or the interval $(−1, 7)$.

Example 4.4.4

Solve for $t$: $|t-3| > 4$

Solution

Compare this inequality to the inequality in Example $4.4.3$.

Again, the meaningful application of distance is used to find the solution visually.

“The distance from the number $3$ to another number $t$ is greater than $4$ units.”

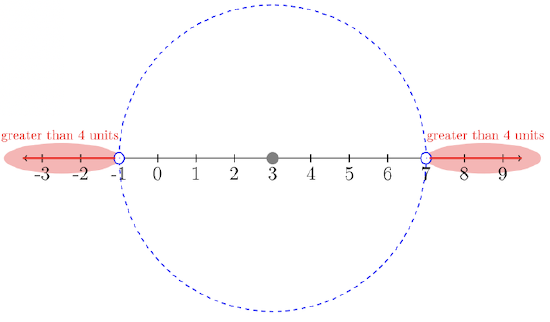
$clipboard_e01d5155bdb151958731963d1d69934e3.png$

The solution set will be all numbers beyond a distance of $4$ units from the number $3$. The circle marks the boundary of our inequality. The solution set is the numbers outside the circle’s boundary. The solution set is a compound inequality since the numbers excluded from the solution set are within the circle’s boundary.

Solution Set: $\{t| t < −1 \text{ or } t > 7\}$

Interval Notation: $(−∞, −1) ∪ (7, ∞)$

Example 4.4.5

Solve for $y$: $|y+2| \leq 5$

Solution

If we are to use distance to find a solution, our inequality must be converted to the absolute value of a difference.

We will use the following property of arithmetic to convert to a difference:

$A + B = A - (-B)$

Therefore:

$y+2 = y- (-2)$

We revise the stated inequality:

$|y − (−2)| ≤ 5$

In words,

“The distance from $-2$ to another number $y$ is less than or equal to $5$ units.”

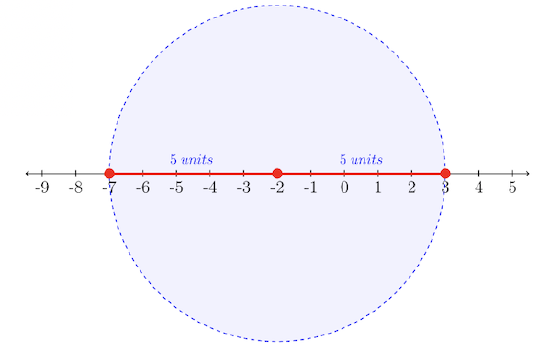
$clipboard_e6617c4077c6d367d3c5292c780e83d94.png$

The solution set will be all numbers within a distance of $5$ units from $−2$, including the values exactly $5$ units from $−2$. The visual solution leads us to our answer:

Solution Set: $\{y| − 7 ≤ y ≤ 3\}$

Interval Notation: $[−7, 3]$

Try It! (Exercises)

For each of the exercises #1-23,

Interpret the equation or inequality as distance, using a sentence.
Solve the inequality for the variable indicated, using distance.
Express the solution set in both set-builder notation and in interval notation.

$|x| = 6$
$|y| = 1$
$|b| = 3.26$
$|x| < 5$
$|y| > 4$
$|c| ≤ \dfrac{3}{4}$
$|q| ≥ 10.45$
$|p − 1| ≤ 2$
$|u − 2| > 3$
$|t − 4| ≤ 1$
$|x − 6.3| ≥ 4$
$|y − 3| < \dfrac{3}{2}$
$|h − 5| > \dfrac{3}{2}$
$\left|q − \dfrac{7}{2} \right| ≥ \dfrac{1}{2}$
$|w − 7| < 2.3$
$|r − 10| ≥ 0.15$
$|d − \pi| ≤ 2 \pi$
$|p − 2\pi| > \pi$
$\left|u − \dfrac{\pi}{2} \right| < \dfrac{\pi}{2}$
$|t + 4| ≤ 2$
$|x + 5| > 3$
$|r + 3| ≥ \dfrac{1}{4}$
$\left|a + \dfrac{1}{2} \right| <\dfrac{5}{2}$