5.4: Add and Subtract Rational Expressions

Last updated
Save as PDF

Page ID: 83140

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A fraction is a proportion. The fraction communicates the number of parts out of the whole.

$\dfrac{a}{b} \dfrac{\textcolor{blue}{\longleftarrow \text{The part is the numerator.}}}{\textcolor{blue}{\longleftarrow \text{The whole is the denominator.}}}$

For example, the egg carton pictured below contains $10$ eggs. Part of the eggs are brown ($7$ eggs) while the rest are white ($3$ eggs). A fraction $\dfrac{a}{b}$ quickly communicates the proportion of eggs that are brown or are white. Proportions can also be given as a decimal or percentage.

$clipboard_e3c5408e1d01cd0704f558548ac275e13.png$

Proportion of brown eggs: $\dfrac{7}{10} = 7 ÷ 10 = 0.7 = 70 \%$

Proportion of white eggs: $\dfrac{3}{10} = 3 ÷ 10 = 0.3 = 30 \%$

The proportion of brown and white eggs describes all of the eggs. Intuitively, we know this proportion is $100 \%$. The math should match our intuition, so let’s investigate.

$\begin{array} &70 \% + 30 \% &= 100 \% \\ \dfrac{7}{10} + \dfrac{3}{10} &= \dfrac{10}{10} \end{array}$

Our investigation leads us to deduce that we add the numerators, but not the denominators.

To Add or Subtract Fractions (Denominator is the Same)

Add or subtract the numerators.
Keep the same denominator.
Reduce if necessary.

\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\]

What works for real numbers also works for algebraic quantities. Algebra follows the same rules, which is an excellent anchor from which to perform your own algebraic investigations.

Example 5.4.1

Add $\dfrac{2x}{x+3} + \dfrac{x}{x+3}$

Solution

The denominators match. Add the two numerators, but keep the denominator.

$\dfrac{2x}{x+3} + \dfrac{x}{x+3} = \dfrac{2x+x}{x+3} = \dfrac{3x}{x+3}$

Since the result cannot be further simplified, the answer is $\dfrac{3x}{x+3}$

Example 5.4.2

Subtract $\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15}$

Solution

The denominators are the same. Subtract the numerators. Remember that each numerator is a quantity.

$\begin{array} &\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15} &= \dfrac{y^2+2y+8−(y^2+2)}{y^2−2y−15} &\text{Numerator: subtract the quantity \((y^2 + 2)$.} \\ & = \dfrac{y^2+2y+8−y^2−2}{y^2−2y−15} &\text{Each term of the quantity is subtracted.} \\ & = \dfrac{2y+6}{y^2−2y−15} &\text{The subtraction is complete.} \\& = \dfrac{2(y+3)}{(y−5)(y+3)} &\text{Factor numerator and denominator. Cancel.} \\ &= \dfrac{2}{y−5} &\text{The answer is most simplified.} \end{array}\)

Addition and Subtraction with Different Denominators

In order to add rational numbers or rational expressions, we need to find a common denominator. Create common denominators using equivalent fractions. That is, $\dfrac{a \cdot \textcolor{red}{d}}{b \cdot \textcolor{red}{d}} = \dfrac{ad}{bd}$. Then use the process for adding fractions with common denominators.

Example 5.4.3

Add $\dfrac{7}{75a^2b} + \dfrac{13}{180ab}$

Solution

To find the least common denominator, we play a game of “who has more?” for each denominator. Break down denominators into prime factors. Imagine that each denominator is a set of cards, and each card is a factor of the denominator. Because we have two denominators, we have two players who will play the game, “who has more?”. Whichever player has the most of a factor “wins,” and they place those cards into the winning pile. Ready to play?

Player #$1$: $75a^2 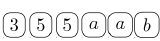\longrightarrow$ $clipboard_e82900e65b6134c70d503b2fed4be7096.png$

Player #$2$: $180ab 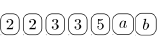\longrightarrow$ $clipboard_ec69093ffe99e21d390dcc4c691e250bf.png$

Who has more?	Player #$1$	Player #$2$	Winning Pile
$2$'s		$\checkmark$	$2 \cdot 2$
$3$'s		$\checkmark$	$3 \cdot 3$
$5$'s	$\checkmark$		$5 \cdot 5$
$a$'s	$\checkmark$		$a \cdot a$
$b$'s	TIE	TIE	$b$

The Winning Pile $= 2^2 \cdot 3^2 \cdot 5^2 \cdot a^2 \cdot b$

The Least Common Denominator $= 900a^2b$

Use the least common denominator to create a common denominator. Determine what factors are missing in each denominator. Multiply the missing factors to the denominator and also to the numerator. Then add.

$\dfrac{7}{75a^2b} + \dfrac{13}{180ab} = \dfrac{7 \textcolor{red}{\cdot 12}}{75a^2b \textcolor{red}{\cdot 12}} + \dfrac{13 \textcolor{red}{\cdot 5a}}{180ab \textcolor{red}{\cdot 5a}} = \dfrac{84}{900a^2b} + \dfrac{65a}{900a^2b} = \dfrac{84+65a}{900a^2b} $.

The answer is: $\dfrac{84+65a}{900a^2b}$

Example 5.4.4

Add $\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)}$

Solution

In the game of “who has more?” the quantities $(4y + 1)$ and $(y + 6)$ act as single numbers.

Player #$1$: $(4y + 1)^2 (y + 6) 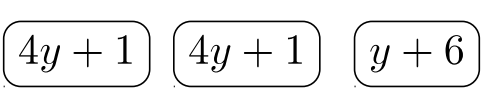\longrightarrow$ $clipboard_ee200f708cfb0a13a36f0a1987aee86af.png$

Player #$2$: $(4y + 1)(y + 6) 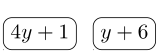\longrightarrow$ $clipboard_e96fc9cb8c18dcb8c3ca506179e29e468.png$

Winning Pile = $(4y + 1)^2 (y + 6)$ = Least Common Denominator

$\begin{array} &\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)} &= \dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5 \textcolor{red}{\cdot (4y+1)}}{(4y+1)(y+6) \textcolor{red}{\cdot (4y+1)}} \\ &= \dfrac{2y+1+(20y+5)}{(4y+1)^2(y+6)} &\text{Simplify the numerator, but leave the denominator in factored form.} \\ &= \dfrac{22y+6}{(4y+1)^2(y+6)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Tip: The numerator can be factored using GCF $= 2$: $22y + 6 = 2(11y + 3)$. However, this factorization does not lead to a cancellation. Therefore, the stated numerator is preferred.

Example 5.4.5

Subtract $\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6}$

Solution

To compare the factors of each denominator, we need to factor.

$ \begin{array} &&\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6} = \dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &\text{The denominators are factored.} \end{array}$

Play the game of “who has more?” to find the Least Common Denominator. Quantities act as single numbers.

Player #$1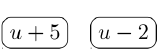$: $clipboard_e5b29d8142e8dc9709ca5f8f83c112282.png$

Player #$2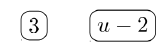$: $clipboard_e9db21ccf70da655263da0e7093153b56.png$

Winning Pile $= 3(u + 5)(u − 2) =$ Least Common Denominator

$\begin{array} &\dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &= \dfrac{\textcolor{red}{3}(u^2+2u)}{\textcolor{red}{3}(u+5)(u−2)} − \dfrac{2u \textcolor{red}{(u+5)}}{3(u−2) \textcolor{red}{(u+5)}} &\text{Determine the missing factors & multiply.} \\ &= \dfrac{3u^2+6u}{3(u+5)(u−2)} − \dfrac{2u^2+10u}{3(u+5)(u−2)} &\text{Simplify numerators.} \\ &= \dfrac{3u^2+6u−(2u^2+10u)}{3(u+5)(u−2)} &\text{Numerator: subtract the quantity.} \\ &= \dfrac{3u^2+6u−2u^2−10u}{3(u+5)(u−2)} &\text{Subtract each term of the quantity.} \\ &= \dfrac{u^2−4u}{3(u+5)(u−2)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Tip: The numerator can be factored using GCF $= u$: $u^2 − 4u = u(u − 4)$. However, this factorization does not lead to a cancellation. Therefore, the stated numerator is preferred.

Example 5.4.6

Subtract $\dfrac{3c}{49−c^2} − \dfrac{1}{c^2−7c}$

Solution

To compare the factors of each denominator, we need to factor.

$\begin{array} &&\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &\text{The denominators are factored.} \end{array}$

Play the game of “who has more?” to find the Least Common Denominator. Quantities act as single numbers.

Player #$1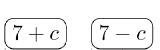$: $clipboard_e536c760e466e1d3499db5678220afecb.png$

Player #$2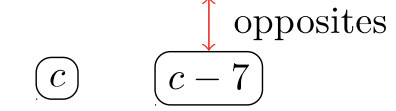$: $clipboard_e078fec96a07e13d83128820663fd76ea.png$

Note: $7 − c$ and $c − 7$ are opposites. Since they are opposites, one quantity can be made to “look like” the other.

$7 − c = −(c − 7)$

Next, bounce the negative to the numerator. Voilà! This is how we make a Least Common Denominator.

Winning Pile $= c(c + 7)(c − 7) =$ Least Common Denominator

$\begin{array} &\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &= \dfrac{3c}{\textcolor{red}{−}(c−7)(7+c)} −\dfrac{1}{c(c−7)} &\text{Replace \(7 − c$ with $−(c − 7)$.} \\& = \dfrac{\textcolor{red}{−}3c}{(c−7)(7+c)} − \dfrac{1}{c(c−7)} &\text{Since $\dfrac{a}{−b} = \dfrac{-a}{b}$, put the negative on top.} \\ & = \dfrac{−3c \cdot \textcolor{red}{c}}{\textcolor{red}{c}(c−7)(c+7)} − \dfrac{1 \textcolor{red}{\cdot (c+7)}}{c(c−7) \textcolor{red}{(c+7)}} &\text{Construct the LCD. Note: $7 + c = c + 7$.} \\ & = \dfrac{−3c^2−(c+7)}{c(c−7)(c+7)} &\text{Numerator: subtract the quantity.} \\ &= \dfrac{−3c^2−c−7}{c(c−7)(c+7)} &\text{The numerator has been simplified.} \\ &= \dfrac{− 3c^2+c+7}{c(c−7)(c+7)} &\text{Factor out $−1$.} \end{array}\)

Either of the last two lines could be your final answer. Which do you prefer? It’s your choice!

Note

After simplifying the numerator, pause and ask yourself, “what more can I do to simplify?” If the numerator is factorable, check to see if the factors are the same as those in the denominator. If so, cancel the common factors. Keep the denominator factored to remind yourself (and your reader) what factors do not cancel.

Try It! (Exercises)

For #1-20, add or subtract the rational expressions as indicated.

$\dfrac{5x}{3y^2} + \dfrac{x}{3y^2}$
$\dfrac{14a}{5b} − \dfrac{4a}{5b}$
$\dfrac{4r}{9qp} + \dfrac{1}{3q^2p}$
$\dfrac{1−n}{6n} + \dfrac{2n+1}{3n}$
$\dfrac{n+2}{12m^3} − \dfrac{2}{3m^3n}$
$\dfrac{t+6}{t+5} + \dfrac{t+4}{t+5}$
$\dfrac{6c+1}{(5c+2)^3} − \dfrac{c−1}{(5c+2)^3}$
$\dfrac{2}{x−3} + \dfrac{3}{10}$
$\dfrac{4}{y+2} + \dfrac{2}{3y+6}$
$\dfrac{3}{x+3} − \dfrac{3}{x−3}$
$\dfrac{h−2}{(h+1)^2} + \dfrac{2}{3h+3}$
$\dfrac{5}{y−1} − \dfrac{3}{y^2−1}$
$\dfrac{−2}{a^2−5a+6} + \dfrac{2}{a−3}$
$\dfrac{4}{d−3} − \dfrac{5d−12}{d^2−6d+9}$
$\dfrac{5}{v^2−5v} − \dfrac{v}{5v−25}$
$\dfrac{1−n}{n^2−4} − \dfrac{n−2}{n^2−2n−8}$
$3 + \dfrac{x}{ x+2}$
$\dfrac{3p−1}{p^2+5p+6} + \dfrac{2p−3}{p^2+3p+2}$
$\dfrac{3}{q+3} + \dfrac{2q}{q^2+8q+15}$
$\dfrac{w+2}{4w+16} − \dfrac{2}{w^2+4w}$

For #21-30, opposite quantities occur. Add or subtract the rational expressions as indicated.

$\dfrac{3}{8} + \dfrac{5}{−8}$
$\dfrac{y^2}{y−5} + \dfrac{4y+5}{5−y}$
$\dfrac{6}{w−2} + \dfrac{w+3}{2−w}$
$\dfrac{2a−7}{5a−8} + \dfrac{6+10a}{8−5a}$
$\dfrac{u^2−2}{2u^2−u−3} + \dfrac{u−2}{3−2u}$
$\dfrac{b−23}{b^2−b −20} − \dfrac{2}{5−b}$
$\dfrac{t+1}{t−1} − \dfrac{3t^2−1}{1−t^2}$
$\dfrac{2}{6−3x} + \dfrac{x}{x^2−4}$
$\dfrac{5r}{1−2r} − \dfrac{2r}{2r+1} + \dfrac{3}{4r^2−1}$
$\dfrac{2y}{y^2−9} − 1 + \dfrac{4}{3−y}$

Who has more?	Player #\(1\)	Player #\(2\)	Winning Pile
\(2\)'s		\(\checkmark\)	\(2 \cdot 2\)
\(3\)'s		\(\checkmark\)	\(3 \cdot 3\)
\(5\)'s	\(\checkmark\)		\(5 \cdot 5\)
\(a\)'s	\(\checkmark\)		\(a \cdot a\)
\(b\)'s	TIE	TIE	\(b\)