6.1: Simplify Radical Expressions

Last updated

Sep 15, 2021
Save as PDF
- 6: Radical Expressions
- 6.2: Add and Subtract Radical Expressions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Who doesn’t love the “undo” command on a computer? Radicals are like an undo command to all powers. If taking powers is a forward-action, then radicals require us to think backwards. To prepare for this section, memorize the first twelve perfect squares and the first five cubes. It will be very helpful to recognize powers of $2$ and $3$ .

Definition: Perfect Squares and Perfect Cubes to Memorize

Perfect Squares to memorize (first twelve):

$1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, …$

Cubes to memorize (first five):

$1, 8, 27, 64, 125, …$

Let’s look at the anatomy of a radical:

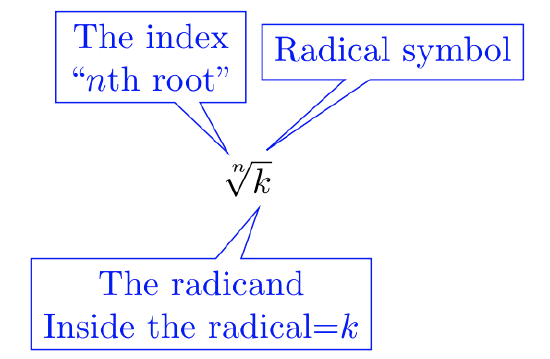
$clipboard_eaecd674719fbdb4cc9fbd5ec372189d8.png$

Index $n$	Example	Read Out Loud
Default Index $n=2$	$\sqrt{4}$	The square root of $4$ .
$n=3$	$\sqrt[3]{8}$	The cube root of $8$ .
$n=4$	$\sqrt[4]{16}$	The $4^{\text{th}}$ root of $16$ .
$n=5$	$\sqrt[5]{32}$	The $5^{\text{th}}$ root of $32$ .

The index, $n$ , indicates the exponent of the related power.

$\begin{array} &\sqrt{4} &= 2 &\text{Why? Because $2^2 = 4$.} \\ \sqrt[3]{8} &= 2 &\text{Why? Because $2^3 = 8$.} \\ \sqrt[4]{16} &= 2 &\text{Why? Because $2^4 = 16$.} \\ \sqrt[5]{32} &= 2 &\text{Why? Because $2^5 = 32$.} \end{array}$

All four examples above have a value of $2$ .

Example 6.1.1

Simplify.

$\sqrt{\dfrac{9}{64}}$
$\sqrt[3]{−64}$
$\sqrt{−81}$
$\sqrt[5]{100000}$

Solution

$\begin{array} & \sqrt{\dfrac{9}{64}} = \dfrac{3}{8} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{$\sqrt{\dfrac{9}{64}} = \dfrac{3}{8}$ because $\dfrac{3}{8} ≥ 0$ and $\left( \dfrac{3}{8} \right)^2 = \dfrac{9}{64}$.} \end{array}$
$\begin{array} & \sqrt[3]{−64} = −4 &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{$\sqrt[3]{−64} = −4$ because $n = 3$ is odd and $(−4)^3 = −64$.}\end{array}$
$\begin{array} & \sqrt{−81} \text{ is not a real number.} &\;\;\;\;\;\;\;\;\;\;\text{No real number, when squared, equals $−81$.}\end{array}$
$\begin{array} & \sqrt[5]{100000} = 10 &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{$\sqrt[5]{100000} = 10$ because $10^5 = 100000$.}\end{array}$

The properties and examples (below) will involve a radicand with variables. From here on out, we will assume that all variables of even-indexed radicals are nonnegative values. That is, for $\sqrt[n]{x^p}$ and $n$ is even, we will assume $x ≥ 0$ .

Property	Examples
1. $\sqrt[n]{a^n} = a$	$\sqrt[4]{x^4} = x$ or $\sqrt[3]{(-5)^3} = -5$
2. Product Property: $\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab}$	$\sqrt[5]{6} \cdot \sqrt[5]{x^2} = \sqrt[5]{6x^2}$ or $\sqrt{100x^4} = \sqrt{100} \cdot \sqrt{x^4} = 10x^2$
3. Quotient Property: $\sqrt[n]{\dfrac{a}{b}} = \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}$	$\sqrt{\dfrac{x^2}{100}} = \dfrac{\sqrt{x^2}}{\sqrt{100}} = \dfrac{x}{10}$ or $\dfrac{\sqrt[3]{54}}{\sqrt[3]{16}} = \sqrt[3]{\dfrac{54}{16}} = \sqrt[3]{\dfrac{27}{8}} = \dfrac{3}{2}$

Definition

Let $m$ and $n$ be integers such that $m/n$ is a rational number in lowest terms and $n > 1$ . Then,

$a^{1/n} = \sqrt[n]{a}$ and $a^{m/n} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m$

If $n$ is even, then we require $a ≥ 0$ .

Example 6.1.2

Write each expression in radical notation, then simplify.

$(81x^2)^{−1/2}$
$(243)^{3/5}$

Solution

$(81x^2)^{−1/2} = \dfrac{1}{\sqrt{81x^2}} = \dfrac{1}{9x}$
$(243)^{3/5} = \sqrt[5]{243^3} = \sqrt[5]{(3^5)^3} = \sqrt[5]{(3^3)^5} = 3^3 = 27$

Simplifying Radicals

Use as often as possible the property $\sqrt[n]{a^n} = a$ to simplify radicals. Factor into chunks where powers equal the index $n$ , then set those numbers or variable free from the radical! Again, you may assume in all problems that variables represent positive real numbers.

Example 6.1.3

$\sqrt{12x^5y^3}$
$5\sqrt[3]{216u^6v^5}$
$−\sqrt[4]{16a^{23}}$

Solution

$\begin{array} &\sqrt{12x^5y^3} &= \sqrt{12} \cdot \sqrt{x^5} \cdot \sqrt{y^3} &\text{The product property: simplify $3$ separate radicals.} \\ &= \sqrt{\textcolor{red}{2^2} \cdot 3} \cdot \sqrt{\textcolor{red}{x^2} \cdot \textcolor{red}{x^2} \cdot x} \cdot \sqrt{\textcolor{red}{y^2} \cdot y} &\text{The index $n = 2$. Find powers of $2$ to simplify.} \\ &= \sqrt{2^2 \cdot x^2 \cdot x^2 \cdot y^2} \cdot \sqrt{3xy} &\text{Group the squares. Group the non-squares.} \\ &= 2 \cdot x \cdot x \cdot y \cdot \sqrt{3xy}n &\text{Simplify using $\sqrt[n]{a^n} = a$.} \\ &= 2x^2y \sqrt{3xy} &\text{Combine powers to simplify.} \end{array}$

$\begin{array} &5\sqrt[3]{216u^6v^5} &= 5\sqrt[3]{216} \cdot \sqrt[3]{u^6} \cdot \sqrt[3]{v^5} &\;\;\;\text{The product property: simplify $3$ separate radicals.} \\ &= 5 \cdot \sqrt[3]{\textcolor{red}{6^3}} \cdot \sqrt[3]{\textcolor{red}{(u^2)^3}} \cdot \sqrt[3]{\textcolor{red}{v^3} \cdot v^2} &\;\;\;\text{The index $n = 3$. Find powers of $3$ to simplify.} \\ &= 5 \cdot \sqrt[3]{6^3 \cdot (u^2)^3 \cdot v^3} \cdot \sqrt[3]{v^2} &\;\;\;\text{Group the cubes. Group the non-cubes.} \\ &= 5 \cdot 6 \cdot u^2 \cdot v \cdot \sqrt[3]{v^2} &\;\;\;\text{Simplify using $\sqrt[n]{a^n} = a$.} \\ &= 30u^2v\sqrt[3]{v^2} &\;\;\;\text{Combine powers to simplify.} \end{array}$

$\begin{array} &−\sqrt[4]{16a^{23}} &= -1 \cdot \sqrt[4]{16} \cdot \sqrt[4]{a^{23}} &\;\;\;\;\;\;\;\;\;\;\;\text{The product property: simplify $2$ separate radicals.} \\ &= −1 \cdot \sqrt[4]{\textcolor{red}{2^4}} \cdot \sqrt[4]{\textcolor{red}{(a^5)^4} \cdot a^3} &\;\;\;\;\;\;\;\;\;\;\;\text{How many times does $4$ go into $23$ evenly? $5$. $R=3$.} \\ &= −1 \cdot \sqrt[4]{4^2 \cdot (a^5)^4} \cdot \sqrt[4]{a^3} &\;\;\;\;\;\;\;\;\;\;\;\text{Group powers of $4$. Group non-powers of $4$.} \\ &= −1 \cdot 2 \cdot a^5 \cdot \sqrt[4]{a^3} &\;\;\;\;\;\;\;\;\;\;\;\text{Simplify using $\sqrt[n]{a^n} = a$.} \\ &= -2a^5 \sqrt[4]{a^3} &\;\;\;\;\;\;\;\;\;\;\;\text{Combine powers to simplify.} \end{array}$

Example 6.1.4

Multiply and simplify $\sqrt[3]{4p^2q^3} \cdot \sqrt[3]{6pq}$

Solution

$\begin{array} &\sqrt[3]{4p^2q^3} \cdot \sqrt[3]{6pq} &= \sqrt[3]{4 \cdot 6 \cdot p^2 \cdot p \cdot q \cdot q} &\text{The product property consolidates the radical.} \\ &= \sqrt[3]{24 \cdot p^3 \cdot q^2} &\text{Consolidate the powers using power properties.} \\ &= \sqrt[3]{\textcolor{red}{2^3} \cdot 3} \cdot \sqrt[3]{\textcolor{red}{p^3}} \cdot \sqrt[3]{q^2} &\text{The product property: simplify $3$ separate radicals.} \\ &= −\sqrt[3]{2^3 \cdot p^3} \cdot \sqrt[3]{3q^2} &\text{Group the cubes. Group the non-cubes.} \\ &= 2p \cdot \sqrt[3]{3q^2} &\text{Simplify using $\sqrt[n]{a^n} = a$.} \end{array}$

Try It! (Exercises)

1. In Example $6.1.2$ b of this section, it is stated: $\sqrt[5]{(3^5)^3} = \sqrt[5]{(3^3)^5}$ .

Name the properties which allows us to equate $(3^5)^3 = (3^3)^5$ . Explain.

2. Use the equivalency $x^{ab} = x^{ba}$ to simplify each of the following without using a calculator.

$\sqrt[3]{(7^3)^{10}}$
$\sqrt[4]{(5^4)^3}$
$8\sqrt[5]{(-10^5)^4}$

3. For each of the following, replace the stated number as a power of the index. Use the equivalency $x^{ab} = x^{ba}$ to simplify each of the following.

For example: $\sqrt[3]{8^5} = \sqrt[3]{(2^3)^5} = \sqrt[3]{(2^5)^3} = 2^5 = 32$ .

$\sqrt{16^5}$
$−5\sqrt[4]{81^7}$
$−9\sqrt[5]{32^6}$

For 4-11, write each expression in radical notation, then simplify without a calculator.

$121^{−1/2}$
$32^{2/5}$
$125^{−2/3}$
$(−125)^{2/3}$
$\left( \dfrac{81}{100} \right)^{1/2}$
$\left( \dfrac{64}{125} \right)^{2/3}$
$\left(−\dfrac{64}{125} \right)^{2/3}$
$\left( \dfrac{64}{125} \right)^{−2/3}$

For 12-23, simplify the expression. Assume that variables represent positive real numbers.

$\sqrt{18y^3}$
$\sqrt[3]{250b^5}$
$\sqrt[4]{48x^9}$
$\sqrt[5]{−243c^{10}}$
$−2a \sqrt[10]{80a}$
$\dfrac{\sqrt[3]{500u^5}}{45u}$
$\sqrt[4]{\dfrac{1250p^9}{p^{13}}}$
$\dfrac{3}{4} \sqrt{\dfrac{96z^{20}}{6}}$
$\sqrt{128n^{10}m^3}$
$\sqrt[4]{\dfrac{405x^{14}y^6}{5x^4y}}$
$(\sqrt[7]{a^5b^6})^{35}$
$\left( \dfrac{\sqrt[3]{8u^6v^{12}}}{6u^2v} \right)^2$

For 24-31, multiply and simplify. Assume that variables represent positive real numbers.

$−3x \sqrt{5x} \cdot \sqrt{20x^3}$
$2q \sqrt[3]{54q^2} \cdot \sqrt[3]{4q^4}$
$6t^3 (\sqrt[4]{75t^6} \cdot \sqrt[4]{100t^3})$
$\sqrt[5]{64u^5v^8 } \cdot \sqrt[5]{112v^4} \cdot 7v$
$\dfrac{\sqrt{5x}}{10} \cdot \dfrac{\sqrt{15x}}{3x}$
$\dfrac{1}{2} \left( \dfrac{\sqrt[3]{18a^2}}{2} \right) \left( \dfrac{\sqrt[3]{6a^4}}{3a} \right)$
$\sqrt[3]{\dfrac{56n^4}{27m^5}} \cdot \sqrt[3]{\dfrac{49m^2}{8n}}$
$\left( \dfrac{24w^{11}}{13} \right)^3 \left( \dfrac{13w}{6} \right)^3$

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Perfect Squares and Perfect Cubes to Memorize

Example 6.1.1

Definition

Example 6.1.2

Example 6.1.3

Example 6.1.4

Simplifying Radicals

Try It! (Exercises)

Support Center

How can we help?