6.2: Add and Subtract Radical Expressions

Rules for radical multiplication and division have a simplicity and ease which lulls students into thinking addition and subtraction will follow suit. However, rules for addition and subtraction have more complication and less flexibility. Let’s start with the most common pitfall:

$\sqrt[n]{a} + \sqrt[n]{b} \neq \sqrt[n]{a+b}$

Note: The symbol $\neq$ says “does not equal.”

These two examples have even more temptation to go wrong due to the squaring and the variables:

$\sqrt{x^2 + y^2} \neq x+y$

Also,

$\sqrt{x^2 - y^2} \neq x-y$

This doesn’t change any property that was previously introduced! The following still holds true! ( $x ≥ 0$ and $y ≥ 0$ if $n$ is even)

$\sqrt{x^2} + \sqrt{y^2} = x + y$

And

$\sqrt{x^2} - \sqrt{y^2} = x - y$

And in general,

$\sqrt[n]{x^n} + \sqrt[n]{y^n} = x ± y$

Use a calculator to convince yourself:

$\sqrt{6} + \sqrt{2} \neq \sqrt{8}$

On the left side, find the value $\sqrt{6} + \sqrt{2}$ to the nearest hundredth:

$\sqrt{6} + \sqrt{2} ≈ 3.86$

On the right side,

$\sqrt{8} ≈ 2.83$

Now we see radicands cannot be added:

$3.86 \neq 2.83$

Use the order of operations as the problem is presented. Any other order of computation could be a pitfall.

$\textcolor{green}{\checkmark} \sqrt[3]{27} + \sqrt[3]{8} = 3+ 2 =5$

The order of operations tells us to take the cube root first, then add. Use the order shown and it will be correct!

Using “Like Terms” to Add or Subtract “Like Radicands”

Adding and subtracting radicals starts with simplifying radicals. Use as often as possible the property $\sqrt[n]{a^n} = a$ to simplify radicals. We will continue to assume the variables take on nonnegative values only. Let’s explore how gathering like terms can be used with radicals.

$2x + x = 3x$ $x =$ any real number

Gathering like terms is a technique you’ve used countless times before. Why not use with radicals? Radicals are real numbers, too! This approach opens our toolbox for adding or subtracting radical expressions. We can add radicals if the radicand is identical and index $n$ also matches.

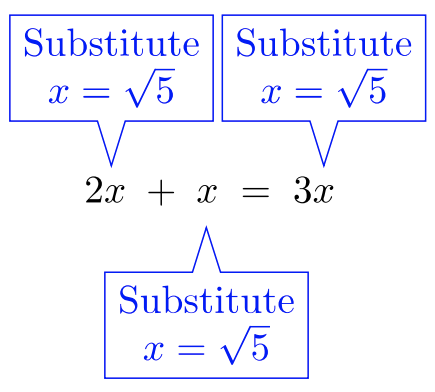
Suppose $x = \sqrt{5}$. Gather like radicals:

$2\sqrt{5} + \sqrt{5} = 3\sqrt{5}$

Definition: Like Radicals

Two radical terms are said to be like radicals if they have the same index and the same radicand.

Example 6.2.1

Which of the three expressions can be simplified? Explain.

1. $4 \sqrt[3]{10} + 7 \sqrt[3]{10}$
2. $3 \sqrt{2} + 3 \sqrt{11}$
3. $\sqrt[3]{6} + \sqrt{6}$

Solution

1. This is the only given expression of the three that can be simplified.

$4 \sqrt[3]{10} + 7 \sqrt[3]{10} = 11\sqrt[3]{10}$

$4 \sqrt[3]{10} \text{ and } 7 \sqrt[3]{10}$ both contain $\sqrt[3]{10}$ as the like radicals.

2. Cannot be simplified.

$3 \sqrt{2} \neq 3 \sqrt{11}$

The radicands are not equal.

3. Cannot be simplified.

$\sqrt[3]{6} \neq \sqrt{6}$

The indices are not equal.

Simplify First

Don’t see a match? Make sure your radicals are completely simplified before you attempt to add or subtract radicals. The following examples demonstrate how simplification can help you find like radicals.

Example 6.2.2

Simplify $\sqrt{75} + 2 \sqrt{12} − \sqrt{3}$

Solution

$\begin{array} &\sqrt{75} + 2 \sqrt{12} − 5 \sqrt{3}& &\text{At first glance, none of the radicals are like radicals. However, both \(\sqrt{75}\) and \(\sqrt{12}\) can be simplified.} \\ & = \sqrt{25 \cdot 3} + 2 \sqrt{4 \cdot 3} − \sqrt{3} &\text{Factor perfect squares within each radicand.} \\ &= 5\sqrt{3} + 2 \cdot 2 \sqrt{3} − \sqrt{3} &\text{Simplify.} \\ &= 5\sqrt{3} + 4\sqrt{3} − \sqrt{3} &\text{Combine like radicals.} \\ (5 + 4 − 1)\sqrt{3} &= 8\sqrt{3} & \end{array}$

Example 6.2.3

Add $\sqrt[3]{54x^2} + \sqrt[3]{3x^2} + \sqrt[3]{16x^2}$

Solution

$\begin{array} &&\sqrt[3]{54x^2} + \sqrt[3]{3x^2} + \sqrt[3]{16x^2} &\text{Simplify each radical.} \\ &= \sqrt[3]{27 \cdot 2x^2} + \sqrt[3]{3x^2} + \sqrt[3]{8 \cdot 2x^2} &\text{Factor the radicands.} \\ &= 3 \textcolor{red}{\sqrt[3]{2x^2}} + \sqrt[3]{3x^2} + 2 \textcolor{red}{\sqrt[3]{3x^2}} &\text{Two terms contain like radicals. Simplify. } \\ &= 5 \sqrt[3]{3x^2} + \sqrt[3]{3x^2} & \end{array}$

Example 6.2.4

Find the area and the perimeter of the rectangle shown.

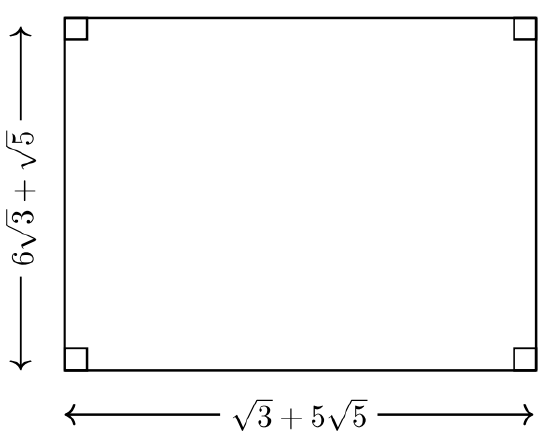
Length $= (6 \sqrt{3} + \sqrt{5})$ feet

Width $= (\sqrt{3} + 5\sqrt{5})$ feet

Solution

Use FOIL:

$\begin{array} &&\text{Area } &= (6 \sqrt{3} + \sqrt{5})(\sqrt{3} + 5\sqrt{5}) &= \underbrace{(6 \sqrt{3})(\sqrt{3})}_{\text{F}} + \underbrace{(6 \sqrt{3})(5\sqrt{5})}_{\text{O}} + \underbrace{(\sqrt{5})(\sqrt{3})}_{\text{I}} + \underbrace{(\sqrt{5})(5\sqrt{5})}_{\text{L}} \\ &&&= 6 \cdot 3 + 6 \cdot 5 \cdot \sqrt{3 \cdot 5} + \sqrt{5 \cdot 3} + 5 \cdot 5 \\&&&= 18 + 30\sqrt{15} + \sqrt{15} +25 \\&&&= 43 +31\sqrt{15} \text{ ft}^2 \end{array}$

$\begin{array} &&\text{Perimeter } &= \overbrace{2(6 \sqrt{3} + \sqrt{5}) + 2(\sqrt{3} + 5\sqrt{5})}^{P = 2L + 2W} &= \underbrace{(2 \cdot 6 \sqrt{3} + 2 \cdot \sqrt{5})}_{\text{Distributive Property}} + \underbrace{(2 \cdot \sqrt{3} + 2 \cdot 5\sqrt{5})}_{\text{Distributive Property}} \\ &&&= (12 \sqrt{3} + 2 \sqrt{5}) + (2 \sqrt{3} + 2 \cdot 5\sqrt{5}) \\&&&= \underbrace{12 \sqrt{3} + 2\sqrt{3}}_{\text{Like Radicals}} + \underbrace{2\sqrt{5}+10\sqrt{5}}_{\text{Like Radicals}} \\&&&= 14\sqrt{3} + 12\sqrt{5} \text{ ft}^2 \end{array}$

Try It! (Exercises)

For #1-4, add or subtract the expressions, if possible. Assume the variables represent nonnegative numbers.

1. $7\sqrt{5} − 2\sqrt{5} + \sqrt{5}$
2. $3\sqrt{3x} − 4\sqrt{3x} + 6\sqrt{6x} − 8\sqrt{6x}$
3. $\sqrt[3]{9y} + \sqrt[4]{9y} − \sqrt[3]{2y} + 2\sqrt[4]{9y}$
4. $7b \sqrt[5]{16b^2} − 4b\sqrt[3]{16b^2} − 3b\sqrt[5]{3b^2}$

For #5-8, simplify each radical expression, then add or subtract the expressions, if possible. Assume the variables represent nonnegative numbers.

5. $2\sqrt{3a^3} + 5a\sqrt{3a} − \sqrt{27a^3}$
6. $\sqrt[3]{56c^6} − 2c^2 \cdot \sqrt[3]{189} + \sqrt[3]{7c^2}$
7. $3\sqrt[4]{4p^7} − 3p\sqrt[4]{324p^3} + 2\sqrt[4]{64p^7}$
8. $2b\sqrt[5]{192b^3} − \sqrt[5]{64b} + 3\sqrt[5]{6b^8} + \sqrt[5]{486b}$

For #9-14, evaluate each of the following. Simplify wherever possible. Assume the variables represent nonnegative numbers.

9. $\sqrt{12}(\sqrt{2} − \sqrt{18})$
10. $(7\sqrt[3]{10} + 3\sqrt[3]{4})(2\sqrt[3]{20} − \sqrt[3]{50})$
11. $(9\sqrt{2x} + 6\sqrt{3x})^2$
12. $(\sqrt{26} − 4\sqrt{10})(\sqrt{26} + 4\sqrt{10})$
13. $(\sqrt[3]{24} − \sqrt[3]{54})^2$
14. $5(3\sqrt{7} − 1)(4\sqrt{14} + 1)$

For #15-16, find the area and the perimeter of each rectangle. The length and width are each marked in the figures and the units are feet.

15. 
16. 
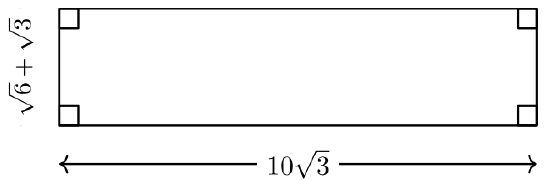
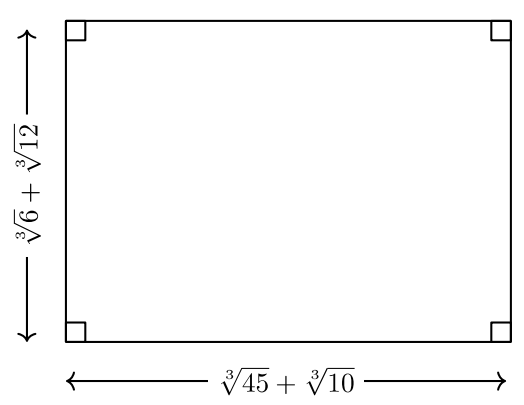
17. A square has side lengths = $(\sqrt[4]{4} + 2)$ feet. Find each of the area and the perimeter of the square.
18. If a square has area $= 540$ $\text{ft}^2$. What is the perimeter of the square?