2.1: Linear Functions
- Page ID
- 80764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We now begin the study of families of functions. Our first family, linear functions, are old friends as we shall soon see. Recall from Geometry that two distinct points in the plane determine a unique line containing those points, as indicated below.
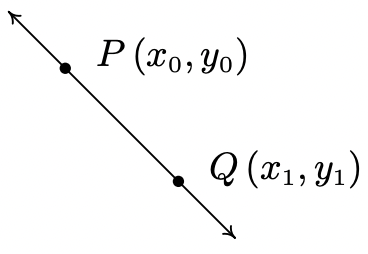
To give a sense of the ‘steepness’ of the line, we recall that we can compute the slope of the line using the formula below.
The slope \(\ m\) of the line containing the points \(\ P\left(x_{0}, y_{0}\right)\) and \(\ Q\left(x_{1}, y_{1}\right)\) is:
\(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}},\)
provided \(\ x_{1} \neq x_{0}\).
A couple of notes about Equation 2.1 are in order. First, don’t ask why we use the letter \(\ ‘m’\) to represent slope. There are many explanations out there, but apparently no one really knows for sure.1 Secondly, the stipulation \(\ x_{1} \neq x_{0}\) ensures that we aren’t trying to divide by zero. The reader is invited to pause to think about what is happening geometrically; the anxious reader can skip along to the next example.
Find the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
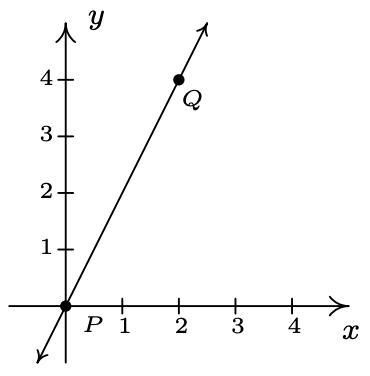
- \(\ P(0,0), Q(2,4)\)
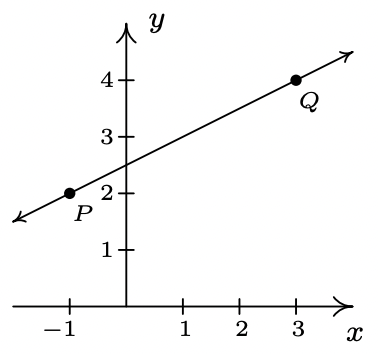
- \(\ P(-1,2), Q(3,4)\)
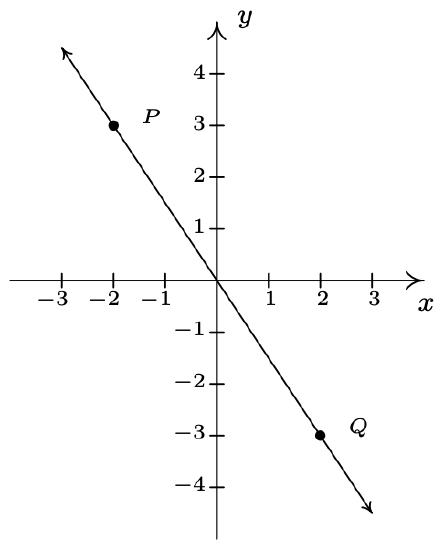
- \(\ P(-2,3), Q(2,-3)\)
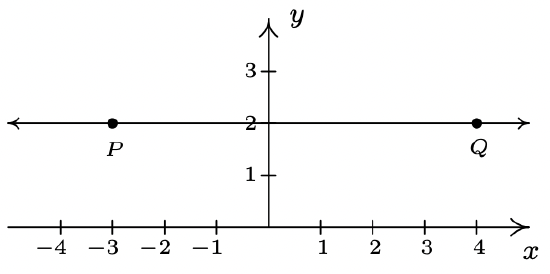
- \(\ P(-3,2), Q(4,2)\)
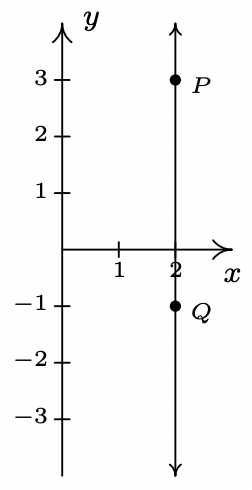
- \(\ P(2,3), Q(2,-1)\)
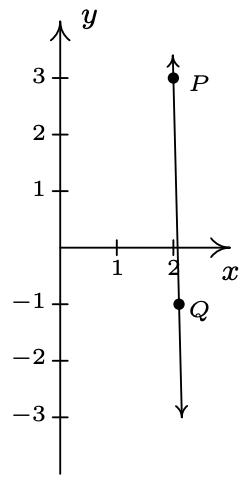
- \(\ P(2,3), Q(2.1,-1)\)
Solution
In each of these examples, we apply the slope formula, Equation 2.1.
- \(\ m=\frac{4-0}{2-0}=\frac{4}{2}=2\)
- \(\ m=\frac{4-2}{3-(-1)}=\frac{2}{4}=\frac{1}{2}\)
- \(\ m=\frac{-3-3}{2-(-2)}=\frac{-6}{4}=-\frac{3}{2}\)
- \(\ m=\frac{2-2}{4-(-3)}=\frac{0}{7}=0\)
- \(\ m=\frac{-1-3}{2-2}=\frac{-4}{0}\), which is undefined
- \(\ m=\frac{-1-3}{2.1-2}=\frac{-4}{0.1}=-40\)
A few comments about Example 2.1.1 are in order. First, for reasons which will be made clear soon, if the slope is positive then the resulting line is said to be increasing. If it is negative, we say the line is decreasing. A slope of 0 results in a horizontal line which we say is constant, and an undefined slope results in a vertical line.2 Second, the larger the slope is in absolute value, the steeper the line. You may recall from Intermediate Algebra that slope can be described as the ratio \(\ \frac{\text { ‘rise’ }}{\text { run }}\). For example, in the second part of Example 2.1.1, we found the slope to be 1 2 . We can interpret this as a rise of 1 unit upward for every 2 units to the right we travel along the line, as shown below.
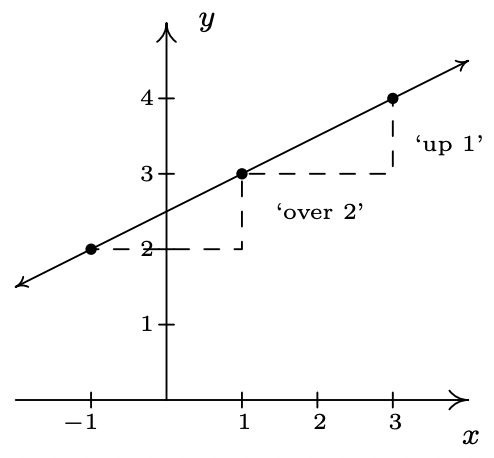
Using more formal notation, given points \(\ \left(x_{0}, y_{0}\right)\) and \(\ \left(x_{1}, y_{1}\right)\), we use the Greek letter delta \(\ \text{‘}\Delta\text{’}\) to write \(\ \Delta y=y_{1}-y_{0}\) and \(\ \Delta x=x_{1}-x_{0}\). In most scientific circles, the symbol \(\ \Delta\) means ‘change in’. Hence, we may write
\(\ m=\frac{\Delta y}{\Delta x},\)
which describes the slope as the rate of change of \(\ y\) with respect to \(\ x\). Rates of change abound in the ‘real world’, as the next example illustrates.
Suppose that two separate temperature readings were taken at the ranger station on the top of Mt. Sasquatch: at 6 AM the temperature was \(\ 24^{\circ} \mathrm{F}\) and at 10 AM it was \(\ 32^{\circ} \mathrm{F}\).
- Find the slope of the line containing the points (6, 24) and (10, 32).
- Interpret your answer to the first part in terms of temperature and time.
- Predict the temperature at noon.
Solution
- For the slope, we have \(\ m=\frac{32-24}{10-6}=\frac{8}{4}=2\).
- Since the values in the numerator correspond to the temperatures in \(\ { }^{\circ} \mathrm{F}\), and the values in the denominator correspond to time in hours, we can interpret the slope as \(\ 2=\frac{2}{1}=\frac{2^{\circ} \mathrm{F}}{1 \text { hour }}\), or \(\ 2^{\circ} \mathrm{F}\) per hour. Since the slope is positive, we know this corresponds to an increasing line. Hence, the temperature is increasing at a rate of \(\ 2^{\circ} \mathrm{F}\) per hour.
- Noon is two hours after 10 AM. Assuming a temperature increase of \(\ 2^{\circ} \mathrm{F}\) per hour, in two hours the temperature should rise \(\ 4^{\circ} \mathrm{F}\). Since the temperature at 10 AM is \(\ 32^{\circ} \mathrm{F}\), we would expect the temperature at noon to be \(\ 32+4=36^{\circ} \mathrm{F}\).
Now it may well happen that in the previous scenario, at noon the temperature is only \(\ 33^{\circ} \mathrm{F}\). This doesn’t mean our calculations are incorrect, rather, it means that the temperature change throughout the day isn’t a constant \(\ 2^{\circ} \mathrm{F}\) per hour. As discussed in Section 1.4.1, mathematical models are just that: models. The predictions we get out of the models may be mathematically accurate, but may not resemble what happens in the real world.
In Section 1.2, we discussed the equations of vertical and horizontal lines. Using the concept of slope, we can develop equations for the other varieties of lines. Suppose a line has a slope of m and contains the point \(\ \left(x_{0}, y_{0}\right)\). Suppose \(\ (x, y)\) is another point on the line, as indicated below.
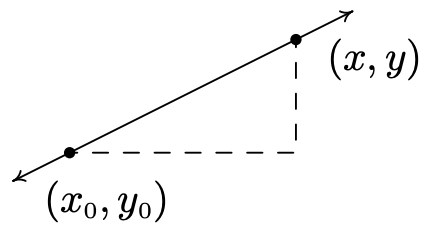
Equation 2.1 yields
\(\ \begin{aligned}
m &=\frac{y-y_{0}}{x-x_{0}} \\
m\left(x-x_{0}\right) &=y-y_{0} \\
y-y_{0} &=m\left(x-x_{0}\right)
\end{aligned}\)
We have just derived the point-slope form of a line.3
The point-slope form of the line with slope \(\ m\) containing the point \(\ \left(x_{0}, y_{0}\right)\) is the equation \(\ y-y_{0}=m\left(x-x_{0}\right)\).
Write the equation of the line containing the points (−1, 3) and (2, 1).
Solution
In order to use Equation 2.2 we need to find the slope of the line in question so we use Equation 2.1 to get \(\ m=\frac{\Delta y}{\Delta x}=\frac{1-3}{2-(-1)}=-\frac{2}{3}\). We are spoiled for choice for a point \(\ \left(x_{0}, y_{0}\right)\). We’ll use (−1, 3) and leave it to the reader to check that using (2, 1) results in the same equation. Substituting into the point-slope form of the line, we get
\(\ \begin{aligned}
y-y_{0} &=m\left(x-x_{0}\right) \\
y-3 &=-\frac{2}{3}(x-(-1)) \\
y-3 &=-\frac{2}{3}(x+1) \\
y-3 &=-\frac{2}{3} x-\frac{2}{3} \\
y &=-\frac{2}{3} x+\frac{7}{3}.
\end{aligned}\)
We can check our answer by showing that both (−1, 3) and (2, 1) are on the graph of \(\ y=-\frac{2}{3} x+\frac{7}{3}\) algebraically, as we did in Section 1.2.1.
In simplifying the equation of the line in the previous example, we produced another form of a line, the slope-intercept form. This is the familiar \(\ y = mx + b\) form you have probably seen in Intermediate Algebra. The ‘intercept’ in ‘slope-intercept’ comes from the fact that if we set \(\ x = 0\), we get \(\ y = b\). In other words, the y-intercept of the line \(\ y = mx + b\) is \(\ (0, b)\).
The slope-intercept form of the line with slope \(\ m\) and y-intercept \(\ (0, b)\) is the equation \(\ y = mx + b\).
Note that if we have slope \(\ m = 0\), we get the equation \(\ y = b\) which matches our formula for a horizontal line given in Section 1.2. The formula given in Equation 2.3 can be used to describe all lines except vertical lines. All lines except vertical lines are functions (Why is this?) so we have finally reached a good point to introduce linear functions.
A linear function is a function of the form
\(\ f(x)=m x+b,\)
where \(\ m\) and b are real numbers with \(\ m \neq 0\). The domain of a linear function is \(\ (-\infty, \infty)\).
For the case \(\ m = 0\), we get \(\ f(x) = b\). These are given their own classification.
A constant function is a function of the form
\(\ f(x)=b,\)
where \(\ b\) is real number. The domain of a constant function is \(\ (-\infty, \infty)\).
Recall that to graph a function, \(\ f\), we graph the equation \(\ y = f(x)\). Hence, the graph of a linear function is a line with slope \(\ m\) and y-intercept \(\ (0, b)\); the graph of a constant function is a horizontal line (a line with slope \(\ m = 0\)) and a y-intercept of \(\ (0, b)\). Now think back to Section 1.6.1, specifically Definition 1.10 concerning increasing, decreasing and constant functions. A line with positive slope was called an increasing line because a linear function with \(\ m > 0\) is an increasing function. Similarly, a line with a negative slope was called a decreasing line because a linear function with \(\ m < 0\) is a decreasing function. And horizontal lines were called constant because, well, we hope you’ve already made the connection.
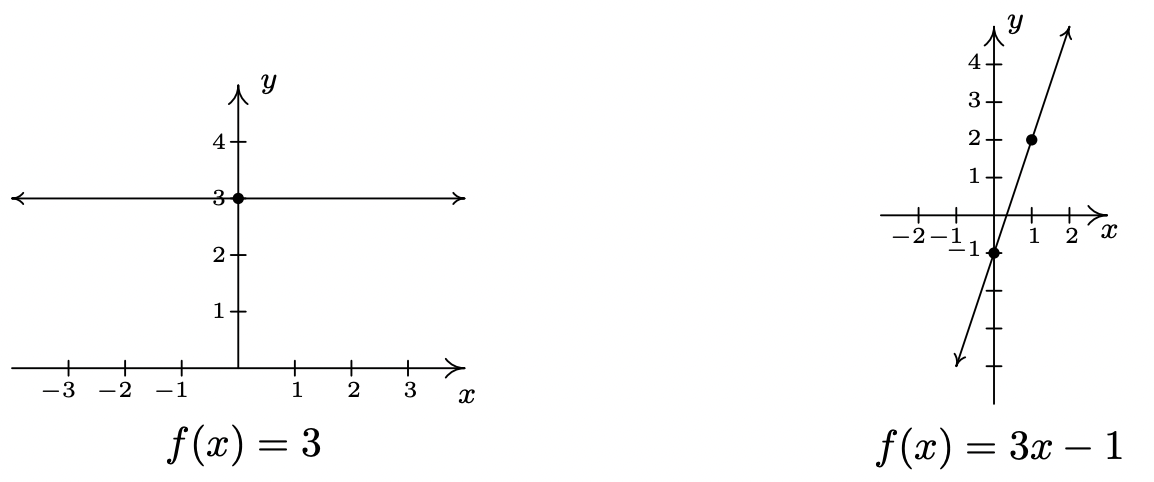
Graph the following functions. Identify the slope and y-intercept.
- \(\ f(x) = 3\)
- \(\ f(x) = 3x − 1\)
- \(\ f(x)=\frac{3-2 x}{4}\)
- \(\ f(x)=\frac{x^{2}-4}{x-2}\)
Solution
- To graph \(\ f(x) = 3\), we graph \(\ y = 3\). This is a horizontal line (\(\ m = 0\)) through (0, 3).
- The graph of \(\ f(x) = 3x − 1\) is the graph of the line \(\ y = 3x − 1\). Comparison of this equation with Equation 2.3 yields \(\ m = 3\) and \(\ b = −1\). Hence, our slope is 3 and our y-intercept is (0, −1). To get another point on the line, we can plot \(\ (1, f(1)) = (1, 2)\).
- At first glance, the function \(\ f(x)=\frac{3-2 x}{4}\) does not fit the form in Definition 2.1 but after some rearranging we get \(\ f(x)=\frac{3-2 x}{4}=\frac{3}{4}-\frac{2 x}{4}=-\frac{1}{2} x+\frac{3}{4}\). We identify \(\ m=-\frac{1}{2}\) and \(\ b=\frac{3}{4}\). Hence, our graph is a line with a slope of \(\ -\frac{1}{2}\) and a y-intercept of \(\ \left(0, \frac{3}{4}\right)\). Plotting an additional point, we can choose \(\ (1, f(1))\) to get \(\ \left(1, \frac{1}{4}\right)\).
- If we simplify the expression for \(\ f\), we get
\(\ f(x)=\frac{x^{2}-4}{x-2}=\frac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}}=x+2\).
If we were to state \(\ f(x) = x + 2\), we would be committing a sin of omission. Remember, to find the domain of a function, we do so before we simplify! In this case, \(\ f\) has big problems when \(\ x = 2\), and as such, the domain of \(\ f\) is \(\ (-\infty, 2) \cup(2, \infty)\). To indicate this, we write \(\ f(x) = x + 2\), \(\ x \neq 2\). So, except at \(\ x = 2\), we graph the line \(\ y = x + 2\). The slope \(\ m = 1\) and the y-intercept is (0, 2). A second point on the graph is \(\ (1, f(1)) = (1, 3)\). Since our function f is not defined at \(\ x = 2\), we put an open circle at the point that would be on the line \(\ y = x + 2\) when \(\ x = 2\), namely (2, 4).
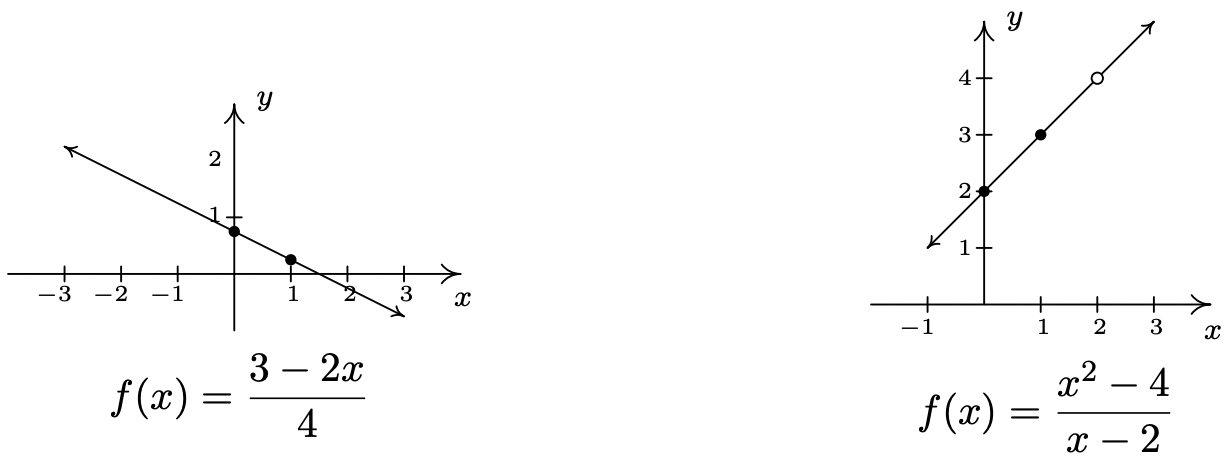
The last two functions in the previous example showcase some of the difficulty in defining a linear function using the phrase ‘of the form’ as in Definition 2.1, since some algebraic manipulations may be needed to rewrite a given function to match ‘the form’. Keep in mind that the domains of linear and constant functions are all real numbers \(\ (-\infty, \infty)\), so while \(\ f(x)=\frac{x^{2}-4}{x-2}\) simplified to a formula \(\ f(x) = x + 2\), \(\ f\) is not considered a linear function since its domain excludes \(\ x = 2\). However, we would consider
\(\ f(x)=\frac{2 x^{2}+2}{x^{2}+1}\)
to be a constant function since its domain is all real numbers (Can you tell us why?) and
\(\ f(x)=\frac{2 x^{2}+2}{x^{2}+1}=\frac{2\cancel{\left(x^{2}+1\right)}}{\cancel{\left(x^{2}+1\right)}}=2\)
The following example uses linear functions to model some basic economic relationship
The cost \(\ C\), in dollars, to produce \(\ x\) PortaBoy4 game systems for a local retailer is given by \(\ C(x) = 80x + 150\) for \(\ x ≥ 0\).
- Find and interpret \(\ C(10)\).
- How many PortaBoys can be produced for $15,000?
- Explain the significance of the restriction on the domain, \(\ x ≥ 0\).
- Find and interpret \(\ C(0)\).
- Find and interpret the slope of the graph of \(\ y = C(x)\).
Solution
- To find \(\ C(10)\), we replace every occurrence of \(\ x\) with 10 in the formula for \(\ C(x)\) to get \(\ C(10) = 80(10) + 150 = 950\). Since \(\ x\) represents the number of PortaBoys produced, and \(\ C(x)\) represents the cost, in dollars, \(\ C(10) = 950\) means it costs $950 to produce 10 PortaBoys for the local retailer.
- To find how many PortaBoys can be produced for $15,000, we solve \(\ C(x) = 15000\), or \(\ 80x + 150 = 15000\). Solving, we get \(\ x=\frac{14850}{80}=185.625\). Since we can only produce a whole number amount of PortaBoys, we can produce 185 PortaBoys for $15,000.
- The restriction \(\ x ≥ 0\) is the applied domain, as discussed in Section 1.4.1. In this context, \(\ x\) represents the number of PortaBoys produced. It makes no sense to produce a negative quantity of game systems.5
- We find \(\ C(0) = 80(0) + 150 = 150\). This means it costs $150 to produce 0 PortaBoys. As mentioned on page 82, this is the fixed, or start-up cost of this venture.
- If we were to graph \(\ y = C(x)\), we would be graphing the portion of the line \(\ y = 80x + 150\) for \(\ x ≥ 0\). We recognize the slope, \(\ m = 80\). Like any slope, we can interpret this as a rate of change. Here, \(\ C(x)\) is the cost in dollars, while \(\ x\) measures the number of PortaBoys so
\(\ m=\frac{\Delta y}{\Delta x}=\frac{\Delta C}{\Delta x}=80=\frac{80}{1}=\frac{\$ 80}{1 \text { PortaBoy }}.\)
In other words, the cost is increasing at a rate of $80 per PortaBoy produced. This is often called the variable cost for this venture.
The next example asks us to find a linear function to model a related economic problem.
The local retailer in Example 2.1.5 has determined that the number \(\ x\) of PortaBoy game systems sold in a week is related to the price \(\ p\) in dollars of each system. When the price was $220, 20 game systems were sold in a week. When the systems went on sale the following week, 40 systems were sold at $190 a piece.
- Find a linear function which fits this data. Use the weekly sales \(\ x\) as the independent variable and the price \(\ p\) as the dependent variable.
- Find a suitable applied domain.
- Interpret the slope.
- If the retailer wants to sell 150 PortaBoys next week, what should the price be?
- What would the weekly sales be if the price were set at $150 per system?
Solution
- We recall from Section 1.4 the meaning of ‘independent’ and ‘dependent’ variable. Since \(\ x\) is to be the independent variable, and \(\ p\) the dependent variable, we treat \(\ x\) as the input variable and \(\ p\) as the output variable. Hence, we are looking for a function of the form \(\ p(x) = mx+b\). To determine \(\ m\) and \(\ b\), we use the fact that 20 PortaBoys were sold during the week when the price was 220 dollars and 40 units were sold when the price was 190 dollars. Using function notation, these two facts can be translated as \(\ p(20) = 220\) and \(\ p(40) = 190\). Since \(\ m\) represents the rate of change of \(\ p\) with respect to \(\ x\), we have
\(\ m=\frac{\Delta p}{\Delta x}=\frac{190-220}{40-20}=\frac{-30}{20}=-1.5.\)
We now have determined \(\ p(x) = −1.5x+b\). To determine \(\ b\), we can use our given data again. Using \(\ p(20) = 220\), we substitute \(\ x = 20\) into \(\ p(x) = 1.5x + b\) and set the result equal to 220: \(\ −1.5(20) + b = 220\). Solving, we get \(\ b = 250\). Hence, we get \(\ p(x) = −1.5x + 250\). We can check our formula by computing \(\ p(20)\) and \(\ p(40)\) to see if we get 220 and 190, respectively. You may recall from page 82 that the function \(\ p(x)\) is called the price-demand (or simply demand) function for this venture.
- To determine the applied domain, we look at the physical constraints of the problem. Certainly, we can’t sell a negative number of PortaBoys, so \(\ x ≥ 0\). However, we also note that the slope of this linear function is negative, and as such, the price is decreasing as more units are sold. Thus another constraint on the price is \(\ p(x) ≥ 0\). Solving \(\ −1.5x + 250 ≥ 0\) results in \(\ −1.5x ≥ −250\) or \(\ x \leq \frac{500}{3}=166 . \overline{6}\). Since \(\ x\) represents the number of PortaBoys sold in a week, we round down to 166. As a result, a reasonable applied domain for \(\ p\) is [0, 166].
- The slope \(\ m = −1.5\), once again, represents the rate of change of the price of a system with respect to weekly sales of PortaBoys. Since the slope is negative, we have that the price is decreasing at a rate of $1.50 per PortaBoy sold. (Said differently, you can sell one more PortaBoy for every $1.50 drop in price.)
- To determine the price which will move 150 PortaBoys, we find \(\ p(150) = −1.5(150)+250 = 25\). That is, the price would have to be $25.
- If the price of a PortaBoy were set at $150, we have \(\ p(x) = 150\), or, \(\ −1.5x+250 = 150\). Solving, we get \(\ −1.5x = −100\) or \(\ x=66 . \overline{6}\). This means you would be able to sell 66 PortaBoys a week if the price were $150 per system.
Not all real-world phenomena can be modeled using linear functions. Nevertheless, it is possible to use the concept of slope to help analyze non-linear functions using the following.
Let \(\ f\) be a function defined on the interval \(\ [a, b]\). The average rate of change of \(\ f\) over \(\ [a, b]\) is defined as:
\(\ \frac{\Delta f}{\Delta x}=\frac{f(b)-f(a)}{b-a}\)
Geometrically, if we have the graph of \(\ y = f(x)\), the average rate of change over \(\ [a, b]\) is the slope of the line which connects \(\ (a, f(a))\) and \(\ (b, f(b))\). This is called the secant line through these points. For that reason, some textbooks use the notation \(\ m_{\mathrm{sec}}\) for the average rate of change of a function. Note that for a linear function \(\ m=m_{\mathrm{sec}}\), or in other words, its rate of change over an interval is the same as its average rate of change.
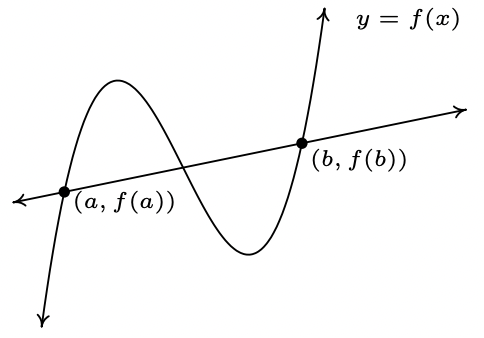 The graph of \(\ y = f(x)\) and its secant line through \(\ (a, f(a))\) and \(\ (b, f(b))\)
The graph of \(\ y = f(x)\) and its secant line through \(\ (a, f(a))\) and \(\ (b, f(b))\)The interested reader may question the adjective ‘average’ in the phrase ‘average rate of change’. In the figure above, we can see that the function changes wildly on \(\ [a, b]\), yet the slope of the secant line only captures a snapshot of the action at \(\ a\) and \(\ b\). This situation is entirely analogous to the average speed on a trip. Suppose it takes you 2 hours to travel 100 miles. Your average speed is \(\ \frac{100 \text { miles }}{2 \text { hours }}=50\) miles per hour. However, it is entirely possible that at the start of your journey, you traveled 25 miles per hour, then sped up to 65 miles per hour, and so forth. The average rate of change is akin to your average speed on the trip. Your speedometer measures your speed at any one instant along the trip, your instantaneous rate of change, and this is one of the central themes of Calculus.6
When interpreting rates of change, we interpret them the same way we did slopes. In the context of functions, it may be helpful to think of the average rate of change as:
\(\ \frac{\text { change in outputs }}{\text { change in inputs }}\)
Recall from page 82, the revenue from selling \(\ x\) units at a price \(\ p\) per unit is given by the formula \(\ R = xp\). Suppose we are in the scenario of Examples 2.1.5 and 2.1.6.
- Find and simplify an expression for the weekly revenue \(\ R(x)\) as a function of weekly sales \(\ x\).
- Find and interpret the average rate of change of \(\ R(x)\) over the interval \(\ [0, 50]\).
- Find and interpret the average rate of change of \(\ R(x)\) as \(\ x\) changes from 50 to 100 and compare that to your result in part 2.
- Find and interpret the average rate of change of weekly revenue as weekly sales increase from 100 PortaBoys to 150 PortaBoys.
Solution
- Since \(\ R = xp\), we substitute \(\ p(x) = −1.5x+ 250\) from Example 2.1.6 to get \(\ R(x)=x(-1.5x +250)=-1.5 x^{2}+250 x\). Since we determined the price-demand function \(\ p(x)\) is restricted to \(\ 0 ≤ x ≤ 166\), \(\ R(x)\) is restricted to these values of x as well.
- Using Definition 2.3, we get that the average rate of change is
\(\ \frac{\Delta R}{\Delta x}=\frac{R(50)-R(0)}{50-0}=\frac{8750-0}{50-0}=175.\)
Interpreting this slope as we have in similar situations, we conclude that for every additional PortaBoy sold during a given week, the weekly revenue increases $175.
- The wording of this part is slightly different than that in Definition 2.3, but its meaning is to find the average rate of change of \(\ R\) over the interval [50, 100]. To find this rate of change, we compute
\(\ \frac{\Delta R}{\Delta x}=\frac{R(100)-R(50)}{100-50}=\frac{10000-8750}{50}=25.\)
In other words, for each additional PortaBoy sold, the revenue increases by $25. Note that while the revenue is still increasing by selling more game systems, we aren’t getting as much of an increase as we did in part 2 of this example. (Can you think of why this would happen?)
- Translating the English to the mathematics, we are being asked to find the average rate of change of \(\ R\) over the interval [100, 150]. We find
\(\ \frac{\Delta R}{\Delta x}=\frac{R(150)-R(100)}{150-100}=\frac{3750-10000}{50}=-125.\)
This means that we are losing $125 dollars of weekly revenue for each additional PortaBoy sold. (Can you think why this is possible?)
We close this section with a new look at difference quotients which were first introduced in Section 1.4. If we wish to compute the average rate of change of a function \(\ f\) over the interval \(\ [x, x + h]\), then we would have
\(\ \frac{\Delta f}{\Delta x}=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}\)
As we have indicated, the rate of change of a function (average or otherwise) is of great importance in Calculus.7 Also, we have the geometric interpretation of difference quotients which was promised to you back on page 81 – a difference quotient yields the slope of a secant line.
2.1.1 Exercises
In Exercises 1 - 10, find both the point-slope form and the slope-intercept form of the line with the given slope which passes through the given point.
- \(\ m = 3, P(3, −1)\)
- \(\ m = −2, P(−5, 8)\)
- \(\ m = −1, P(−7, −1)\)
- \(\ m=\frac{2}{3}, \quad P(-2,1)\)
- \(\ m=-\frac{1}{5}, \quad P(10,4)\)
- \(\ m=\frac{1}{7}, \quad P(-1,4)\)
- \(\ m = 0, P(3, 117)\)
- \(\ m=-\sqrt{2}, \quad P(0,-3)\)
- \(\ m=-5, \quad P(\sqrt{3}, 2 \sqrt{3})\)
- \(\ m = 678, P(−1, −12)\)
In Exercises 11 - 20, find the slope-intercept form of the line which passes through the given points.
- \(\ P(0, 0), Q(−3, 5)\)
- \(\ P(−1, −2), Q(3, −2)\)
- \(\ P(5, 0), Q(0, −8)\)
- \(\ P(3, −5), Q(7, 4)\)
- \(\ P(−1, 5), Q(7, 5)\)
- \(\ P(4, −8), Q(5, −8)\)
- \(\ P\left(\frac{1}{2}, \frac{3}{4}\right), Q\left(\frac{5}{2},-\frac{7}{4}\right)\)
- \(\ P\left(\frac{2}{3}, \frac{7}{2}\right), Q\left(-\frac{1}{3}, \frac{3}{2}\right)\)
- \(\ P(\sqrt{2},-\sqrt{2}), Q(-\sqrt{2}, \sqrt{2})\)
- \(\ P(-\sqrt{3},-1), Q(\sqrt{3}, 1)\)
In Exercises 21 - 26, graph the function. Find the slope, y-intercept and x-intercept, if any exist.
- \(\ f(x)=2 x-1\)
- \(\ f(x)=3-x\)
- \(\ f(x)=3\)
- \(\ f(x)=0\)
- \(\ f(x)=\frac{2}{3} x+\frac{1}{3}\)
- \(\ f(x)=\frac{1-x}{2}\)
- Find all of the points on the line \(\ y = 2x + 1\) which are 4 units from the point (-1, 3).
- Jeff can walk comfortably at 3 miles per hour. Find a linear function \(\ d\) that represents the total distance Jeff can walk in \(\ t\) hours, assuming he doesn’t take any breaks.
- Carl can stuff 6 envelopes per minute. Find a linear function \(\ E\) that represents the total number of envelopes Carl can stuff after t hours, assuming he doesn’t take any breaks.
- A landscaping company charges $45 per cubic yard of mulch plus a delivery charge of $20. Find a linear function which computes the total cost \(\ C\) (in dollars) to deliver \(\ x\) cubic yards of much.
- A plumber charges $50 for a service call plus $80 per hour. If she spends no longer than 8 hours a day at any one site, find a linear function that represents her total daily charges \(\ C\) (in dollars) as a function of time \(\ t\) (in hours) spent at any one given location.
- A salesperson is paid $200 per week plus 5% commission on her weekly sales of \(\ x\) dollars. Find a linear function that represents her total weekly pay, \(\ W\) (in dollars) in terms of \(\ x\). What must her weekly sales be in order for her to earn $475.00 for the week?
- 33. An on-demand publisher charges $22.50 to print a 600 page book and $15.50 to print a 400 page book. Find a linear function which models the cost of a book \(\ C\) as a function of the number of pages \(\ p\). Interpret the slope of the linear function and find and interpret \(\ C(0)\).
- The Topology Taxi Company charges $2.50 for the first fifth of a mile and $0.45 for each additional fifth of a mile. Find a linear function which models the taxi fare \(\ F\) as a function of the number of miles driven, \(\ m\). Interpret the slope of the linear function and find and interpret \(\ F(0)\).
- Water freezes at \(\ 0^{\circ}\) Celsius and \(\ 32^{\circ}\) Fahrenheit and it boils at \(\ 100^{\circ} \mathrm{C}\) and \(\ 212^{\circ} \mathrm{F}\).
- Find a linear function \(\ F\) that expresses temperature in the Fahrenheit scale in terms of degrees Celsius. Use this function to convert \(\ 20^{\circ} \mathrm{C}\) into Fahrenheit.
- Find a linear function \(\ C\) that expresses temperature in the Celsius scale in terms of degrees Fahrenheit. Use this function to convert \(\ 110^{\circ} \mathrm{F}\) into Celsius.
- Is there a temperature n such that \(\ F(n) = C(n)\)?
- Legend has it that a bull Sasquatch in rut will howl approximately 9 times per hour when it is \(\ 40^{\circ} \mathrm{F}\) outside and only 5 times per hour if it’s \(\ 70^{\circ} \mathrm{F}\). Assuming that the number of howls per hour, \(\ N\), can be represented by a linear function of temperature Fahrenheit, find the number of howls per hour he’ll make when it’s only \(\ 20^{\circ} \mathrm{F}\) outside. What is the applied domain of this function? Why?
- Economic forces beyond anyone’s control have changed the cost function for PortaBoys to \(\ C(x) = 105x + 175\). Rework Example 2.1.5 with this new cost function.
- In response to the economic forces in Exercise 37 above, the local retailer sets the selling price of a PortaBoy at $250. Remarkably, 30 units were sold each week. When the systems went on sale for $220, 40 units per week were sold. Rework Examples 2.1.6 and 2.1.7 with this new data. What difficulties do you encounter?
- A local pizza store offers medium two-topping pizzas delivered for $6.00 per pizza plus a $1.50 delivery charge per order. On weekends, the store runs a ‘game day’ special: if six or more medium two-topping pizzas are ordered, they are $5.50 each with no delivery charge. Write a piecewise-defined linear function which calculates the cost \(\ C\) (in dollars) of \(\ p\) medium two-topping pizzas delivered during a weekend.
- A restaurant offers a buffet which costs $15 per person. For parties of 10 or more people, a group discount applies, and the cost is $12.50 per person. Write a piecewise-defined linear function which calculates the total bill \(\ T\) of a party of \(\ n\) people who all choose the buffet.
- A mobile plan charges a base monthly rate of $10 for the first 500 minutes of air time plus a charge of 15¢ for each additional minute. Write a piecewise-defined linear function which calculates the monthly cost \(\ C\) (in dollars) for using \(\ m\) minutes of air time.
HINT: You may want to revisit Exercise 74 in Section 1.4
- The local pet shop charges 12¢ per cricket up to 100 crickets, and 10¢ per cricket thereafter. Write a piecewise-defined linear function which calculates the price \(\ P\), in dollars, of purchasing \(\ c\) crickets.
- The cross-section of a swimming pool is below. Write a piecewise-defined linear function which describes the depth of the pool, \(\ D\) (in feet) as a function of:
- the distance (in feet) from the edge of the shallow end of the pool, d.
- the distance (in feet) from the edge of the deep end of the pool, \(\ s\).
- Graph each of the functions in (a) and (b). Discuss with your classmates how to transform one into the other and how they relate to the diagram of the pool.
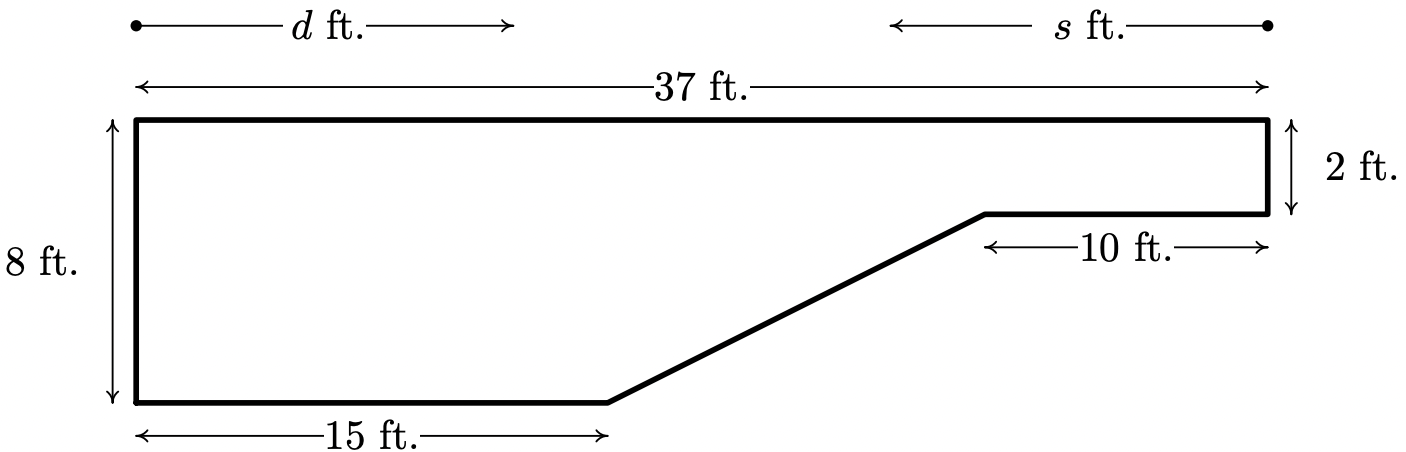
In Exercises 44 - 49, compute the average rate of change of the function over the specified interval.
- \(\ f(x)=x^{3},[-1,2]\)
- \(\ f(x)=\frac{1}{x},[1,5]\)
- \(\ f(x)=\sqrt{x},[0,16]\)
- \(\ f(x)=x^{2},[-3,3]\)
- \(\ f(x)=\frac{x+4}{x-3},[5,7]\)
- \(\ f(x)=3 x^{2}+2 x-7,[-4,2]\)
In Exercises 50 - 53, compute the average rate of change of the given function over the interval \(\ [x, x + h]\). Here we assume \(\ [x, x + h]\) is in the domain of the function.
- \(\ f(x)=x^{3}\)
- \(\ f(x)=\frac{1}{x}\)
- \(\ f(x)=\frac{x+4}{x-3}\)
- \(\ f(x)=3 x^{2}+2 x-7\)
- The height of an object dropped from the roof of an eight story building is modeled by: \(\ h(t)=-16 t^{2}+64,0 \leq t \leq 2\). Here, \(\ h\) is the height of the object off the ground in feet, \(\ t\) seconds after the object is dropped. Find and interpret the average rate of change of \(\ h\) over the interval [0, 2].
- Using data from Bureau of Transportation Statistics, the average fuel economy \(\ F\) in miles per gallon for passenger cars in the US can be modeled by \(\ F(t)=-0.0076 t^{2}+0.45 t+16\), \(\ 0 ≤ t ≤ 28\), where \(\ t\) is the number of years since 1980. Find and interpret the average rate of change of \(\ F\) over the interval [0, 28].
- The temperature \(\ T\) in degrees Fahrenheit \(\ t\) hours after 6 AM is given by:
\(\ T(t)=-\frac{1}{2} t^{2}+8 t+32, \quad 0 \leq t \leq 12\)
- Find and interpret \(\ T(4)\), \(\ T(8)\) and \(\ T(12)\).
- Find and interpret the average rate of change of \(\ T\) over the interval [4, 8].
- Find and interpret the average rate of change of \(\ T\) from \(\ t = 8\) to \(\ t = 12\).
- Find and interpret the average rate of temperature change between 10 AM and 6 PM.
- Suppose \(\ C(x)=x^{2}-10 x+27\) represents the costs, in hundreds, to produce \(\ x\) thousand pens. Find and interpret the average rate of change as production is increased from making 3000 to 5000 pens.
- With the help of your classmates find several other “real-world” examples of rates of change that are used to describe non-linear phenomena.
(Parallel Lines) Recall from Intermediate Algebra that parallel lines have the same slope. (Please note that two vertical lines are also parallel to one another even though they have an undefined slope.) In Exercises 59 - 64, you are given a line and a point which is not on that line. Find the line parallel to the given line which passes through the given point.
- \(\ y = 3x + 2, P(0, 0) \)
- \(\ y = −6x + 5, P(3, 2)\)
- \(\ y=\frac{2}{3} x-7, P(6,0)\)
- \(\ y=\frac{4-x}{3}, P(1,-1)\)
- \(\ y = 6, P(3, −2)\)
- \(\ x = 1, P(−5, 0)\)
(Perpendicular Lines) Recall from Intermediate Algebra that two non-vertical lines are perpendicular if and only if they have negative reciprocal slopes. That is to say, if one line has slope \(\ m_{1}\) and the other has slope \(\ m_{2}\) then \(\ m_{1} \cdot m_{2}=-1\). (You will be guided through a proof of this result in Exercise 71.) Please note that a horizontal line is perpendicular to a vertical line and vice versa, so we assume \(\ m_{1} \neq 0\) and \(\ m_{2} \neq 0\). In Exercises 65 - 70, you are given a line and a point which is not on that line. Find the line perpendicular to the given line which passes through the given point.
- \(\ y=\frac{1}{3} x+2, P(0,0)\)
- \(\ y=-6 x+5, P(3,2)\)
- \(\ y=\frac{2}{3} x-7, P(6,0)\)
- \(\ y=\frac{4-x}{3}, P(1,-1)\)
- \(\ y = 6, P(3, −2)\)
- \(\ x = 1, P(−5, 0)\)
- We shall now prove that \(\ y=m_{1} x+b_{1}\) is perpendicular to \(\ y=m_{2} x+b_{2}\) if and only if \(\ m_{1} \cdot m_{2}=-1\). To make our lives easier we shall assume that \(\ m_{1}>0\) and \(\ m_{2}<0\). We can also “move” the lines so that their point of intersection is the origin without messing things up, so we’ll assume \(\ b_{1}=b_{2}=0\). (Take a moment with your classmates to discuss why this is okay.) Graphing the lines and plotting the points \(\ O(0, 0)\), \(\ P\left(1, m_{1}\right)\) and \(\ Q\left(1, m_{2}\right)\) gives us the following set up.
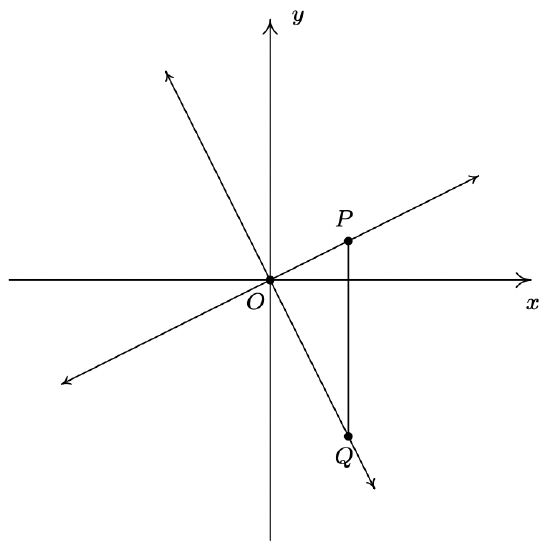
The line \(\ y=m_{1} x\) will be perpendicular to the line \(\ y=m_{2} x\) if and only if \(\ \triangle O P Q\) is a right triangle. Let \(\ d_{1}\) be the distance from \(\ O\) to \(\ P\), let \(\ d_{2}\) be the distance from \(\ O\) to \(\ Q\) and let \(\ d_{3}\) be the distance from \(\ P\) to \(\ Q\). Use the Pythagorean Theorem to show that \(\ \triangle O P Q\) is a right triangle if and only if \(\ m_{1} \cdot m_{2}=-1\) by showing \(\ d_{1}^{2}+d_{2}^{2}=d_{3}^{2}\) if and only if \(\ m_{1} \cdot m_{2}=-1\).
- Show that if \(\ a \neq b\), the line containing the points \(\ (a, b)\) and \(\ (b, a)\) is perpendicular to the line \(\ y = x\). (Coupled with the result from Example 1.1.7 on page 13, we have now shown that the line \(\ y = x\) is a perpendicular bisector of the line segment connecting \(\ (a, b)\) and \(\ (b, a)\). This means the points \(\ (a, b)\) and \(\ (b, a)\) are symmetric about the line \(\ y = x\). We will revisit this symmetry in section 5.2.)
- The function defined by \(\ I(x) = x\) is called the Identity Function.
- Discuss with your classmates why this name makes sense.
- Show that the point-slope form of a line (Equation 2.2) can be obtained from \(\ I\) using a sequence of the transformations defined in Section 1.7.
2.1.2 Answers
- \(\ \begin{aligned}
&y+1=3(x-3) \\
&y=3 x-10
\end{aligned}\) - \(\ \begin{aligned}
&y-8=-2(x+5) \\
&y=-2 x-2
\end{aligned}\) - \(\ \begin{aligned}
&y+1=-(x+7) \\
&y=-x-8
\end{aligned}\) - \(\ \begin{aligned}
&y-1=\frac{2}{3}(x+2) \\
&y=\frac{2}{3} x+\frac{7}{3}
\end{aligned}\) - \(\ \begin{aligned}
&y-4=-\frac{1}{5}(x-10) \\
&y=-\frac{1}{5} x+6
\end{aligned}\) - \(\ \begin{aligned}
&y-4=\frac{1}{7}(x+1) \\
&y=\frac{1}{7} x+\frac{29}{7}
\end{aligned}\) - \(\ \begin{aligned}
&y-117=0 \\
&y=117
\end{aligned}\) - \(\ \begin{aligned}
&y+3=-\sqrt{2}(x-0) \\
&y=-\sqrt{2} x-3
\end{aligned}\) - \(\ \begin{aligned}
&y-2 \sqrt{3}=-5(x-\sqrt{3}) \\
&y=-5 x+7 \sqrt{3}
\end{aligned}\) - \(\ \begin{aligned}
&y+12=678(x+1) \\
&y=678 x+666
\end{aligned}\) - \(\ y=-\frac{5}{3} x\)
- \(\ y = −2\)
- \(\ y=\frac{8}{5} x-8\)
- \(\ y=\frac{9}{4} x-\frac{47}{4}\)
- \(\ y = 5\)
- \(\ y = −8\)
- \(\ y=-\frac{5}{4} x+\frac{11}{8}\)
- \(\ y=2 x+\frac{13}{6}\)
- \(\ y = −x\)
- \(\ y=\frac{\sqrt{3}}{3} x\)
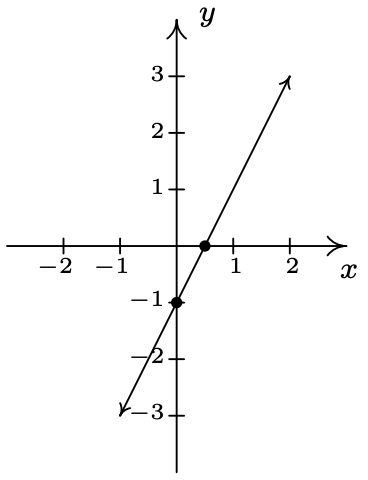
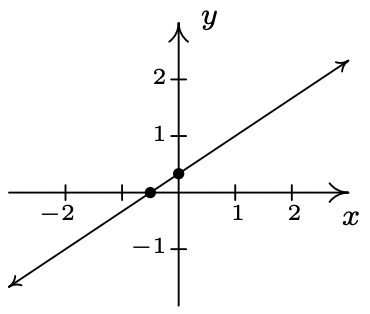
- \(\ f(x) = 2x − 1\)
slope: \(\ m = 2\)
y-intercept: (0, −1)
x-intercept: \(\ \left(\frac{1}{2}, 0\right)\)
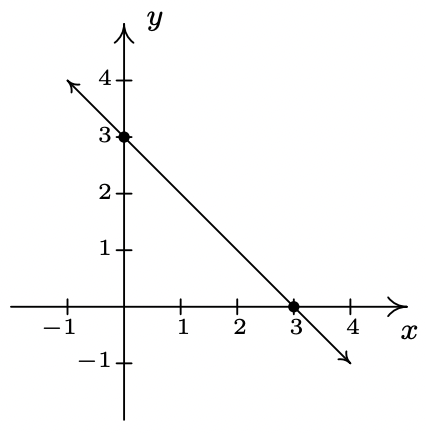
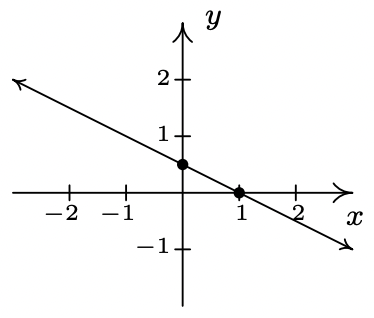
- \(\ f(x) = 3 − x\)
slope: \(\ m = − 1\)
y-intercept: (0, 3)
x-intercept: (3, 0)
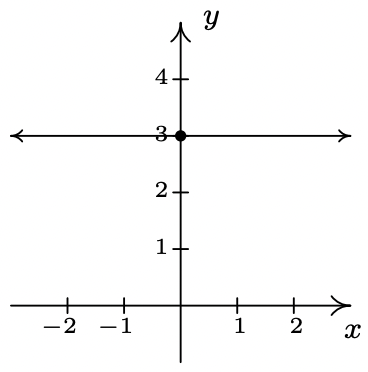
- \(\ f(x) = 3\)
slope: \(\ m = 0\)
y-intercept: (0, 3)
x-intercept: none
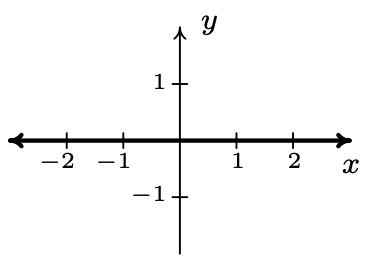
- f(x) = 0
slope: \(\ m = 0\)
y-intercept: (0, 0)
x-intercept: \(\ \{(x, 0)| x\) is a real number\(\ \}\)
- \(\ f(x)=\frac{2}{3} x+\frac{1}{3}\)
slope: \(\ m=\frac{2}{3}\)
y-intercept: \(\ \left(0, \frac{1}{3}\right)\)
x-intercept: \(\ \left(-\frac{1}{2}, 0\right)\)
- \(\ f(x)=\frac{1-x}{2}\)
slope: \(\ m=-\frac{1}{2}\)
y-intercept: \(\ \left(0, \frac{1}{2}\right)\)
x-intercept: \(\ (1,0)\)
- \(\ (-1,-1) \text { and }\left(\frac{11}{5}, \frac{27}{5}\right)\)
- \(\ d(t)=3 t, t \geq 0\)
- \(\ E(t)=360 t, t \geq 0\)
- \(\ C(x)=45 x+20, x \geq 0\)
- \(\ C(t)=80 t+50,0 \leq t \leq 8\)
- \(\ W(x)=200+.05 x, x \geq 0\) She must make $5500 in weekly sales
- \(\ C(p)=0.035 p+1.5\) The slope 0.035 means it costs 3.5¢ per page. \(\ C(0) = 1.5\) means there is a fixed, or start-up, cost of $1.50 to make each book.
- \(\ F(m) = 2.25m+ 2.05\) The slope 2.25 means it costs an additional $2.25 for each mile beyond the first 0.2 miles. \(\ F(0) = 2.05\), so according to the model, it would cost $2.05 for a trip of 0 miles. Would this ever really happen? Depends on the driver and the passenger, we suppose.
-
- \(\ F(C)=\frac{9}{5} C+32\)
- \(\ C(F)=\frac{5}{9}(F-32)=\frac{5}{9} F-\frac{160}{9}\)
- \(\ F(−40) = −40 = C(−40)\)
- \(\ N(T)=-\frac{2}{15} T+\frac{43}{3} \text { and } N(20)=\frac{35}{3} \approx 12 \text { howls per hour }\)
Having a negative number of howls makes no sense and since \(\ N(107.5) = 0\) we can put an upper bound of \(\ 107.5^{\circ} \mathrm{F}\) on the domain. The lower bound is trickier because there’s nothing other than common sense to go on. As it gets colder, he howls more often. At some point it will either be so cold that he freezes to death or he’s howling non-stop. So we’re going to say that he can withstand temperatures no lower than \(\ -60^{\circ} \mathrm{F}\) so that the applied domain is [−60, 107.5].
- \(\ C(p)=\left\{\begin{array}{rll}
6 p+1.5 & \text { if } & 1 \leq p \leq 5 \\
5.5 p & \text { if } & p \geq 6
\end{array}\right.\) - \(\ T(n)=\left\{\begin{array}{rll}
15 n & \text { if } & 1 \leq n \leq 9 \\
12.5 n & \text { if } & n \geq 10
\end{array}\right.\) - \(\ C(m)=\left\{\begin{array}{rll}
10 & \text { if } & 0 \leq m \leq 500 \\
10+0.15(m-500) & \text { if } & m>500
\end{array}\right.\) - \(\ P(c)=\left\{\begin{array}{rll}
0.12 c & \text { if } & 1 \leq c \leq 100 \\
12+0.1(c-100) & \text { if } & c>100
\end{array}\right.\) -
- \(\ D(d)=\left\{\begin{array}{rll}
8 & \text { if } & 0 \leq d \leq 15 \\
-\frac{1}{2} d+\frac{31}{2} & \text { if } & 15 \leq d \leq 27 \\
2 & \text { if } & 27 \leq d \leq 37
\end{array}\right.\) - \(\ D(s)=\left\{\begin{array}{rll}
2 & \text { if } & 0 \leq s \leq 10 \\
\frac{1}{2} s-3 & \text { if } & 10 \leq s \leq 22 \\
8 & \text { if } & 22 \leq s \leq 37
\end{array}\right.\) 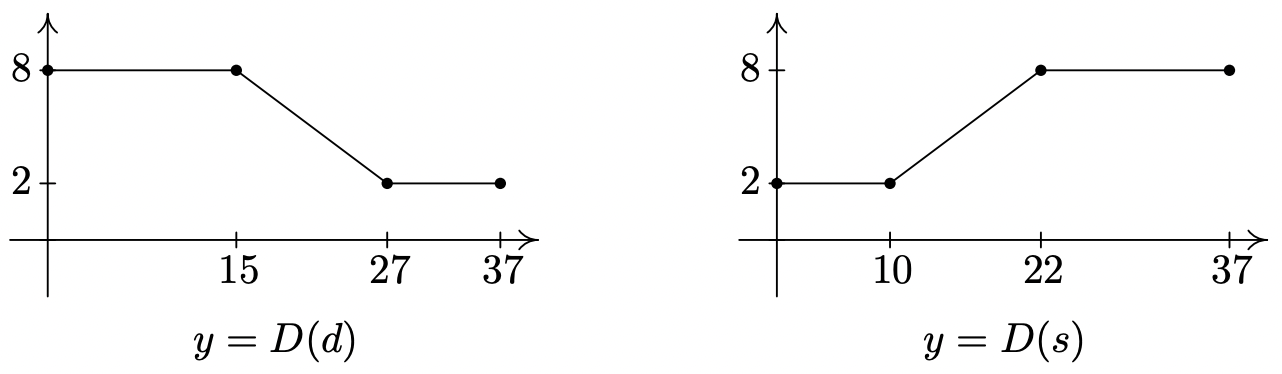
- \(\ D(d)=\left\{\begin{array}{rll}
- \(\ \frac{2^{3}-(-1)^{3}}{2-(-1)}=3\)
- \(\ \frac{\frac{1}{5}-\frac{1}{1}}{5-1}=-\frac{1}{5}\)
- \(\ \frac{\sqrt{16}-\sqrt{0}}{16-0}=\frac{1}{4}\)
- \(\ \frac{3^{2}-(-3)^{2}}{3-(-3)}=0\)
- \(\ \frac{\frac{7+4}{7-3}-\frac{5+4}{5-3}}{7-5}=-\frac{7}{8}\)
- \(\ \frac{\left(3(2)^{2}+2(2)-7\right)-\left(3(-4)^{2}+2(-4)-7\right)}{2-(-4)}=-4\)
- \(\ 3 x^{2}+3 x h+h^{2}\)
- \(\ \frac{-1}{x(x+h)}\)
- \(\ \frac{-7}{(x-3)(x+h-3)}\)
- \(\ 6 x+3 h+2\)
- The average rate of change is \(\ \frac{h(2)-h(0)}{2-0}=-32\). During the first two seconds after it is dropped, the object has fallen at an average rate of 32 feet per second. (This is called the average velocity of the object.)
- The average rate of change is \(\ \frac{F(28)-F(0)}{28-0}=0.2372\). During the years from 1980 to 2008, the average fuel economy of passenger cars in the US increased, on average, at a rate of 0.2372 miles per gallon per year.
-
- \(\ T(4) = 56\), so at 10 AM (4 hours after 6 AM), it is \(\ 56^{\circ} \mathrm{F}\). \(\ T(8) = 64\), so at 2 PM (8 hours after 6 AM), it is \(\ 64^{\circ} \mathrm{F}\). \(\ T(12) = 56\), so at 6 PM (12 hours after 6 AM), it is \(\ 56^{\circ} \mathrm{F}\).
- The average rate of change is \(\ \frac{T(8)-T(4)}{8-4}=2\). Between 10 AM and 2 PM, the temperature increases, on average, at a rate of \(\ 2^{\circ} \mathrm{F}\) per hour.
- The average rate of change is \(\ \frac{T(12)-T(8)}{12-8}=-2\). Between 2 PM and 6 PM, the temperature decreases, on average, at a rate of \(\ 2^{\circ} \mathrm{F}\) per hour.
- The average rate of change is \(\ \frac{T(12)-T(4)}{12-4}=0\). Between 10 AM and 6 PM, the temperature, on average, remains constant.
- The average rate of change is \(\ \frac{C(5)-C(3)}{5-3}=-2\). As production is increased from 3000 to 5000 pens, the cost decreases at an average rate of $200 per 1000 pens produced (20¢ per pen.)
- \(\ y = 3x\)
- \(\ y = −6x + 20\)
- \(\ y=\frac{2}{3} x-4\)
- \(\ y=-\frac{1}{3} x-\frac{2}{3}\)
- \(\ y = −2\)
- \(\ x = −5\)
- \(\ y = −3x\)
- \(\ y=\frac{1}{6} x+\frac{3}{2}\)
- \(\ y=-\frac{3}{2} x+9\)
- \(\ y = 3x − 4\)
- \(\ x = 3\)
- \(\ y = 0\)
Reference
1 See www.mathforum.org or www.mathworld.wolfram.com for discussions on this topic.
2 Some authors use the unfortunate moniker ‘no slope’ when a slope is undefined. It’s easy to confuse the notions of ‘no slope’ with ‘slope of 0’. For this reason, we will describe slopes of vertical lines as ‘undefined’.
3 We can also understand this equation in terms of applying transformations to the function \(\ I(x) = x\). See the Exercises.
4 The similarity of this name to PortaJohn is deliberate.
5 Actually, it makes no sense to produce a fractional part of a game system, either, as we saw in the previous part of this example. This absurdity, however, seems quite forgivable in some textbooks but not to us.
6 Here we go again...
7 So we are not torturing you with these for nothing.


