11.7: Polar Form of Complex Numbers
- Page ID
- 80832
In this section, we return to our study of complex numbers which were first introduced in Section 3.4. Recall that a complex number is a number of the form \(z=a+b i\) where a and b are real numbers and i is the imaginary unit defined by \(i=\sqrt{-1}\). The number \(a\) is called the real part of \(z\), denoted Re(\(z\)), while the real number \(b\) is called the imaginary part of \(z\), denoted Im(\(z\)). From Intermediate Algebra, we know that if \(z = a + bi = c + di\) where \(a, b, c\) and \(d\) are real numbers, then \(a = c\) and \(b = d\), which means Re(\(z\)) and Im(\(z\)) are well-defined.1 To start off this section, we associate each complex number \(z = a + bi\) with the point (\(a, b\)) on the coordinate plane. In this case, the \(x\)-axis is relabeled as the real axis, which corresponds to the real number line as usual, and the \(y\)-axis is relabeled as the imaginary axis, which is demarcated in increments of the imaginary unit \(i\). The plane determined by these two axes is called the complex plane.
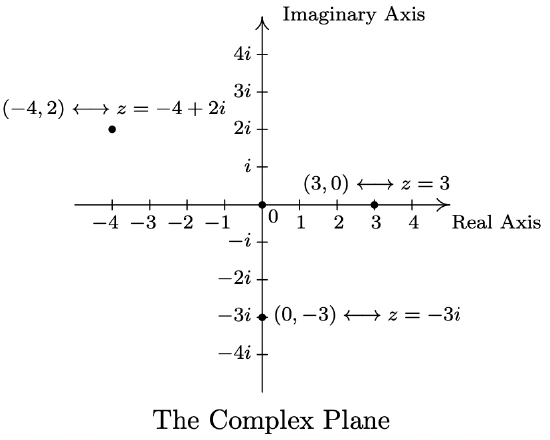
Since the ordered pair \((a, b)\) gives the rectangular coordinates associated with the complex number \(z = a + bi\), the expression \(z = a + bi\) is called the rectangular form of \(z\). Of course, we could just as easily associate \(z\) with a pair of polar coordinates \((r, \theta)\). Although it is not as straightforward as the definitions of Re(\(z\)) and Im(\(z\)), we can still give \(r\) and \(\theta\) special names in relation to \(z\).
Let \(z = a + bi\) be a complex number with \(a\) = Re(\(z\)) and \(b\) = Im(\(z\)). Let \((r, \theta)\) be a polar representation of the point with rectangular coordinates (\(a, b\)) where \(r \geq 0\).
- The modulus of \(z\), denoted \(|z|\), is defined by \(|z| = r\).
- The angle \(\theta\) is an argument of \(z\). The set of all arguments of \(z\) is denoted arg(\(z\)).
- If \(z \neq 0\) and \(-\pi<\theta \leq \pi\), then \(\theta\) is the principal argument of \(z\), written \(\theta=\operatorname{Arg}(z)\).
Some remarks about Definition 11.2 are in order. We know from Section 11.4 that every point in the plane has infinitely many polar coordinate representations \((r, \theta)\) which means it’s worth our time to make sure the quantities ‘modulus’, ‘argument’ and ‘principal argument’ are well-defined. Concerning the modulus, if \(z = 0\) then the point associated with \(z\) is the origin. In this case, the only \(r\)-value which can be used here is \(r = 0\). Hence for \(z = 0\), \(|z| = 0\) is well-defined. If \(z \neq 0\), then the point associated with \(z\) is not the origin, and there are two possibilities for \(r\): one positive and one negative. However, we stipulated \(r \geq 0\) in our definition so this pins down the value of \(|z|\) to one and only one number. Thus the modulus is well-defined in this case, too.2 Even with the requirement \(r \geq 0\), there are infinitely many angles \(\theta\) which can be used in a polar representation of a point \((r, \theta)\). If \(z \neq 0\) then the point in question is not the origin, so all of these angles \(\theta\) are coterminal. Since coterminal angles are exactly \(2 \pi\) radians apart, we are guaranteed that only one of them lies in the interval \((-\pi, \pi]\), and this angle is what we call the principal argument of \(z\), \(\operatorname{Arg}(z)\). In fact, the set \(\arg (z)\) of all arguments of \(z\) can be described using set-builder notation as \(\arg (z)=\{\operatorname{Arg}(z)+2 \pi k \mid k \text { is an integer }\}\). Note that since \(\arg (z)\) is a set, we will write \('\theta \in \arg (z)’\) to mean '\(\theta\) is in3 the set of arguments of \(z\)'. If \(z = 0\) then the point in question is the origin, which we know can be represented in polar coordinates as \((0, \theta)\) for any angle \(\theta\). In this case, we have \(\arg (0)=(-\infty, \infty)\) and since there is no one value of \(\theta\) which lies \((-\pi, \pi]\), we leave \(\operatorname{Arg}(0)\) undefined.4 It is time for an example.
For each of the following complex numbers find \(\operatorname{Re}(z), \operatorname{Im}(z),|z|, \arg (z)\) and \(\operatorname{Arg}(z)\). Plot \(z\) in the complex plane.
- \(z=\sqrt{3}-i\)
- \(z=-2+4 i\)
- \(z = 3i\)
- \(z = −117\)
Solution
- For \(z=\sqrt{3}-i=\sqrt{3}+(-1) i\), we have \(\operatorname{Re}(z)=\sqrt{3}\) and \(\operatorname{Im}(z)=-1\). To find \(|z|, \arg (z)\) and \(\operatorname{Arg}(z)\), we need to find a polar representation \((r, \theta)\) with \(r \geq 0\) for the point \(P(\sqrt{3},-1)\) associated with \(z\). We know \(r^{2}=(\sqrt{3})^{2}+(-1)^{2}=4\), so \(r=\pm 2\). Since we require \(r \geq 0\), we choose \(r = 2\), so \(|z| = 2\). Next, we find a corresponding angle \(\theta\). Since \(r > 0\) and \(P\) lies in Quadrant IV, \(\theta\) is a Quadrant IV angle. We know \(\tan (\theta)=\frac{-1}{\sqrt{3}}=-\frac{\sqrt{3}}{3}\), so \(\theta=-\frac{\pi}{6}+2 \pi k\) for integers \(k\). Hence, \(\arg (z)=\left\{-\frac{\pi}{6}+2 \pi k \mid k \text { is an integer }\right\}\). Of these values, only \(\theta=-\frac{\pi}{6}\) satisfies the requirement that \(-\pi<\theta \leq \pi\), hence \(\operatorname{Arg}(z)=-\frac{\pi}{6}\).
- The complex number \(z = −2 + 4i\) has \(\operatorname{Re}(z)=-2, \operatorname{Im}(z)=4\), and is associated with the point \(P(−2, 4)\). Our next task is to find a polar representation for \(P\) where \(r \geq 0\). Running through the usual calculations gives \(r=2 \sqrt{5}\), so \(|z|=2 \sqrt{5}\). To find \(\theta\), we get \(\tan (\theta)=-2\), and since \(r > 0\) and \(P\) lies in Quadrant II, we know \(\theta\) is a Quadrant II angle. We find \(\theta=\pi+\arctan (-2)+2 \pi k\), or, more succinctly \(\theta=\pi-\arctan (2)+2 \pi k\) for integers \(k\). Hence \(\arg (z)=\{\pi-\arctan (2)+2 \pi k \mid k \text { is an integer }\}\). Only \(\theta=\pi-\arctan (2)\) satisfies the requirement \(-\pi<\theta \leq \pi\), so \(\operatorname{Arg}(z)=\pi-\arctan (2)\).
- We rewrite \(z = 3i as z = 0 + 3i\) to find \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)=3\). The point in the plane which corresponds to \(z\) is (0, 3) and while we could go through the usual calculations to find the required polar form of this point, we can almost ‘see’ the answer. The point (0, 3) lies 3 units away from the origin on the positive \(y\)-axis. Hence, \(r=|z|=3\) and \(\theta=\frac{\pi}{2}+2 \pi k\) for integers \(k\). We get \(\arg (z)=\left\{\frac{\pi}{2}+2 \pi k \mid k \text { is an integer }\right\}\) and \(\operatorname{Arg}(z)=\frac{\pi}{2}\).
- As in the previous problem, we write \(z = −117 = −117 + 0i\) so \(\operatorname{Re}(z)=-117\) and \(\operatorname{Im}(z)=0\). The number \(z = −117\) corresponds to the point (−117, 0), and this is another instance where we can determine the polar form ‘by eye’. The point (−117, 0) is 117 units away from the origin along the negative \(x\)-axis. Hence, \(r = |z| = 117\) and \(\theta=\pi+2 \pi=(2 k+1) \pi k\) for integers \(k\). We have \(\arg (z)=\{(2 k+1) \pi \mid k \text { is an integer}\}\). Only one of these values, \(\theta=\pi\), just barely lies in the interval \((-\pi, \pi]\) which means and \(\operatorname{Arg}(z)=\pi\). We plot \(z\) along with the other numbers in this example below.
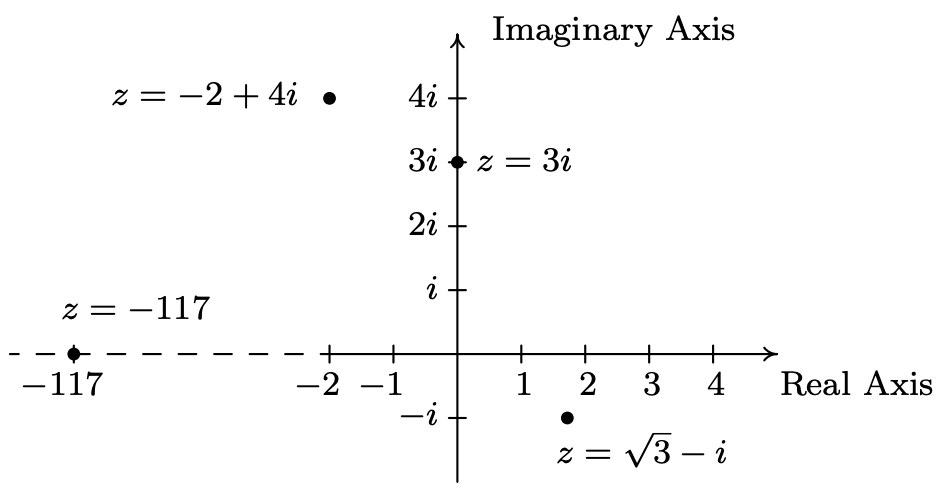
Now that we’ve had some practice computing the modulus and argument of some complex numbers, it is time to explore their properties. We have the following theorem.
Let \(z\) and \(w\) be complex numbers.
- \(|z|\) is the distance from \(z\) to 0 in the complex plane
- \(|z| \geq 0\) and \(|z| = 0\) if and only if \(z = 0\)
- \(|z|=\sqrt{\operatorname{Re}(z)^{2}+\operatorname{Im}(z)^{2}}\)
- Product Rule: \(|z w|=|z||w|\)
- Power Rule: \(\left|z^{n}\right|=|z|^{n}\) for all natural numbers, \(n\)
- Quotient Rule: \(\left|\frac{z}{w}\right|=\frac{|z|}{|w|}\), provided \(w \neq 0\)
To prove the first three properties in Theorem 11.14, suppose \(z = a + bi\) where \(a\) and \(b\) are real numbers. To determine \(|z|\), we find a polar representation \((r, \theta)\) with \(r \geq 0\) for the point \((a, b)\). From Section 11.4, we know \(r^{2}=a^{2}+b^{2}\) so that \(r=\pm \sqrt{a^{2}+b^{2}}\). Since we require \(r \geq 0\), then it must be that \(r=\sqrt{a^{2}+b^{2}}\), which means \(|z|=\sqrt{a^{2}+b^{2}}\). Using the distance formula, we find the distance from (0, 0) to (a, b) is also \(\sqrt{a^{2}+b^{2}}\), establishing the first property.5 For the second property, note that since \(|z|\) is a distance, \(|z| \geq 0\). Furthermore, \(|z| = 0\) if and only if the distance from \(z\) to 0 is 0, and the latter happens if and only if \(z = 0\), which is what we were asked to show.6 For the third property, we note that since \(a=\operatorname{Re}(z)\) and \(b=\operatorname{Im}(z), z=\sqrt{a^{2}+b^{2}}=\sqrt{\operatorname{Re}(z)^{2}+\operatorname{Im}(z)^{2}}\).
To prove the product rule, suppose \(z = a + bi\) and \(w = c + di\) for real numbers \(a, b, c\) and \(d\). Then \(zw = (a + bi)(c + di)\). After the usual arithmetic7 we get \(zw = (ac − bd) + (ad + bc)i\). Therefore,
\(\begin{aligned}
|z w| &=\sqrt{(a c-b d)^{2}+(a d+b c)^{2}} & \\
&=\sqrt{a^{2} c^{2}-2 a b c d+b^{2} d^{2}+a^{2} d^{2}+2 a b c d+b^{2} c^{2}} & & \text { Expand } \\
&=\sqrt{a^{2} c^{2}+a^{2} d^{2}+b^{2} c^{2}+b^{2} d^{2}} & & \text { Rearrange terms } \\
&=\sqrt{a^{2}\left(c^{2}+d^{2}\right)+b^{2}\left(c^{2}+d^{2}\right)} & & \text { Factor } \\
&=\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)} & & \text { Factor } \\
&=\sqrt{a^{2}+b^{2}} \sqrt{c^{2}+d^{2}} & & \text { Product Rule for Radicals } \\
&=|z||w| & & \text { Definition of }|z| \text { and }|w|
\end{aligned}\)
Hence \(|zw| = |z||w|\) as required.
Now that the Product Rule has been established, we use it and the Principle of Mathematical Induction8 to prove the power rule. Let \(P(n)\) be the statement \(\left|z^{n}\right|=|z|^{n}\). Then \(P(1)\) is true since \(\left|z^{1}\right|=|z|=|z|^{1}\). Next, assume \(P(k)\) is true. That is, assume \(\left|z^{k}\right|=|z|^{k}\) for some \(k \geq 1\). Our job is to show that \(P(k + 1)\) is true, namely \(\left|z^{k+1}\right|=|z|^{k+1}\). As is customary with induction proofs, we first try to reduce the problem in such a way as to use the Induction Hypothesis.
\[\begin{array}{rll}
\left|z^{k+1}\right| & =\left|z^{k} z\right| \quad & \text { Properties of Exponents } \\
& =\left|z^{k}\right| z \mid & \text { Product Rule } \\
& =|z|^{k}|z| & \text { Induction Hypothesis } \\
& =|z|^{k+1} & \text { Properties of Exponents }
\end{array}\nonumber\]
Hence, \(P(k + 1)\) is true, which means \(\left|z^{n}\right|=|z|^{n}\) is true for all natural numbers \(n\).
Like the Power Rule, the Quotient Rule can also be established with the help of the Product Rule.
We assume \(w \neq 0\) (so \(|w| \neq 0\)) and we get
\[\begin{aligned}
\left|\frac{z}{w}\right| &=\left|(z)\left(\frac{1}{w}\right)\right| \\
&=|z|\left|\frac{1}{w}\right| \quad \text { Product Rule. }
\end{aligned}\nonumber\]
Hence, the proof really boils down to showing \(\left|\frac{1}{w}\right|=\frac{1}{|w|}\). This is left as an exercise.
Next, we characterize the argument of a complex number in terms of its real and imaginary parts.
Let \(z\) be a complex number.
- If \(\operatorname{Re}(z) \neq 0\) and \(\theta \in \arg (z)\), then \(\tan (\theta)=\frac{\operatorname{Im}(z)}{\operatorname{Re}(z)}\).
- If \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)>0\), then \(\arg (z)=\left\{\frac{\pi}{2}+2 \pi k \mid k \text { is an integer }\right\}\).
- If \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)<0\), then \(\arg (z)=\left\{-\frac{\pi}{2}+2 \pi k \mid k \text { is an integer }\right\}\).
- If \(\operatorname{Re}(z)=\operatorname{Im}(z)=0\), then \(z = 0\) and \(\arg (z)=(-\infty, \infty)\).
To prove Theorem 11.15, suppose \(z = a+bi\) for real numbers \(a\) and \(b\). By definition, \(a=\operatorname{Re}(z)\) and \(b=\operatorname{Im}(z)\), so the point associated with \(z\) is \((a, b)=(\operatorname{Re}(z), \operatorname{Im}(z))\). From Section 11.4, we know that if \((r, \theta)\) is a polar representation for \((\operatorname{Re}(z), \operatorname{Im}(z))\), then \(\tan (\theta)=\frac{\operatorname{Im}(z)}{\operatorname{Re}(z)}\), provided \(\operatorname{Re}(z) \neq 0\). If \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)>0\), then \(z\) lies on the positive imaginary axis. Since we take r > 0, we have that \(\theta\) is coterminal with \(\frac{\pi}{2}\), and the result follows. If \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)<0\), then \(z\) lies on the negative imaginary axis, and a similar argument shows \(\theta\) is coterminal with \(-\frac{\pi}{2}\). The last property in the theorem was already discussed in the remarks following Definition 11.2.
Our next goal is to completely marry the Geometry and the Algebra of the complex numbers. To that end, consider the figure below.
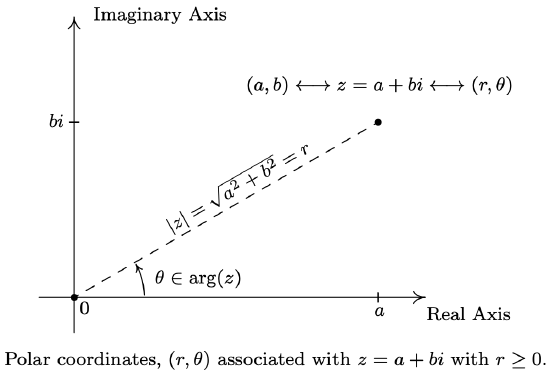
We know from Theorem 11.7 that \(a=r \cos (\theta)\) and \(b=r \sin (\theta)\). Making these substitutions for \(a\) and \(b\) gives \(z=a+b i=r \cos (\theta)+r \sin (\theta) i=r[\cos (\theta)+i \sin (\theta)]\). The expression '\(\cos (\theta)+i \sin (\theta)\)' is abbreviated \(\operatorname{cis}(\theta)\) so we can write \(z=r \operatorname{cis}(\theta)\). Since \(r=|z|\) and \(\theta \in \arg (z)\), we get
Suppose \(z\) is a complex number and \(\theta \in \arg (z)\). The expression:
\(|z| \operatorname{cis}(\theta)=|z|[\cos (\theta)+i \sin (\theta)]\)
is called a polar form for \(z\).
Since there are infinitely many choices for \(\theta \in \arg (z)\), there infinitely many polar forms for \(z\), so we used the indefinite article ‘a’ in Definition 11.3. It is time for an example.
- Find the rectangular form of the following complex numbers. Find \(\operatorname{Re}(z)\) and \(\operatorname{Im}(z)\).
- \(z=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\)
- \(z=2 \operatorname{cis}\left(-\frac{3 \pi}{4}\right)\)
- \(z=3 \operatorname{cis}(0)\)
- \(z=\operatorname{cis}\left(\frac{\pi}{2}\right)\)
- Use the results from Example 11.7.1 to find a polar form of the following complex numbers.
- \(z=\sqrt{3}-i\)
- \(z=-2+4 i\)
- \(z =i\)
- \(z = −117\)
Solution
- The key to this problem is to write out \(\operatorname{cis}(\theta)\) as \(\cos (\theta)+i \sin (\theta)\).
- By definitition, \(z=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)=4\left[\cos \left(\frac{2 \pi}{3}\right)+i \sin \left(\frac{2 \pi}{3}\right)\right]\). After some simplifying, we get \(z=-2+2 i \sqrt{3}\), so that \(\operatorname{Re}(z)=-2\) and \(\operatorname{Im}(z)=2 \sqrt{3}\).
- Expanding, we get \(z=2 \operatorname{cis}\left(-\frac{3 \pi}{4}\right)=2\left[\cos \left(-\frac{3 \pi}{4}\right)+i \sin \left(-\frac{3 \pi}{4}\right)\right]\). From this, we find \(z=-\sqrt{2}-i \sqrt{2}\), so \(\operatorname{Re}(z)=-\sqrt{2}=\operatorname{Im}(z)\).
- We get \(z=3 \operatorname{cis}(0)=3[\cos (0)+i \sin (0)]=3\). Writing \(3 = 3 + 0i\), we get \(\operatorname{Re}(z)=3\) and \(\operatorname{Im}(z)=0\), which makes sense seeing as 3 is a real number.
- Lastly, we have \(z=\operatorname{cis}\left(\frac{\pi}{2}\right)=\cos \left(\frac{\pi}{2}\right)+i \sin \left(\frac{\pi}{2}\right)=i\). Since \(i = 0 + 1i\), we get \(\operatorname{Re}(z)=0\) and \(\operatorname{Im}(z)=1\). Since \(i\) is called the ‘imaginary unit,’ these answers make pect sense.
- To write a polar form of a complex number \(z\), we need two pieces of information: the modulus \(|z|\) and an argument (not necessarily the principal argument) of \(z\). We shamelessly mine our solution to Example 11.7.1 to find what we need.
- For \(z=\sqrt{3}-i,|z|=2\) and \(\theta=-\frac{\pi}{6}\), so \(z=2 \operatorname{cis}\left(-\frac{\pi}{6}\right)\). We can check our answer by converting it back to rectangular form to see that it simplifies to \(z=\sqrt{3}-i\).
- For \(z=-2+4 i,|z|=2 \sqrt{5}\) and \(\theta=\pi-\arctan (2)\). Hence, \(z=2 \sqrt{5} \operatorname{cis}(\pi-\arctan (2))\). It is a good exercise to actually show that this polar form reduces to \(z=-2+4 i\).
- For \(z=3 i,|z|=3\) and \(\theta=\frac{\pi}{2}\). In this case, \(z=3 \operatorname{cis}\left(\frac{\pi}{2}\right)\). This can be checked geometrically. Head out 3 units from 0 along the positive real axis. Rotating \(\frac{\pi}{2}\) radians counter-clockwise lands you exactly 3 units above 0 on the imaginary axis at \(z=3i\).
- Last but not least, for \(z=-117,|z|=117\) and \(\theta=\pi\). We get \(z=117 \operatorname{cis}(\pi)\). As with the previous problem, our answer is easily checked geometrically.
The following theorem summarizes the advantages of working with complex numbers in polar form.
Suppose \(z\) and \(w\) are complex numbers with polar forms \(z=|z| \operatorname{cis}(\alpha)\) and \(w=|w| \operatorname{cis}(\beta)\). Then
- Product Rule: \(z w=|z||w| \operatorname{cis}(\alpha+\beta)\)
- Power Rule (DeMoivre’s Theorem): \(z^{n}=|z|^{n} \operatorname{cis}(n \theta)\) for every natural number \(n\)
- Quotient Rule: \(\frac{z}{w}=\frac{|z|}{|w|} \operatorname{cis}(\alpha-\beta)\), provided \(|w| \neq 0\)
The proof of Theorem 11.16 requires a healthy mix of definition, arithmetic and identities. We first start with the product rule.
\[\begin{aligned}
z w &=[|z| \operatorname{cis}(\alpha)][|w| \operatorname{cis}(\beta)] \\
&=|z||w|[\cos (\alpha)+i \sin (\alpha)][\cos (\beta)+i \sin (\beta)]
\end{aligned}\nonumber\]
We now focus on the quantity in brackets on the right hand side of the equation.
\[\begin{aligned}
{[\cos (\alpha)+i \sin (\alpha)][\cos (\beta)+i \sin (\beta)]=} & \cos (\alpha) \cos (\beta)+i \cos (\alpha) \sin (\beta) & \\
&+i \sin (\alpha) \cos (\beta)+i^{2} \sin (\alpha) \sin (\beta) & \\
=& \cos (\alpha) \cos (\beta)+i^{2} \sin (\alpha) \sin (\beta) & & \text { Rearranging terms } \\
&+i \sin (\alpha) \cos (\beta)+i \cos (\alpha) \sin (\beta) & \\
=&(\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta)) & & \text { Since } i^{2}=-1 \\
&+i(\sin (\alpha) \cos (\beta)+\cos (\alpha) \sin (\beta)) & & \text { Factor out } i \\
=& \cos (\alpha+\beta)+i \sin (\alpha+\beta) & & \text { Sum identities } \\
=& \operatorname{cis}(\alpha+\beta) && \text { Definition of 'cis' }
\end{aligned}\nonumber\]
Putting this together with our earlier work, we get \(z w=|z||w| \operatorname{cis}(\alpha+\beta)\), as required.
Moving right along, we next take aim at the Power Rule, better known as DeMoivre’s Theorem.9 We proceed by induction on \(n\). Let \(P(n)\) be the sentence \(z^{n}=|z|^{n} \operatorname{cis}(n \theta)\). Then \(P(1)\) is true, since \(z^{1}=z=|z| \operatorname{cis}(\theta)=|z|^{1} \operatorname{cis}(1 \cdot \theta)\). We now assume \(P(k)\) is true, that is, we assume \(z^{k}=|z|^{k} \operatorname{cis}(k \theta)\) for some \(k \geq 1\). Our goal is to show that \(P(k + 1)\) is true, or that \(z^{k+1}=|z|^{k+1} \operatorname{cis}((k+1) \theta)\). We have
\[\begin{aligned}
z^{k+1} &=z^{k} z & & \text { Properties of Exponents } \\
&=\left(|z|^{k} \operatorname{cis}(k \theta)\right)(|z| \operatorname{cis}(\theta)) & & \text { Induction Hypothesis } \\
&=\left(|z|^{k}|z|\right) \operatorname{cis}(k \theta+\theta) & & \text { Product Rule } \\
&=|z|^{k+1} \operatorname{cis}((k+1) \theta) & &
\end{aligned}\nonumber\]
Hence, assuming \(P(k)\) is true, we have that \(P(k + 1)\) is true, so by the Principle of Mathematical Induction, \(z^{n}=|z|^{n} \operatorname{cis}(n \theta)\) for all natural numbers \(n\).
The last property in Theorem 11.16 to prove is the quotient rule. Assuming \(|w| \neq 0\) we have
\[\begin{aligned}
\frac{z}{w} &=\frac{|z| \operatorname{cis}(\alpha)}{|w| \operatorname{cis}(\beta)} \\
&=\left(\frac{|z|}{|w|}\right) \frac{\cos (\alpha)+i \sin (\alpha)}{\cos (\beta)+i \sin (\beta)}
\end{aligned}\nonumber\]
Next, we multiply both the numerator and denominator of the right hand side by \((\cos (\beta)-i \sin (\beta))\) which is the complex conjugate of \((\cos (\beta)+i \sin (\beta))\) to get
\[\frac{z}{w}=\left(\frac{|z|}{|w|}\right) \frac{\cos (\alpha)+i \sin (\alpha)}{\cos (\beta)+i \sin (\beta)} \cdot \frac{\cos (\beta)-i \sin (\beta)}{\cos (\beta)-i \sin (\beta)}\nonumber\]
If we let the numerator be \(N=[\cos (\alpha)+i \sin (\alpha)][\cos (\beta)-i \sin (\beta)]\) and simplify we get
\[\begin{aligned}
N &=[\cos (\alpha)+i \sin (\alpha)][\cos (\beta)-i \sin (\beta)] & & \\
&=\cos (\alpha) \cos (\beta)-i \cos (\alpha) \sin (\beta)+i \sin (\alpha) \cos (\beta)-i^{2} \sin (\alpha) \sin (\beta) & & \text { Expand } \\
&=[\cos (\alpha) \cos (\beta)+\sin (\alpha) \sin (\beta)]+i[\sin (\alpha) \cos (\beta)-\cos (\alpha) \sin (\beta)] & & \text { Rearrange and Factor } \\
&=\cos (\alpha-\beta)+i \sin (\alpha-\beta) & & \text { Difference Identities } \\
&=\operatorname{cis}(\alpha-\beta) & & \text { Definition of 'cis' }
\end{aligned}\nonumber\]
If we call the denominator \(D\) then we get
\[\begin{aligned}
D &=[\cos (\beta)+i \sin (\beta)][\cos (\beta)-i \sin (\beta)] & \\
&=\cos ^{2}(\beta)-i \cos (\beta) \sin (\beta)+i \cos (\beta) \sin (\beta)-i^{2} \sin ^{2}(\beta) & & \text { Expand } \\
&=\cos ^{2}(\beta)-i^{2} \sin ^{2}(\beta) & & \text { Simplify } \\
&=\cos ^{2}(\beta)+\sin ^{2}(\beta) & & \text { Again, } i^{2}=-1 \\
&=1 & & \text { Pythagorean Identity }
\end{aligned}\nonumber\]
Putting it all together, we get
\[\begin{aligned}
\frac{z}{w} &=\left(\frac{|z|}{|w|}\right) \frac{\cos (\alpha)+i \sin (\alpha)}{\cos (\beta)+i \sin (\beta)} \cdot \frac{\cos (\beta)-i \sin (\beta)}{\cos (\beta)-i \sin (\beta)} \\
&=\left(\frac{|z|}{|w|}\right) \frac{\operatorname{cis}(\alpha-\beta)}{1} \\
&=\frac{|z|}{|w|} \operatorname{cis}(\alpha-\beta)
\end{aligned}\nonumber\]
and we are done. The next example makes good use of Theorem 11.16.
Let \(z=2 \sqrt{3}+2 i\) and \(w=-1+i \sqrt{3}\). Use Theorem 11.16 to find the following.
- \(zw\)
- \(w^{5}\)
- \(\frac{z}{w}\)
Write your final answers in rectangular form.
Solution
In order to use Theorem 11.16, we need to write z and w in polar form. For \(z=2 \sqrt{3}+2 i\), we find \(|z|=\sqrt{(2 \sqrt{3})^{2}+(2)^{2}}=\sqrt{16}=4\). If \(\theta \in \arg (z)\), we know \(\tan (\theta)=\frac{\operatorname{Im}(z)}{\operatorname{Re}(z)}=\frac{2}{2 \sqrt{3}}=\frac{\sqrt{3}}{3}\). Since \(z\) lies in Quadrant I, we have \(\theta=\frac{\pi}{6}+2 \pi k\) for integers \(k\). Hence, \(z=4 \operatorname{cis}\left(\frac{\pi}{6}\right)\). For \(w=-1+i \sqrt{3}\), we have \(|w|=\sqrt{(-1)^{2}+(\sqrt{3})^{2}}=2\). For an argument \(\theta\) of \(w\), we have \(\tan (\theta)=\frac{\sqrt{3}}{-1}=-\sqrt{3}\). Since \(w\) lies in Quadrant II, \(\theta=\frac{2 \pi}{3}+2 \pi k\) for integers \(k\) and \(w=2 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\). We can now proceed.
- We get \(z w=\left(4 \operatorname{cis}\left(\frac{\pi}{6}\right)\right)\left(2 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\right)=8 \operatorname{cis}\left(\frac{\pi}{6}+\frac{2 \pi}{3}\right)=8 \operatorname{cis}\left(\frac{5 \pi}{6}\right)=8\left[\cos \left(\frac{5 \pi}{6}\right)+i \sin \left(\frac{5 \pi}{6}\right)\right]\).
- We use DeMoivre’s Theorem which yeilds \(w^{5}=\left[2 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\right]^{5}=2^{5} \operatorname{cis}\left(5 \cdot \frac{2 \pi}{3}\right)=32 \operatorname{cis}\left(\frac{10 \pi}{3}\right)\). Since \(\frac{10 \pi}{3}\) is coterminal with \(\frac{4 \pi}{3}\), we get \(w^{5}=32\left[\cos \left(\frac{4 \pi}{3}\right)+i \sin \left(\frac{4 \pi}{3}\right)\right]=-16-16 i \sqrt{3}\).
- Last, but not least, we have \(\frac{z}{w}=\frac{4 \operatorname{cis}\left(\frac{\pi}{6}\right)}{2 \operatorname{cis}\left(\frac{2 \pi}{3}\right)}=\frac{4}{2} \operatorname{cis}\left(\frac{\pi}{6}-\frac{2 \pi}{3}\right)=2 \operatorname{cis}\left(-\frac{\pi}{2}\right)\). Since \(-\frac{\pi}{2}\) is a quadrantal angle, we can ‘see’ the rectangular form by moving out 2 units along the positive real axis, then rotating \(\frac{\pi}{2}\) radians clockwise to arrive at the point 2 units below 0 on the imaginary axis. The long and short of it is that \(\frac{z}{w}=-2 i\).
Some remarks are in order. First, the reader may not be sold on using the polar form of complex numbers to multiply complex numbers – especially if they aren’t given in polar form to begin with. Indeed, a lot of work was needed to convert the numbers \(z\) and \(w\) in Example 11.7.3 into polar form, compute their product, and convert back to rectangular form – certainly more work than is required \(z w=(2 \sqrt{3}+2 i)(-1+i \sqrt{3})\) the old-fashioned way. However, Theorem 11.16 pays huge dividends when computing powers of complex numbers. Consider how we computed \(w^{5}\) above and compare that to using the Binomial Theorem, Theorem 9.4, to accomplish the same feat by expanding \((-1+i \sqrt{3})^{5}\). Division is tricky in the best of times, and we saved ourselves a lot of time and effort using Theorem 11.16 to find and simplify \(\frac{z}{w}\) using their polar forms as opposed to starting with \(\frac{2 \sqrt{3}+2 i}{-1+i \sqrt{3}}\), rationalizing the denominator, and so forth.
There is geometric reason for studying these polar forms and we would be derelict in our duties if we did not mention the Geometry hidden in Theorem 11.16. Take the product rule, If \(z=|z| \operatorname{cis}(\alpha)\) and \(w=|w| \operatorname{cis}(\beta)\), the formula \(z w=|z||w| \operatorname{cis}(\alpha+\beta)\) can be viewed geometrically as a two step process. The multiplication \(|z|\) by \(|w|\) can be interpreted as magnifying10 the distance \(|z|\) from \(z\) to 0, by the factor \(|w|\). Adding the argument of \(w\) to the argument of \(z\) can be interpreted geometrically as a rotation of \(\beta\) radians counter-clockwise.11 Focusing on \(z\) and \(w\) from Example 11.7.3, we can arrive at the product \(zw\) by plotting \(z\), doubling its distance from 0 (since \(|w| = 2\)), and rotating \(\frac{2 \pi}{3}\) radians counter-clockwise. The sequence of diagrams below attempts to describe this process geometrically.
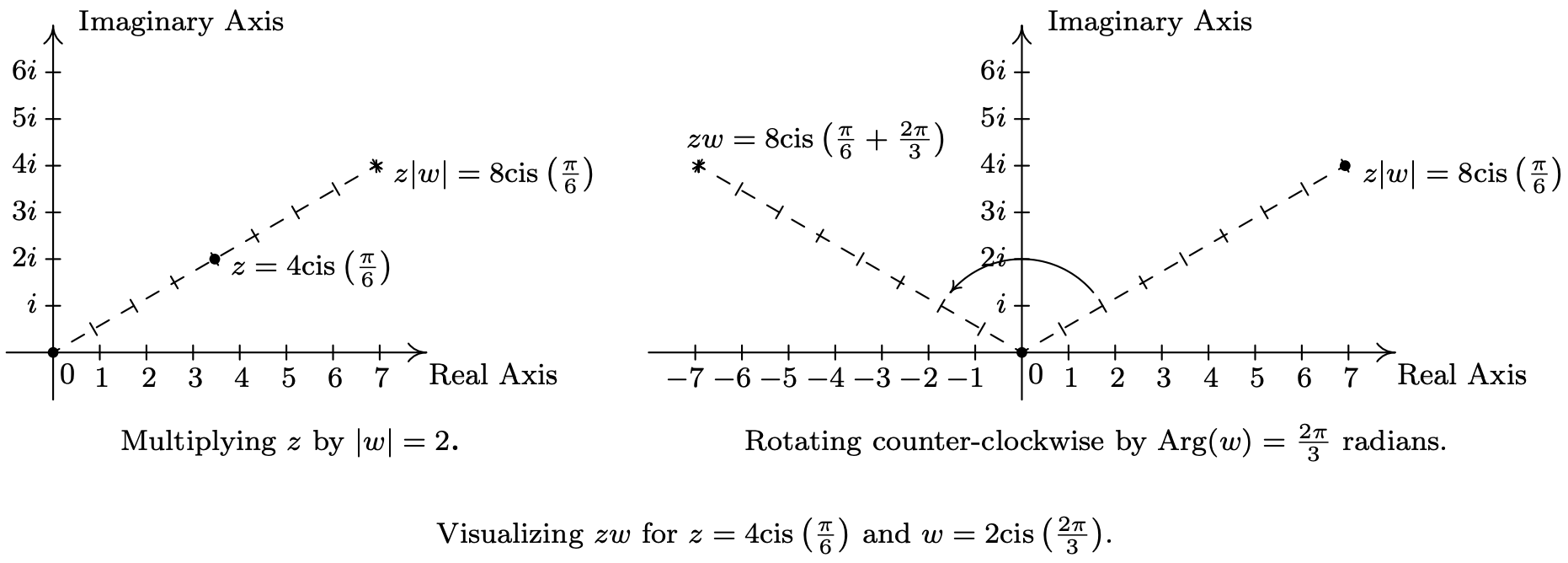
We may also visualize division similarly. Here, the formula \(\frac{z}{w}=\frac{|z|}{|w|} \operatorname{cis}(\alpha-\beta)\) may be interpreted as shrinking12 the distance from 0 to \(z\) by the factor \(|w|\), followed up by a clockwise13 rotation of \(\beta\) radians. In the case of \(z\) and \(w\) from Example 11.7.3, we arrive at \(\frac{z}{w}\) by first halving the distance from 0 to \(z\), then rotating clockwise \(\frac{2 \pi}{3}\) radians.
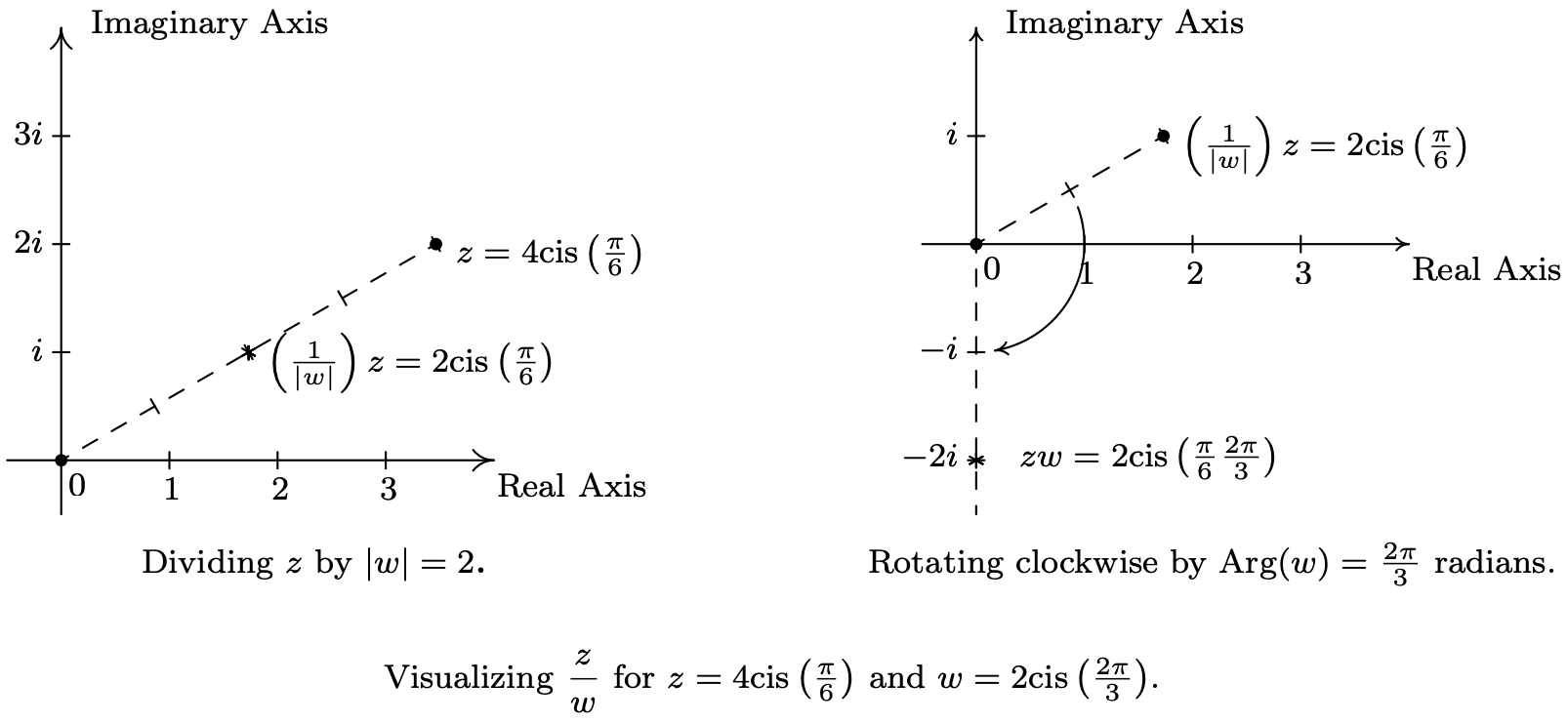
Our last goal of the section is to reverse DeMoivre’s Theorem to extract roots of complex numbers.
Let \(z\) and \(w\) be complex numbers. If there is a natural number \(n\) such that \(w^{n}=z\), then \(w\) is an \(n^{\text {th }}\) root of \(z\).
Unlike Definition 5.4 in Section 5.3, we do not specify one particular prinicpal \(n^{\text {th }}\) root, hence the use of the indefinite article 'an' as in 'an \(n^{\text {th }}\) root of \(z\)'. Using this definition, both 4 and - 4 are square roots of 16, while \(\sqrt{16}\) means the principal square root of 16 as in \(\sqrt{16}=4\). Suppose we wish to find all complex third (cube) roots of 8. Algebraically, we are trying to solve \(w^{3}=8\). We know that there is only one real solution to this equation, namely \(w=\sqrt[3]{8}=2\), but if we take the time to rewrite this equation as \(w^{3}-8=0\) and factor, we get \((w-2)\left(w^{2}+2 w+4\right)=0\). The quadratic factor gives two more cube root \(w=-1 \pm i \sqrt{3}\), for a total of three cube roots of 8. In accordance with Theorem 3.14, since the degree of \(p(w)=w^{3}-8\) is three, there are three complex zeros, counting multiplicity. Since we have found three distinct zeros, we know these are all of the zeros, so there are exactly three distinct cube roots of 8. Let us now solve this same problem using the machinery developed in this section. To do so, we express \(z = 8\) in polar form. Since \(z = 8\) lies 8 units away on the positive real axis, we get \(z=8 \operatorname{cis}(0)\). If we let \(w=|w| \operatorname{cis}(\alpha)\) be a polar form of \(w\), the equation \(w^{3}=8\) becomes
\[\begin{aligned}
w^{3} &=8 \\
(|w| \operatorname{cis}(\alpha))^{3} &=8 \operatorname{cis}(0) \\
|w|^{3} \operatorname{cis}(3 \alpha) &=8 \operatorname{cis}(0) \quad \text { DeMoivre's Theorem }
\end{aligned}\nonumber\]
The complex number on the left hand side of the equation corresponds to the point with polar coordinate \(\left(|w|^{3}, 3 \alpha\right)\), while the complex number on the right hand side corresponds to the point with polar coordinates (8, 0). Since \(|w| \geq 0\), so is \(|w|^{3}\), which means \(\left(|w|^{3}, 3 \alpha\right)\) and (8, 0) are two polar representations corresponding to the same complex number, both with positive \(r\) values. From Section 11.4, we know \(|w|^{3}=8\) and \(3 \alpha=0+2 \pi k\) for integers \(k\). Since \(|w|\) is a real number, we solve \(|w|^{3}=8\) by extracting the principal cube root to get \(|w|=\sqrt[3]{8}=2\). As for \(\alpha\), we get \(\alpha=\frac{2 \pi k}{3}\) for integers \(k\). This produces three distinct points with polar coordinates corresponding to \(k = 0\), \(1\) and \(2\): specifically \((2, 0)\), \(\left(2, \frac{2 \pi}{3}\right)\) and \(\left(2, \frac{4 \pi}{3}\right)\). These correspond to the complex numbers \(w_{0}=2 \operatorname{cis}(0), w_{1}=2 \operatorname{cis}\left(\frac{2 \pi}{3}\right) \text { and } w_{2}=2 \operatorname{cis}\left(\frac{4 \pi}{3}\right)\), respectively. Writing these out in rectangular form yields \(w_{0}=2, w_{1}=-1+i \sqrt{3} \text { and } w_{2}=-1-i \sqrt{3}\). While this process seems a tad more involved than our previous factoring approach, this procedure can be generalized to find, for example, all of the fifth roots of 32. (Try using Chapter 3 techniques on that!) If we start with a generic complex number in polar form \(z=|z| \operatorname{cis}(\theta)\) and solve \(w^{n}=z\) in the same manner as above, we arrive at the following theorem.
Let \(z \neq 0\) be a complex number with polar form \(z=r \operatorname{cis}(\theta)\). For each natural number \(n\), \(z\) has \(n\) distinct \(n^{\text {th }}\) roots, which we denote by \(w_{0}, w_{1}, \ldots, w_{n-1}\), and they are given by the formula
\[w_{k}=\sqrt[n]{r} \operatorname{cis}\left(\frac{\theta}{n}+\frac{2 \pi}{n} k\right)\nonumber\]
The proof of Theorem 11.17 breaks into to two parts: first, showing that each \(w_{k}\) is an \(n^{\text {th }}\) root, and second, showing that the set \(\left\{w_{k} \mid k=0,1, \ldots,(n-1)\right\}\) consists of \(n\) different complex numbers. To show \(w_{k}\) is an \(n^{\text {th }}\) root of \(z\), we use DeMoivre’s Theorem to show \(\left(w_{k}\right)^{n}=z\).
\[\begin{aligned}
\left(w_{k}\right)^{n} &=\left(\sqrt[n]{r} \operatorname{cis}\left(\frac{\theta}{n}+\frac{2 \pi}{n} k\right)\right)^{n} \\
&=(\sqrt[n]{r})^{n} \operatorname{cis}\left(n \cdot\left[\frac{\theta}{n}+\frac{2 \pi}{n} k\right]\right) \quad \text { DeMoivre's Theorem } \\
&=r \operatorname{cis}(\theta+2 \pi k)
\end{aligned}\nonumber\]
Since \(k\) is a whole number, \(\cos (\theta+2 \pi k)=\cos (\theta)\) and \(\sin (\theta+2 \pi k)=\sin (\theta)\). Hence, it follows that \(\operatorname{cis}(\theta+2 \pi k)=\operatorname{cis}(\theta)\), so \(\left(w_{k}\right)^{n}=r \operatorname{cis}(\theta)=z\), as required. To show that the formula in Theorem 11.17 generates \(n\) distinct numbers, we assume \(n \geq 2\) (or else there is nothing to prove) and note that the modulus of each of the \(w_{k}\) is the same, namely \(\sqrt[n]{r}\). Therefore, the only way any two of these polar forms correspond to the same number is if their arguments are coterminal – that is, if the arguments differ by an integer multiple of \(2 \pi\). Suppose \(k\) and \(j\) are whole numbers between 0 and \((n−1)\), inclusive, with \(k \neq j\). Since \(k\) and \(j\) are different, let’s assume for the sake of argument that \(k > j\). Then \(\left(\frac{\theta}{n}+\frac{2 \pi}{n} k\right)-\left(\frac{\theta}{n}+\frac{2 \pi}{n} j\right)=2 \pi\left(\frac{k-j}{n}\right)\). For this to be an integer multiple of \(2 \pi\), \((k − j)\) must be a multiple of \(n\). But because of the restrictions on \(k\) and \(j\), \(0 < k − j ≤ n − 1\). (Think this through.) Hence, \((k − j)\) is a positive number less than \(n\), so it cannot be a multiple of n. As a result, \(w_{k}\) and \(w_{j}\) are different complex numbers, and we are done. By Theorem 3.14, we know there at most \(n\) distinct solutions to \(w^{n}=z\), and we have just found all of them. We illustrate Theorem 11.17 in the next example.
Use Theorem 11.17 to find the following:
- both square roots of \(z=-2+2 i \sqrt{3}\)
- the four fourth roots \(z=-16\)
- the three cube roots of \(z=\sqrt{2}+i \sqrt{2}\)
- the five fifth roots of \(z=1\).
Solution
- We start by writing \(z=-2+2 i \sqrt{3}=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\). To use Theorem 11.17, we identify \(r=4\), \(\theta=\frac{2 \pi}{3}\) and \(n=3\). We know that \(z\) has two square roots, and in keeping with the notation in Theorem 11.17, we’ll call them \(w_{0}\) and \(w_{1}\). We get \(w_{0}=\sqrt{4} \operatorname{cis}\left(\frac{(2 \pi / 3)}{2}+\frac{2 \pi}{2}(0)\right)=2 \operatorname{cis}\left(\frac{\pi}{3}\right)\) and \(w_{1}=\sqrt{4} \operatorname{cis}\left(\frac{(2 \pi / 3)}{2}+\frac{2 \pi}{2}(1)\right)=2 \operatorname{cis}\left(\frac{4 \pi}{3}\right)\). In rectangular form, the two square roots of \(z\) are \(w_{0}=1+i \sqrt{3}\) and \(w_{1}=-1-i \sqrt{3}\). We can check our answers by squaring them and showing that we get \(z=-2+2 i \sqrt{3}\).
- Proceeding as above, we get \(z=-16=16 \operatorname{cis}(\pi)\). With \(r=16\), \(\theta=\pi\) and \(n = 4\), we get the four fourth roots of \(z\) to be \(w_{0}=\sqrt[4]{16} \operatorname{cis}\left(\frac{\pi}{4}+\frac{2 \pi}{4}(0)\right)=2 \operatorname{cis}\left(\frac{\pi}{4}\right)\), \(w_{1}=\sqrt[4]{16} \operatorname{cis}\left(\frac{\pi}{4}+\frac{2 \pi}{4}(1)\right)=2 \operatorname{cis}\left(\frac{3\pi}{4} \right)\), \(w_{2}=\sqrt[4]{16} \operatorname{cis}\left(\frac{\pi}{4}+\frac{2 \pi}{4}(2)\right)=2 \operatorname{cis}\left(\frac{5 \pi}{4}\right)\) and \(w_{3}=\sqrt[4]{16} \operatorname{cis}\left(\frac{\pi}{4}+\frac{2 \pi}{4}(3)\right)=2 \operatorname{cis}\left(\frac{7 \pi}{4}\right)\). Converting these to rectangular form gives \(w_{0}=\sqrt{2}+i \sqrt{2}, w_{1}=-\sqrt{2}+i \sqrt{2}, w_{2}=-\sqrt{2}-i \sqrt{2}\) and \(w_{3}=\sqrt{2}-i \sqrt{2}\).
- For \(z=\sqrt{2}+i \sqrt{2}\), we have \(z=2 \operatorname{cis}\left(\frac{\pi}{4}\right)\). With \(r=2\), \(\theta=\frac{\pi}{4}\) and \(n = 3\) the usual computations yield \(w_{0}=\sqrt[3]{2} \operatorname{cis}\left(\frac{\pi}{12}\right), w_{1}=\sqrt[3]{2} \operatorname{cis}\left(\frac{9 \pi}{12}\right)=\sqrt[3]{2} \operatorname{cis}\left(\frac{3 \pi}{4}\right)\) and \(w_{2}=\sqrt[3]{2} \operatorname{cis}\left(\frac{17 \pi}{12}\right)\). If we were to convert these to rectangular form, we would need to use either the Sum and Difference Identities in Theorem 10.16 or the Half-Angle Identities in Theorem 10.19 to evaluate \(w_{0}\) and \(w_{2}\). Since we are not explicitly told to do so, we leave this as a good, but messy, exercise.
- To find the five fifth roots of 1, we write \(1=1 \operatorname{cis}(0)\). We have \(r=1, \theta=0 \text { and } n=5\). Since \(\sqrt[5]{1}=1\), the roots are \(w_{0}=\operatorname{cis}(0)=1, w_{1}=\operatorname{cis}\left(\frac{2 \pi}{5}\right), w_{2}=\operatorname{cis}\left(\frac{4 \pi}{5}\right), w_{3}=\operatorname{cis}\left(\frac{6 \pi}{5}\right)\) and \(w_{4}=\operatorname{cis}\left(\frac{8 \pi}{5}\right)\). The situation here is even graver than in the previous example, since we have not developed any identities to help us determine the cosine or sine of \(\frac{2 \pi}{5}\). At this stage, we could approximate our answers using a calculator, and we leave this as an exercise.
Now that we have done some computations using Theorem 11.17, we take a step back to look at things geometrically. Essentially, Theorem 11.17 says that to find the \(n^{\text {th }}\) roots of a complex number, we first take the \(n^{\text {th }}\) root of the modulus and divide the argument by \(n\). This gives the first root \(w_{0}\). Each succeessive root is found by adding \(\frac{2 \pi}{n}\) to the argument, which amounts to rotating \(w_{0}\) by \(\frac{2 \pi}{n}\) radians. This results in \(n\) roots, spaced equally around the complex plane. As an example of this, we plot our answers to number 2 in Example 11.7.4 below.
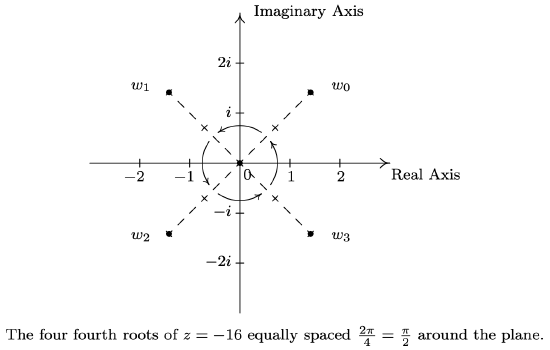
We have only glimpsed at the beauty of the complex numbers in this section. The complex plane is without a doubt one of the most important mathematical constructs ever devised. Coupled with Calculus, it is the venue for incredibly important Science and Engineering applications.14 For now, the following exercises will have to suffice.
11.7.1 Exercises
In Exercises 1 - 20, find a polar representation for the complex number \(z\) and then identify \(\operatorname{Re}(z)\), \(\operatorname{Im}(z),|z|, \arg (z)\) and \(\operatorname{Arg}(z)\).
- \(z=9+9 i\)
- \(z=5+5 i \sqrt{3}\)
- \(z = 6i\)
- \(z=-3 \sqrt{2}+3 i \sqrt{2}\)
- \(z=-6 \sqrt{3}+6 i\)
- \(z = −2\)
- \(z=-\frac{\sqrt{3}}{2}-\frac{1}{2} i\)
- \(z = −3 − 3i\)
- \(z = −5i\)
- \(z=2 \sqrt{2}-2 i \sqrt{2}\)
- \(z = 6\)
- \(z=i \sqrt[3]{7}\)
- \(z = 3 + 4i\)
- \(z=\sqrt{2}+i\)
- \(z = −7 + 24i\)
- \(z = −2 + 6i\)
- \(z = −12 − 5i\)
- \(z = −5 − 2i\)
- \(z = 4 − 2i\)
- \(z = 1 − 3i\)
In Exercises 21 - 40, find the rectangular form of the given complex number. Use whatever identities are necessary to find the exact values.
- \(z=6 \operatorname{cis}(0)\)
- \(z=2 \operatorname{cis}\left(\frac{\pi}{6}\right)\)
- \(z=7 \sqrt{2} \operatorname{cis}\left(\frac{\pi}{4}\right)\)
- \(z=3 \operatorname{cis}\left(\frac{\pi}{2}\right)\)
- \(z=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)\)
- \(z=\sqrt{6} \operatorname{cis}\left(\frac{3 \pi}{4}\right)\)
- \(z=9 \operatorname{cis}(\pi)\)
- \(z=3 \operatorname{cis}\left(\frac{4 \pi}{3}\right)\)
- \(z=7 \operatorname{cis}\left(-\frac{3 \pi}{4}\right)\)
- \(z=\sqrt{13} \operatorname{cis}\left(\frac{3 \pi}{2}\right)\)
- \(z=\frac{1}{2} \operatorname{cis}\left(\frac{7 \pi}{4}\right)\)
- \(z=12 \operatorname{cis}\left(-\frac{\pi}{3}\right)\)
- \(z=8 \operatorname{cis}\left(\frac{\pi}{12}\right)\)
- \(z=2 \operatorname{cis}\left(\frac{7 \pi}{8}\right)\)
- \(z=5 \operatorname{cis}\left(\arctan \left(\frac{4}{3}\right)\right)\)
- \(z=\sqrt{10} \operatorname{cis}\left(\arctan \left(\frac{1}{3}\right)\right)\)
- \(z=15 \operatorname{cis}(\arctan (-2))\)
- \(z=\sqrt{3}(\arctan (-\sqrt{2}))\)
- \(z=50 \operatorname{cis}\left(\pi-\arctan \left(\frac{7}{24}\right)\right)\)
- \(z=\frac{1}{2} \operatorname{cis}\left(\pi+\arctan \left(\frac{5}{12}\right)\right)\)
For Exercises 41 - 52, use \(z=-\frac{3 \sqrt{3}}{2}+\frac{3}{2} i\) and \(w=3 \sqrt{2}-3 i \sqrt{2}\) to compute the quantity. Express your answers in polar form using the principal argument.
- \(zw\)
- \(\frac{z}{w}\)
- \(\frac{w}{z}\)
- \(z^{4}\)
- \(w^{3}\)
- \(z^{5} w^{2}\)
- \(z^{3} w^{2}\)
- \(\frac{z^{2}}{w}\)
- \(\frac{w}{z^{2}}\)
- \(\frac{z^{3}}{w^{2}}\)
- \(\frac{w^{2}}{z^{3}}\)
- \(\left(\frac{w}{z}\right)^{6}\)
In Exercises 53 - 64, use DeMoivre’s Theorem to find the indicated power of the given complex number. Express your final answers in rectangular form.
- \((-2+2 i \sqrt{3})^{3}\)
- \((-\sqrt{3}-i)^{3}\)
- \((-3+3 i)^{4}\)
- \((\sqrt{3}+i)^{4}\)
- \(\left(\frac{5}{2}+\frac{5}{2} i\right)^{3}\)
- \(\left(-\frac{1}{2}-\frac{\sqrt{3}}{2} i\right)^{6}\)
- \(\left(\frac{3}{2}-\frac{3}{2} i\right)^{3}\)
- \(\left(\frac{\sqrt{3}}{3}-\frac{1}{3} i\right)^{4}\)
- \(\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i\right)^{4}\)
- \((2+2 i)^{5}\)
- \((\sqrt{3}-i)^{5}\)
- \((1-i)^{8}\)
In Exercises 65 - 76, find the indicated complex roots. Express your answers in polar form and then convert them into rectangular form.
- the two square roots of \(z = 4i\)
- the two square roots of \(z = −25i\)
- the two square roots of \(z=1+i \sqrt{3}\)
- the two square roots of \(\frac{5}{2}-\frac{5 \sqrt{3}}{2} i\)
- the three cube roots of \(z = 64\)
- the three cube roots of \(z = −125\)
- the three cube roots of \(z = i\)
- the three cube roots of \(z = −8i\)
- the four fourth roots of \(z = 16\)
- the four fourth roots of \(z = −81\)
- the six sixth roots of \(z = 64\)
- the six sixth roots of \(z = −729\)
- Use the Sum and Difference Identities in Theorem 10.16 or the Half Angle Identities in Theorem 10.19 to express the three cube roots of \(z=\sqrt{2}+i \sqrt{2}\) in rectangular form. (See Example 11.7.4, number 3.)
- Use a calculator to approximate the five fifth roots of 1. (See Example 11.7.4, number 4.)
- According to Theorem 3.16 in Section 3.4, the polynomial \(p(x)=x^{4}+4\) can be factored into the product linear and irreducible quadratic factors. In Exercise 28 in Section 8.7, we showed you how to factor this polynomial into the product of two irreducible quadratic factors using a system of non-linear equations. Now that we can compute the complex fourth roots of −4 directly, we can simply apply the Complex Factorization Theorem, Theorem 3.14, to obtain the linear factorization \(p(x) = (x − (1 + i))(x − (1 − i))(x − (−1 + i))(x − (−1 − i))\). By multiplying the first two factors together and then the second two factors together, thus pairing up the complex conjugate pairs of zeros Theorem 3.15 told us we’d get, we have that \(p(x)=\left(x^{2}-2 x+2\right)\left(x^{2}+2 x+2\right)\). Use the 12 complex 12th roots of 4096 to factor \(p(x)=x^{12}-4096\) into a product of linear and irreducible quadratic factors.
- Complete the proof of Theorem 11.14 by showing that if \(w \neq 0\) than \(\left|\frac{1}{w}\right|=\frac{1}{|w|}\).
- Recall from Section 3.4 that given a complex number \(z = a+bi\) its complex conjugate, denoted \(\bar{z}\), is given by \(\bar{z}=a-b i\).
- Prove that \(|\bar{z}|=|z|\).
- Prove that \(|z|=\sqrt{z \bar{z}}\)
- Show that \(\operatorname{Re}(z)=\frac{z+\bar{z}}{2}\) and \(\operatorname{Im}(z)=\frac{z-\bar{z}}{2 i}\)
- Show that if \(\theta \in \arg (z)\) then \(-\theta \in \arg (\bar{z})\). Interpret this result geometrically.
- Is it always true that \(\operatorname{Arg}(\bar{z})=-\operatorname{Arg}(z)\)?
- Given any natural number \(n \geq 2\), the \(n\) complex \(n^{\text {th }}\) roots of the number \(z = 1\) are called the \(n^{\text {th }}\) Roots of Unity. In the following exercises, assume that \(n\) is a fixed, but arbitrary, natural number such that \(n \geq 2\).
- Show that \(w = 1\) is an \(n^{\text {th }}\) root of unity.
- Show that if both \(w_{j}\) and \(w_{k}\) are \(n^{\text {th }}\) roots of unity then so is their product \(w_{j} w_{k}\).
- Show that if \(w_{j}\) is an \(n^{\text {th }}\) root of unity then there exists another \(n^{\text {th }}\) root of unity \(w_{j^{\prime}}\) such that \(w_{j} w_{j^{\prime}}=1\). Hint: If \(w_{j}=\operatorname{cis}(\theta)\) let \(w_{j^{\prime}}=\operatorname{cis}(2 \pi-\theta)\). You’ll need to verify that \(w_{j^{\prime}}=\operatorname{cis}(2 \pi-\theta)\) is indeed an \(n^{\text {th }}\) root of unity.
- Another way to express the polar form of a complex number is to use the exponential function. For real numbers \(t\), Euler’s Formula defines \(e^{i t}=\cos (t)+i \sin (t)\).
- Use Theorem 11.16 to show that \(e^{i x} e^{i y}=e^{i(x+y)}\) for all real numbers \(x\) and \(y\).
- Use Theorem 11.16 to show that \(\left(e^{i x}\right)^{n}=e^{i(n x)}\) for any real number \(x\) and any natural number \(n\).
- Use Theorem 11.16 to show that \(\frac{e^{i x}}{e^{i y}}=e^{i(x-y)}\) for all real numbers \(x\) and \(y\).
- If \(z=r \operatorname{cis}(\theta)\) is the polar form of \(z\), show that \(z=r e^{i t}\) where \(\theta=t\) radians.
- Show that \(e^{i \pi}+1=0\). (This famous equation relates the five most important constants in all of Mathematics with the three most fundamental operations in Mathematics.)
- Show that \(\cos (t)=\frac{e^{i t}+e^{-i t}}{2}\) and that \(\sin (t)=\frac{e^{i t}-e^{-i t}}{2 i}\) for all real numbers \(t\).
11.7.2 Answers
- \(\begin{aligned}
&z=9+9 i=9 \sqrt{2} \operatorname{cis}\left(\frac{\pi}{4}\right), \quad \operatorname{Re}(z)=9, \quad \operatorname{Im}(z)=9, \quad|z|=9 \sqrt{2} \\
&\arg (z)=\left\{\frac{\pi}{4}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{\pi}{4}.
\end{aligned}\) - \(\begin{aligned}
&z=5+5 i \sqrt{3}=10 \operatorname{cis}\left(\frac{\pi}{3}\right), \quad \operatorname{Re}(z)=5, \quad \operatorname{Im}(z)=5 \sqrt{3}, \quad|z|=10 \\
&\arg (z)=\left\{\frac{\pi}{3}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{\pi}{3}
\end{aligned}\) - \(\begin{aligned}
&z=6 i=6 \operatorname{cis}\left(\frac{\pi}{2}\right), \quad \operatorname{Re}(z)=0, \quad \operatorname{Im}(z)=6, \quad|z|=6 \\
&\arg (z)=\left\{\frac{\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=-3 \sqrt{2}+3 i \sqrt{2}=6 \operatorname{cis}\left(\frac{3 \pi}{4}\right), \quad \operatorname{Re}(z)=-3 \sqrt{2}, \quad \operatorname{Im}(z)=3 \sqrt{2}, \quad|z|=6 \\
&\arg (z)=\left\{\frac{3\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{3\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=-6 \sqrt{3}+6 i=12 \operatorname{cis}\left(\frac{5 \pi}{6}\right), \quad \operatorname{Re}(z)=-6 \sqrt{3}, \quad \operatorname{Im}(z)=6, \quad|z|=12 \\
&\arg (z)=\left\{\frac{5\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{5\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=-2=2 \operatorname{cis}(\pi), \quad \operatorname{Re}(z)=-2, \quad \operatorname{Im}(z)=0, \quad|z|=2\\
&\arg (z)=\left\{(2k+1)\pi \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\pi.
\end{aligned}\) - \(\begin{aligned}
&z=-\frac{\sqrt{3}}{2}-\frac{1}{2} i=\operatorname{cis}\left(\frac{7 \pi}{6}\right), \quad \operatorname{Re}(z)=-\frac{\sqrt{3}}{2}, \quad \operatorname{Im}(z)=-\frac{1}{2}, \quad|z|=1 \\
&\arg (z)=\left\{\frac{7\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=-\frac{5\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=-3-3 i=3 \sqrt{2} \operatorname{cis}\left(\frac{5 \pi}{4}\right), \quad \operatorname{Re}(z)=-3, \quad \operatorname{Im}(z)=-3, \quad|z|=3 \sqrt{2} \\
&\arg (z)=\left\{\frac{5\pi}{4}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=-\frac{3\pi}{4}.
\end{aligned}\) - \(\begin{aligned}
&z=-5 i=5 \operatorname{cis}\left(\frac{3 \pi}{2}\right), \quad \operatorname{Re}(z)=0, \quad \operatorname{Im}(z)=-5, \quad|z|=5 \\
&\arg (z)=\left\{\frac{3\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=-\frac{\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=2 \sqrt{2}-2 i \sqrt{2}=4 \operatorname{cis}\left(\frac{7 \pi}{4}\right), \quad \operatorname{Re}(z)=2 \sqrt{2}, \quad \operatorname{Im}(z)=-2 \sqrt{2}, \quad|z|=4 \\
&\arg (z)=\left\{\frac{7\pi}{4}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=-\frac{\pi}{4}.
\end{aligned}\) - \(\begin{aligned}
&z=6=6 \operatorname{cis}(0), \quad \operatorname{Re}(z)=6, \quad \operatorname{Im}(z)=0, \quad|z|=6 \\
&\arg (z)=\left\{2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=0.
\end{aligned}\) - \(\begin{aligned}
&z=i \sqrt[3]{7}=\sqrt[3]{7} \operatorname{cis}\left(\frac{\pi}{2}\right), \quad \operatorname{Re}(z)=0, \quad \operatorname{Im}(z)=\sqrt[3]{7}, \quad|z|=\sqrt[3]{7}
\\ &\arg (z)=\left\{\frac{\pi}{2}+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\frac{\pi}{2}.
\end{aligned}\) - \(\begin{aligned}
&z=3+4 i=5 \operatorname{cis}\left(\arctan \left(\frac{4}{3}\right)\right), \quad \operatorname{Re}(z)=3, \quad \operatorname{Im}(z)=4, \quad|z|=5
\\ &\arg (z)=\left\{\operatorname{arctan}\left(\frac{4}{3}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}\left(\frac{4}{3}\right).
\end{aligned}\) - \(\begin{aligned}
&z=\sqrt{2}+i=\sqrt{3} \operatorname{cis}\left(\arctan \left(\frac{\sqrt{2}}{2}\right)\right), \quad \operatorname{Re}(z)=\sqrt{2}, \quad \operatorname{Im}(z)=1, \quad|z|=\sqrt{3}
\\ &\arg (z)=\left\{\operatorname{arctan}\left(\frac{\sqrt{2}}{2}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}\left(\frac{\sqrt{2}}{2}\right).
\end{aligned}\) - \(\begin{aligned}
&z=-7+24 i=25 \operatorname{cis}\left(\pi-\arctan \left(\frac{24}{7}\right)\right), \quad \operatorname{Re}(z)=-7, \quad \operatorname{Im}(z)=24, \quad|z|=25
\\ &\arg (z)=\left\{\pi-\operatorname{arctan}\left(\frac{24}{7}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\pi-\operatorname{arctan}\left(\frac{24}{7}\right).
\end{aligned}\) - \(\begin{aligned}
&z=-2+6 i=2 \sqrt{10} \operatorname{cis}(\pi-\arctan (3)), \quad \operatorname{Re}(z)=-2, \quad \operatorname{Im}(z)=6, \quad|z|=2 \sqrt{10}
\\ &\arg (z)=\left\{\pi-\operatorname{arctan}(3)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\pi-\operatorname{arctan}(3).
\end{aligned}\) - \(\begin{aligned}
&z=-12-5 i=13 \operatorname{cis}\left(\pi+\arctan \left(\frac{5}{12}\right)\right), \quad \operatorname{Re}(z)=-12, \quad \operatorname{Im}(z)=-5, \quad|z|=13
\\ &\arg (z)=\left\{\pi+\operatorname{arctan}\left(\frac{5}{12}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}\left(\frac{5}{12}\right)-\pi.
\end{aligned}\) - \(\begin{aligned}
&z=-5-2 i=\sqrt{29} \operatorname{cis}\left(\pi+\arctan \left(\frac{2}{5}\right)\right), \quad \operatorname{Re}(z)=-5, \quad \operatorname{Im}(z)=-2, \quad|z|=\sqrt{29}
\\ &\arg (z)=\left\{\pi+\operatorname{arctan}\left(\frac{2}{5}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}\left(\frac{2}{5}\right)-\pi.
\end{aligned}\) - \(\begin{aligned}
&z=4-2 i=2 \sqrt{5} \operatorname{cis}\left(\arctan \left(-\frac{1}{2}\right)\right), \quad \operatorname{Re}(z)=4, \quad \operatorname{Im}(z)=-2, \quad|z|=2 \sqrt{5}
\\ &\arg (z)=\left\{\operatorname{arctan}\left(-\frac{1}{2}\right)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}\left(-\frac{1}{2}\right)=-\operatorname{arctan}\left(\frac{1}{2}\right).
\end{aligned}\) - \(\begin{aligned}
&z=1-3 i=\sqrt{10} \operatorname{cis}(\arctan (-3)), \quad \operatorname{Re}(z)=1, \quad \operatorname{Im}(z)=-3, \quad|z|=\sqrt{10}
\\ &\arg (z)=\left\{\operatorname{arctan}(-3)+2 \pi k \mid k \text { is an integer }\right\} \text { and } \operatorname{Arg}(z)=\operatorname{arctan}(-3)=-\operatorname{arctan}(3).
\end{aligned}\) - \(z=6 \operatorname{cis}(0)=6\)
- \(z=2 \operatorname{cis}\left(\frac{\pi}{6}\right)=\sqrt{3}+i\)
- \(z=7 \sqrt{2} \operatorname{cis}\left(\frac{\pi}{4}\right)=7+7 i\)
- \(z=3 \operatorname{cis}\left(\frac{\pi}{2}\right)=3 i\)
- \(z=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)=-2+2 i \sqrt{3}\)
- \(z=\sqrt{6} \operatorname{cis}\left(\frac{3 \pi}{4}\right)=-\sqrt{3}+i \sqrt{3}\)
- \(z=9 \operatorname{cis}(\pi)=-9\)
- \(z=3 \operatorname{cis}\left(\frac{4 \pi}{3}\right)=-\frac{3}{2}-\frac{3 i \sqrt{3}}{2}\)
- \(z=7 \operatorname{cis}\left(-\frac{3 \pi}{4}\right)=-\frac{7 \sqrt{2}}{2}-\frac{7 \sqrt{2}}{2} i\)
- \(z=\sqrt{13} \operatorname{cis}\left(\frac{3 \pi}{2}\right)=-i \sqrt{13}\)
- \(z=\frac{1}{2} \operatorname{cis}\left(\frac{7 \pi}{4}\right)=\frac{\sqrt{2}}{4}-i \frac{\sqrt{2}}{4}\)
- \(z=12 \operatorname{cis}\left(-\frac{\pi}{3}\right)=6-6 i \sqrt{3}\)
- \(z=8 \operatorname{cis}\left(\frac{\pi}{12}\right)=4 \sqrt{2+\sqrt{3}}+4 i \sqrt{2-\sqrt{3}}\)
- \(z=2 \operatorname{cis}\left(\frac{7 \pi}{8}\right)=-\sqrt{2+\sqrt{2}}+i \sqrt{2-\sqrt{2}}\)
- \(z=5 \operatorname{cis}\left(\arctan \left(\frac{4}{3}\right)\right)=3+4 i\)
- \(z=\sqrt{10} \operatorname{cis}\left(\arctan \left(\frac{1}{3}\right)\right)=3+i\)
- \(z=15 \operatorname{cis}(\arctan (-2))=3 \sqrt{5}-6 i \sqrt{5}\)
- \(z=\sqrt{3} \operatorname{cis}(\arctan (-\sqrt{2}))=1-i \sqrt{2}\)
- \(z=50 \operatorname{cis}\left(\pi-\arctan \left(\frac{7}{24}\right)\right)=-48+14 i\)
- \(z=\frac{1}{2} \operatorname{cis}\left(\pi+\arctan \left(\frac{5}{12}\right)\right)=-\frac{6}{13}-\frac{5 i}{26}\)
In Exercises 41 - 52, we have that \(z=-\frac{3 \sqrt{3}}{2}+\frac{3}{2} i=3 \operatorname{cis}\left(\frac{5 \pi}{6}\right)\) and \(w=3 \sqrt{2}-3 i \sqrt{2}=6 \operatorname{cis}\left(-\frac{\pi}{4}\right)\) so we get the following.
- \(z w=18 \operatorname{cis}\left(\frac{7 \pi}{12}\right)\)
- \(\frac{z}{w}=\frac{1}{2} \operatorname{cis}\left(-\frac{11 \pi}{12}\right)\)
- \(\frac{w}{z}=2 \operatorname{cis}\left(\frac{11 \pi}{12}\right)\)
- \(z^{4}=81 \operatorname{cis}\left(-\frac{2 \pi}{3}\right)\)
- \(w^{3}=216 \operatorname{cis}\left(-\frac{3 \pi}{4}\right)\)
- \(z^{5} w^{2}=8748 \operatorname{cis}\left(-\frac{\pi}{3}\right)\)
- \(z^{3} w^{2}=972 \operatorname{cis}(0)\)
- \(\frac{z^{2}}{w}=\frac{3}{2} \operatorname{cis}\left(-\frac{\pi}{12}\right)\)
- \(\frac{w}{z^{2}}=\frac{2}{3} \operatorname{cis}\left(\frac{\pi}{12}\right)\)
- \(\frac{z^{3}}{w^{2}}=\frac{3}{4} \operatorname{cis}(\pi)\)
- \(\frac{w^{2}}{z^{3}}=\frac{4}{3} \operatorname{cis}(\pi)\)
- \(\left(\frac{w}{z}\right)^{6}=64 \operatorname{cis}\left(-\frac{\pi}{2}\right)\)
- \((-2+2 i \sqrt{3})^{3}=64\)
- \((-\sqrt{3}-i)^{3}=-8 i\)
- \((-3+3 i)^{4}=-324\)
- \((\sqrt{3}+i)^{4}=-8+8 i \sqrt{3}\)
- \(\left(\frac{5}{2}+\frac{5}{2} i\right)^{3}=-\frac{125}{4}+\frac{125}{4} i\)
- \(\left(-\frac{1}{2}-\frac{i \sqrt{3}}{2}\right)^{6}=1\)
- \(\left(\frac{3}{2}-\frac{3}{2} i\right)^{3}=-\frac{27}{4}-\frac{27}{4} i\)
- \(\left(\frac{\sqrt{3}}{3}-\frac{1}{3} i\right)^{4}=-\frac{8}{81}-\frac{8 i \sqrt{3}}{81}\)
- \(\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i\right)^{4}=-1\)
- \((2+2 i)^{5}=-128-128 i\)
- \((\sqrt{3}-i)^{5}=-16 \sqrt{3}-16 i\)
- \((1-i)^{8}=16\)
- \(\begin{aligned}
&\text{Since }z=4 i=4 \operatorname{cis}\left(\frac{\pi}{2}\right)\text{ we have} \\
&w_{0}=2 \operatorname{cis}\left(\frac{\pi}{4}\right)=\sqrt{2}+i \sqrt{2} \quad\quad\quad\quad\quad w_{1}=2 \operatorname{cis}\left(\frac{5 \pi}{4}\right)=-\sqrt{2}-i \sqrt{2}
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=-25 i=25 \operatorname{cis}\left(\frac{3 \pi}{2}\right)\text{ we have}\\
&w_{0}=5 \operatorname{cis}\left(\frac{3 \pi}{4}\right)=-\frac{5 \sqrt{2}}{2}+\frac{5 \sqrt{2}}{2} i \quad\quad\quad\quad\quad w_{1}=5 \operatorname{cis}\left(\frac{7 \pi}{4}\right)=\frac{5 \sqrt{2}}{2}-\frac{5 \sqrt{2}}{2} i
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=1+i \sqrt{3}=2 \operatorname{cis}\left(\frac{\pi}{3}\right)\text{ we have}\\
&w_{0}=\sqrt{2} \operatorname{cis}\left(\frac{\pi}{6}\right)=\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2} i \quad\quad\quad\quad\quad w_{1}=\sqrt{2} \operatorname{cis}\left(\frac{7 \pi}{6}\right)=-\frac{\sqrt{6}}{2}-\frac{\sqrt{2}}{2} i
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=\frac{5}{2}-\frac{5 \sqrt{3}}{2} i=5 \operatorname{cis}\left(\frac{5 \pi}{3}\right)\text{ we have}\\
&w_{0}=\sqrt{5} \operatorname{cis}\left(\frac{5 \pi}{6}\right)=-\frac{\sqrt{15}}{2}+\frac{\sqrt{5}}{2} i \quad\quad\quad\quad\quad w_{1}=\sqrt{5} \operatorname{cis}\left(\frac{11 \pi}{6}\right)=\frac{\sqrt{15}}{2}-\frac{\sqrt{5}}{2} i
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=64=64 \operatorname{cis}(0)\text{ we have}\\
&w_{0}=4 \operatorname{cis}(0)=4 \quad\quad\quad\quad w_{1}=4 \operatorname{cis}\left(\frac{2 \pi}{3}\right)=-2+2 i \sqrt{3} \quad\quad\quad\quad w_{2}=4 \operatorname{cis}\left(\frac{4 \pi}{3}\right)=-2-2 i \sqrt{3}
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=-125=125 \operatorname{cis}(\pi)\text{ we have}\\
&w_{0}=5 \operatorname{cis}\left(\frac{\pi}{3}\right)=\frac{5}{2}+\frac{5 \sqrt{3}}{2} i \quad\quad\quad\quad w_{1}=5 \operatorname{cis}(\pi)=-5 \quad\quad\quad\quad w_{2}=5 \operatorname{cis}\left(\frac{5 \pi}{3}\right)=\frac{5}{2}-\frac{5 \sqrt{3}}{2} i
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=i=\operatorname{cis}\left(\frac{\pi}{2}\right)\text{ we have}\\
&w_{0}=\operatorname{cis}\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}+\frac{1}{2} i \quad\quad\quad\quad w_{1}=\operatorname{cis}\left(\frac{5 \pi}{6}\right)=-\frac{\sqrt{3}}{2}+\frac{1}{2} i \quad\quad\quad\quad w_{2}=\operatorname{cis}\left(\frac{3 \pi}{2}\right)=-i
\end{aligned}\) - \(\begin{aligned}
&\text{Since }z=-8 i=8 \operatorname{cis}\left(\frac{3 \pi}{2}\right)\text{ we have}\\
&w_{0}=2 \operatorname{cis}\left(\frac{\pi}{2}\right)=2 i \quad\quad\quad\quad w_{1}=2 \operatorname{cis}\left(\frac{7 \pi}{6}\right)=-\sqrt{3}-i \quad\quad\quad\quad w_{2}=\operatorname{cis}\left(\frac{11 \pi}{6}\right)=\sqrt{3}-i
\end{aligned}\) - \(\begin{array}{l}
&\text{Since }z=16=16 \operatorname{cis}(0)\text{ we have}&\\
&w_{0}=2 \operatorname{cis}(0)=2 & w_{1}=2 \operatorname{cis}\left(\frac{\pi}{2}\right)=2 i \\
&w_{2}=2 \operatorname{cis}(\pi)=-2 & w_{3}=2 \operatorname{cis}\left(\frac{3 \pi}{2}\right)=-2 i
\end{array}\) - \(\begin{array}{ll}
\text{Since }z=-81=81 \operatorname{cis}(\pi)\text{ we have}\\
w_{0}=3 \operatorname{cis}\left(\frac{\pi}{4}\right)=\frac{3 \sqrt{2}}{2}+\frac{3 \sqrt{2}}{2} i & w_{1}=3 \operatorname{cis}\left(\frac{3 \pi}{4}\right)=-\frac{3 \sqrt{2}}{2}+\frac{3 \sqrt{2}}{2} i \\
w_{2}=3 \operatorname{cis}\left(\frac{5 \pi}{4}\right)=-\frac{3 \sqrt{2}}{2}-\frac{3 \sqrt{2}}{2} i & w_{3}=3 \operatorname{cis}\left(\frac{7 \pi}{4}\right)=\frac{3 \sqrt{2}}{2}-\frac{3 \sqrt{2}}{2} i
\end{array}\) - \(\begin{array}{ll}
\text{Since }z=64=64 \operatorname{cis}(0)\text{ we have}\\
w_{0}=2 \operatorname{cis}(0)=2 & w_{1}=2 \operatorname{cis}\left(\frac{\pi}{3}\right)=1+\sqrt{3} i & w_{2}=2 \operatorname{cis}\left(\frac{2 \pi}{3}\right)=-1+\sqrt{3} i \\
w_{3}=2 \operatorname{cis}(\pi)=-2 & w_{4}=2 \operatorname{cis}\left(-\frac{2 \pi}{3}\right)=-1-\sqrt{3} i & w_{5}=2 \operatorname{cis}\left(-\frac{\pi}{3}\right)=1-\sqrt{3} i
\end{array}\) - \(\begin{array}{ll}
\text{Since }z=-729=729 \operatorname{cis}(\pi)\text{ we have}\\
w_{0}=3 \operatorname{cis}\left(\frac{\pi}{6}\right)=\frac{3 \sqrt{3}}{2}+\frac{3}{2} i & w_{1}=3 \operatorname{cis}\left(\frac{\pi}{2}\right)=3 i & w_{2}=3 \operatorname{cis}\left(\frac{5 \pi}{6}\right)=-\frac{3 \sqrt{3}}{2}+\frac{3}{2} i \\
w_{3}=3 \operatorname{cis}\left(\frac{7 \pi}{6}\right)=-\frac{3 \sqrt{3}}{2}-\frac{3}{2} i & w_{4}=3 \operatorname{cis}\left(-\frac{3 \pi}{2}\right)=-3 i & w_{5}=3 \operatorname{cis}\left(-\frac{11 \pi}{6}\right)=\frac{3 \sqrt{3}}{2}-\frac{3}{2} i
\end{array}\) - Note: In the answers for \(w_{0}\) and \(w_{2}\) the first rectangular form comes from applying the apporpriate Sum or Difference Identity \(\left(\frac{\pi}{12}=\frac{\pi}{3}-\frac{\pi}{4} \text { and } \frac{17 \pi}{12}=\frac{2 \pi}{3}+\frac{3 \pi}{4}, \text { respectively }\right)\) and the second comes from using the second comes from using the Half-Angle Identities.
\(w_{0}=\sqrt[3]{2} \operatorname{cis}\left(\frac{\pi}{12}\right)=\sqrt[3]{2}\left(\frac{\sqrt{6}+\sqrt{2}}{4}+i\left(\frac{\sqrt{6}-\sqrt{2}}{4}\right)\right)=\sqrt[3]{2}\left(\frac{\sqrt{2+\sqrt{3}}}{2}+i \frac{\sqrt{2-\sqrt{3}}}{2}\right)\)
\(w_{1}=\sqrt[3]{2} \operatorname{cis}\left(\frac{3 \pi}{4}\right)=\sqrt[3]{2}\left(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i\right)\)
\(w_{2}=\sqrt[3]{2} \operatorname{cis}\left(\frac{17 \pi}{12}\right)=\sqrt[3]{2}\left(\frac{\sqrt{2}-\sqrt{6}}{4}+i\left(\frac{-\sqrt{2}-\sqrt{6}}{4}\right)\right)=\sqrt[3]{2}\left(\frac{\sqrt{2-\sqrt{3}}}{2}+i \frac{\sqrt{2+\sqrt{3}}}{2}\right)\)
-
\(\begin{aligned}
&w_{0}=\operatorname{cis}(0)=1 \\
&w_{1}=\operatorname{cis}\left(\frac{2 \pi}{5}\right) \approx 0.309+0.951 i \\
&w_{2}=\operatorname{cis}\left(\frac{4 \pi}{5}\right) \approx-0.809+0.588 i \\
&w_{3}=\operatorname{cis}\left(\frac{6 \pi}{5}\right) \approx-0.809-0.588 i \\
&w_{4}=\operatorname{cis}\left(\frac{8 \pi}{5}\right) \approx 0.309-0.951 i
\end{aligned}\) - \(p(x)=x^{12}-4096=(x-2)(x+2)\left(x^{2}+4\right)\left(x^{2}-2 x+4\right)\left(x^{2}+2 x+4\right)\left(x^{2}-2 \sqrt{3} x+4\right)\left(x^{2}+2 \sqrt{3}+4\right)\)
Reference
1 ‘Well-defined’ means that no matter how we express \(z\), the number Re(\(z\)) is always the same, and the number Im(\(z\)) is always the same. In other words, Re and Im are functions of complex numbers.
2 In case you’re wondering, the use of the absolute value notation \(|z|\) for modulus will be explained shortly.
3 Recall the symbol being used here, '\(\in\),' is the mathematical symbol which denotes membership in a set.
4 If we had Calculus, we would regard \(\operatorname{Arg}(0)\) as an ‘indeterminate form.’ But we don’t, so we won’t.
5 Since the absolute value \(|x|\) of a real number \(x\) can be viewed as the distance from \(x\) to 0 on the number line, this first property justifies the notation \(|z|\) for modulus. We leave it to the reader to show that if \(z\) is real, then the definition of modulus coincides with absolute value so the notation \(|z|\) is unambiguous.
6 This may be considered by some to be a bit of a cheat, so we work through the underlying Algebra to see this is true. We know \(|z| = 0\) if and only if \(\sqrt{a^{2}+b^{2}}=0\) if and only if \(a^{2}+b^{2}=0\), which is true if and only if \(a = b = 0\). The latter happens if and only if \(z = a + bi = 0\). There.
7 See Example 3.4.1 in Section 3.4 for a review of complex number arithmetic.
8 See Section 9.3 for a review of this technique.
9 Compare this proof with the proof of the Power Rule in Theorem 11.14.
10 Assuming \(|w| > 1\).
11 Assuming \(\beta>0\).
12 Again, assuming \(|w|>1\).
13 Again, assuming \(\theta >0\).
14 For more on this, see the beautifully written epilogue to Section 3.4 found on page 294.


