11.6: Hooked on Conics Again

In this section, we revisit our friends the Conic Sections which we began studying in Chapter 7. Our first task is to formalize the notion of rotating axes so this subsection is actually a follow-up to Example 8.3.3 in Section 8.3. In that example, we saw that the graph of $y=\frac{2}{x}$ is actually a hyperbola. More specifically, it is the hyperbola obtained by rotating the graph of $x^{2}-y^{2}=4$ counter-clockwise through a $45^{\circ}$ angle. Armed with polar coordinates, we can generalize the process of rotating axes as shown below.

11.6.1 Rotation of Axes

Consider the $x-$ and $y$-axes below along with the dashed $x^{\prime}-$ and $y^{\prime}-$axes obtained by rotating the $x-$ and $y$-axes counter-clockwise through an angle $\theta$ and consider the point $P(x, y)$. The coordinates $(x, y)$ are rectangular coordinates and are based on the $x-$ and $y-$axes. Suppose we wished to find rectangular coordinates based on the $x^{\prime}-$ and $y^{\prime}-$axes. That is, we wish to determine $P\left(x^{\prime}, y^{\prime}\right)$. While this seems like a formidable challenge, it is nearly trivial if we use polar coordinates. Consider the angle $\phi$ whose initial side is the positive $x^{\prime}$-axis and whose terminal side contains the point $P$.

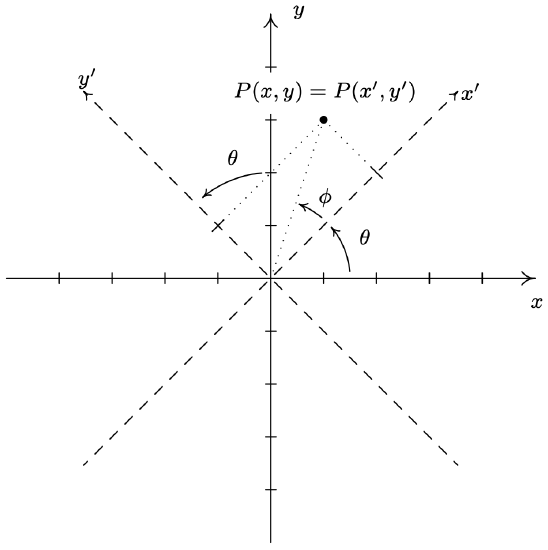
We relate $P(x, y)$ and $P\left(x^{\prime}, y^{\prime}\right)$ by converting them to polar coordinates. Converting $P(x, y)$ to polar coordinates with $r > 0$ yields $x=r \cos (\theta+\phi)$ and $y=r \sin (\theta+\phi)$. To convert the point $P\left(x^{\prime}, y^{\prime}\right)$ into polar coordinates, we first match the polar axis with the positive $x^{\prime}$-axis, choose the same $r > 0$ (since the origin is the same in both systems) and get $x^{\prime}=r \cos (\phi)$ and $y^{\prime}=r \sin (\phi)$. Using the sum formulas for sine and cosine, we have

$\begin{aligned} x &=r \cos (\theta+\phi) &\\ &=r \cos (\theta) \cos (\phi)-r \sin (\theta) \sin (\phi) &\quad \text { Sum formula for cosine } \\ &=(r \cos (\phi)) \cos (\theta)-(r \sin (\phi)) \sin (\theta)\\ &=x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta) &\quad \text { Since } x^{\prime}=r \cos (\phi) \text { and } y^{\prime}=r \sin (\phi) \end{aligned}$

Similarly, using the sum formula for sine we get $y=x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)$. These equations enable us to easily convert points with $x^{\prime} y^{\prime}$-coordinates back into $xy$-coordinates. They also enable us to easily convert equations in the variables $x$ and $y$ into equations in the variables in terms of $x^{\prime}$ and $y^{\prime}$.¹ If we want equations which enable us to convert points with $xy$-coordinates into $x^{\prime} y^{\prime}$-coordinates, we need to solve the system

$\left\{\begin{array}{l} x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta)=x \\ x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)=y \end{array}\right.$

for $x^{\prime}$ and $y^{\prime}$. Perhaps the cleanest way² to solve this system is to write it as a matrix equation. Using the machinery developed in Section 8.4, we write the above system as the matrix equation $A X^{\prime}=X$ where

$A=\left[\begin{array}{rr} \cos (\theta) & -\sin (\theta) \\ \sin (\theta) & \cos (\theta) \end{array}\right], \quad X^{\prime}=\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right], \quad X=\left[\begin{array}{l} x \\ y \end{array}\right]$

Since $\operatorname{det}(A)=(\cos (\theta))(\cos (\theta))-(-\sin (\theta))(\sin (\theta))=\cos ^{2}(\theta)+\sin ^{2}(\theta)=1$, the determinant of $A$ is not zero so $A$ is invertible and $X^{\prime}=A^{-1} X$. Using the formula given in Equation 8.2 with $\operatorname{det}(A)=1$, we find

$A^{-1}=\left[\begin{array}{rr} \cos (\theta) & \sin (\theta) \\ -\sin (\theta) & \cos (\theta) \end{array}\right]$

so that

$\begin{aligned} X^{\prime} &=A^{-1} X \\ {\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right] } &=\left[\begin{array}{rr} \cos (\theta) & \sin (\theta) \\ -\sin (\theta) & \cos (\theta) \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] \\ {\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right] } &=\left[\begin{array}{c} x \cos (\theta)+y \sin (\theta) \\ -x \sin (\theta)+y \cos (\theta) \end{array}\right] \end{aligned}$

From which we get $x^{\prime}=x \cos (\theta)+y \sin (\theta)$ and $y^{\prime}=-x \sin (\theta)+y \cos (\theta)$. To summarize,

Theorem 11.9. Rotation of Axes

Suppose the positive $x$ and $y$ axes are rotated counterclockwise through an angle $\theta$ to produce the axes $x^{\prime}$ and $y^{\prime}$, respectively. Then the coordinates $P(x, y)$ and $P\left(x^{\prime}, y^{\prime}\right)$ are related by the following systems of equations

$\left\{\begin{array} { l } { x = x ^ { \prime } \operatorname { c o s } ( \theta ) - y ^ { \prime } \operatorname { s i n } ( \theta ) } \\ { y = x ^ { \prime } \operatorname { s i n } ( \theta ) + y ^ { \prime } \operatorname { c o s } ( \theta ) } \end{array} \quad \text { and } \quad \left\{\begin{array}{l} x^{\prime}=x \cos (\theta)+y \sin (\theta) \\ y^{\prime}=-x \sin (\theta)+y \cos (\theta) \end{array}\right.\right.$

We put the formulas in Theorem 11.9 to good use in the following example.

Example 11.6.1

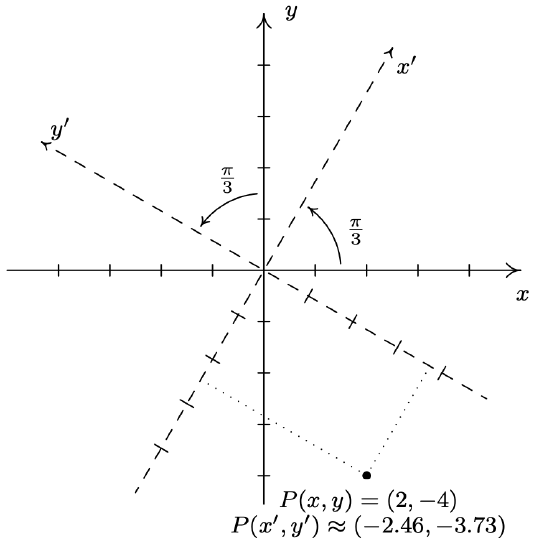
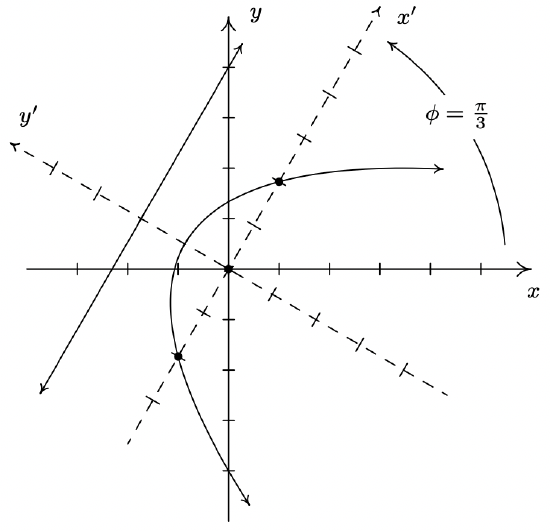
Suppose the $x-$ and $y-$ axes are both rotated counter-clockwise through the angle $\theta=\frac{\pi}{3}$ to produce the $x^{\prime}-$ and $y^{\prime}-$axes, respectively.

1. Let $P(x, y) = (2, −4)$ and find $P\left(x^{\prime}, y^{\prime}\right)$. Check your answer algebraically and graphically.
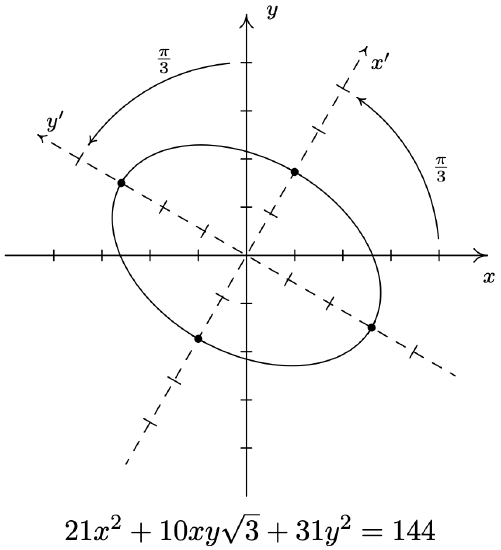
2. Convert the equation $21 x^{2}+10 x y \sqrt{3}+31 y^{2}=144$ to an equation in $x^{\prime}$ and $y^{\prime}$ and graph.

Solution

1. If $P(x, y) = (2, −4)$ then $x = 2$ and $y = −4$. Using these values for $x$ and $y$ along with $\theta=\frac{\pi}{3}$, Theorem 11.9 gives $x^{\prime}=x \cos (\theta)+y \sin (\theta)=2 \cos \left(\frac{\pi}{3}\right)+(-4) \sin \left(\frac{\pi}{3}\right)$ which simplifies $x^{\prime}=1-2 \sqrt{3}$. Similarly, $y^{\prime}=-x \sin (\theta)+y \cos (\theta)=(-2) \sin \left(\frac{\pi}{3}\right)+(-4) \cos \left(\frac{\pi}{3}\right)$ which gives $y^{\prime}=-\sqrt{3}-2=-2-\sqrt{3}$. Hence $P\left(x^{\prime}, y^{\prime}\right)=(1-2 \sqrt{3},-2-\sqrt{3})$. To check our answer algebraically, we use the formulas in Theorem 11.9 to convert $P\left(x^{\prime}, y^{\prime}\right)=(1-2 \sqrt{3},-2-\sqrt{3})$ back into $x$ and $y$ coordinates. We get

   $\begin{aligned} x &=x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta) \\ &=(1-2 \sqrt{3}) \cos \left(\frac{\pi}{3}\right)-(-2-\sqrt{3}) \sin \left(\frac{\pi}{3}\right) \\ &=\left(\frac{1}{2}-\sqrt{3}\right)-\left(-\sqrt{3}-\frac{3}{2}\right) \\ &=2 \end{aligned}$

   Similarly, using $y=x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)$, we obtain $y = −4$ as required. To check our answer graphically, we sketch in the $x^{\prime} \text {-axis }$ and $y^{\prime} \text {-axis }$ to see if the new coordinates $P(x^{\prime},y^{\prime})=(1-2 \sqrt{3},-2-\sqrt{3}) \approx(-2.46,-3.73)$ seem reasonable. Our graph is below.

   

2. To convert the equation $21 x^{2}+10 x y \sqrt{3}+31 y^{2}=144$ to an equation in the variables $x^{\prime}$ and $y^{\prime}$, we substitute $x=x^{\prime} \cos \left(\frac{\pi}{3}\right)-y^{\prime} \sin \left(\frac{\pi}{3}\right)=\frac{x^{\prime}}{2}-\frac{y^{\prime} \sqrt{3}}{2}$ and $y=x^{\prime} \sin \left(\frac{\pi}{3}\right)+y^{\prime} \cos \left(\frac{\pi}{3}\right)=\frac{x^{\prime} \sqrt{3}}{2}+\frac{y^{\prime}}{2}$ and simplify. While this is by no means a trivial task, it is nothing more than a hefty dose of Beginning Algebra. We will not go through the entire computation, but rather, the reader should take the time to do it. Start by verifying that

   $x^{2}=\frac{\left(x^{\prime}\right)^{2}}{4}-\frac{x^{\prime} y^{\prime} \sqrt{3}}{2}+\frac{3\left(y^{\prime}\right)^{2}}{4}, \quad x y=\frac{\left(x^{\prime}\right)^{2} \sqrt{3}}{4}-\frac{x^{\prime} y^{\prime}}{2}-\frac{\left(y^{\prime}\right)^{2} \sqrt{3}}{4}, \quad y^{2}=\frac{3\left(x^{\prime}\right)^{2}}{4}+\frac{x^{\prime} y^{\prime} \sqrt{3}}{2}+\frac{\left(y^{\prime}\right)^{2}}{4}$

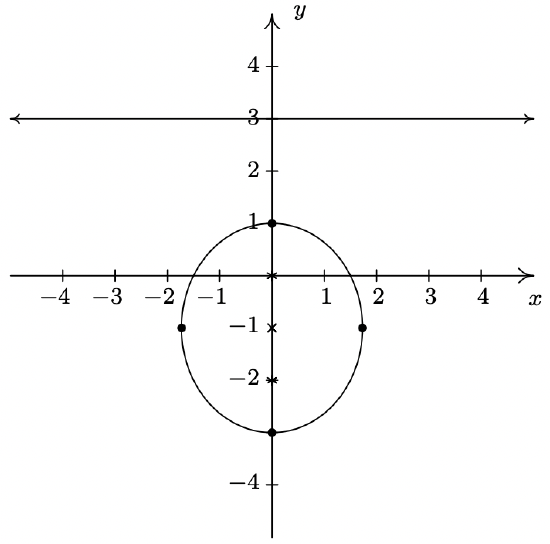
   To our surprise and delight, the equation $21 x^{2}+10 x y \sqrt{3}+31 y^{2}=144$ in $xy$-coordinates reduces to $36\left(x^{\prime}\right)^{2}+16\left(y^{\prime}\right)^{2}=144$, or $\frac{\left(x^{\prime}\right)^{2}}{4}+\frac{\left(y^{\prime}\right)^{2}}{9}=1$ in $x^{\prime} y^{\prime}$-coordinates. The latter is an ellipse centered at (0, 0) with vertices along the $y^{\prime}$-axis with ($x^{\prime} y^{\prime}$-coordinates) $(0, \pm 3)$ and whose minor axis has endpoints with ($x^{\prime} y^{\prime}$-coordinates) $(\pm 2,0)$. We graph it below.

   

The elimination of the troublesome ‘$xy$’ term from the equation $21 x^{2}+10 x y \sqrt{3}+31 y^{2}=144$ in Example 11.6.1 number 2 allowed us to graph the equation by hand using what we learned in Chapter 7. It is natural to wonder if we can always do this. That is, given an equation of the form $A x^{2}+B x y+C y^{2}+D x+E y+F=0$, with $B \neq 0$, is there an angle $\theta$ so that if we rotate the $x$ and $y$-axes counter-clockwise through that angle $\theta$, the equation in the rotated variables $x^{\prime}$ and $y^{\prime}$ contains no $x^{\prime} y^{\prime}$ term? To explore this conjecture, we make the usual substitutions $x=x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta)$ and $y=x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)$ into the equation $A x^{2}+B x y+C y^{2}+D x+E y+F=0$ and set the coefficient of the $x^{\prime} y^{\prime}$ term equal to 0. Terms containing $x^{\prime} y^{\prime}$ in this expression will come from the first three terms of the equation: $A x^{2}$, $B x y$ and $C y^{2}$. We leave it to the reader to verify that

$\begin{aligned} x^{2} &=\left(x^{\prime}\right)^{2} \cos ^{2}(\theta)-2 x^{\prime} y^{\prime} \cos (\theta) \sin (\theta)+\left(y^{\prime}\right)^{2} \sin (\theta) \\ x y &=\left(x^{\prime}\right)^{2} \cos (\theta) \sin (\theta)+x^{\prime} y^{\prime}\left(\cos ^{2}(\theta)-\sin ^{2}(\theta)\right)-\left(y^{\prime}\right)^{2} \cos (\theta) \sin (\theta) \\ y^{2} &=\left(x^{\prime}\right)^{2} \sin ^{2}(\theta)+2 x^{\prime} y^{\prime} \cos (\theta) \sin (\theta)+\left(y^{\prime}\right)^{2} \cos ^{2}(\theta) \end{aligned}$

The contribution to the $x^{\prime} y^{\prime}$-term from $A x^{2}$ is $-2 A \cos (\theta) \sin (\theta)$, from $Bxy$ it is $B\left(\cos ^{2}(\theta)-\sin ^{2}(\theta)\right)$, and from $C y^{2}$ it is $2 C \cos (\theta) \sin (\theta)$. Equating the $x^{\prime} y^{\prime}$-term to 0, we get

$\begin{aligned} -2 A \cos (\theta) \sin (\theta)+B\left(\cos ^{2}(\theta)-\sin ^{2}(\theta)\right)+2 C \cos (\theta) \sin (\theta) &=0 \\ -A \sin (2 \theta)+B \cos (2 \theta)+C \sin (2 \theta) &=0 \quad \text { Double Angle Identities } \end{aligned}$

From this, we get $B \cos (2 \theta)=(A-C) \sin (2 \theta)$, and our goal is to solve for $\theta$ in terms of the coefficients $A$, $B$ and $C$. Since we are assuming $B \neq 0$, we can divide both sides of this equation by $B$. To solve for $\theta$ we would like to divide both sides of the equation by $\sin (2 \theta)$, provided of course that we have assurances that $\sin (2 \theta) \neq 0$. If $\sin (2 \theta)=0$, then we would have $B \cos (2 \theta)=0$, and since $B \neq 0$, this would force $\cos (2 \theta)=0$. Since no angle $\theta$ can have both $\sin (2 \theta)=0$ and $\cos (2 \theta)=0$, we can safely assume³ $\sin (2 \theta) \neq 0$. We get $\frac{\cos (2 \theta)}{\sin (2 \theta)}=\frac{A-C}{B}$, or $\cot (2 \theta)=\frac{A-C}{B}$. We have just proved the following theorem.

Theorem 11.10

The equation $A x^{2}+B x y+C y^{2}+D x+E y+F=0$ with $B \neq 0$ can be transformed into an equation in variables $x^{\prime}$ and $y^{\prime}$ without any $x^{\prime} y^{\prime}$ terms by rotating the $x-$ and $y-$ axes counter-clockwise through an angle $\theta$ which satisfies $\cot (2 \theta)=\frac{A-C}{B}$.

We put Theorem 11.10 to good use in the following example.

Example 11.6.2

Graph the following equations.

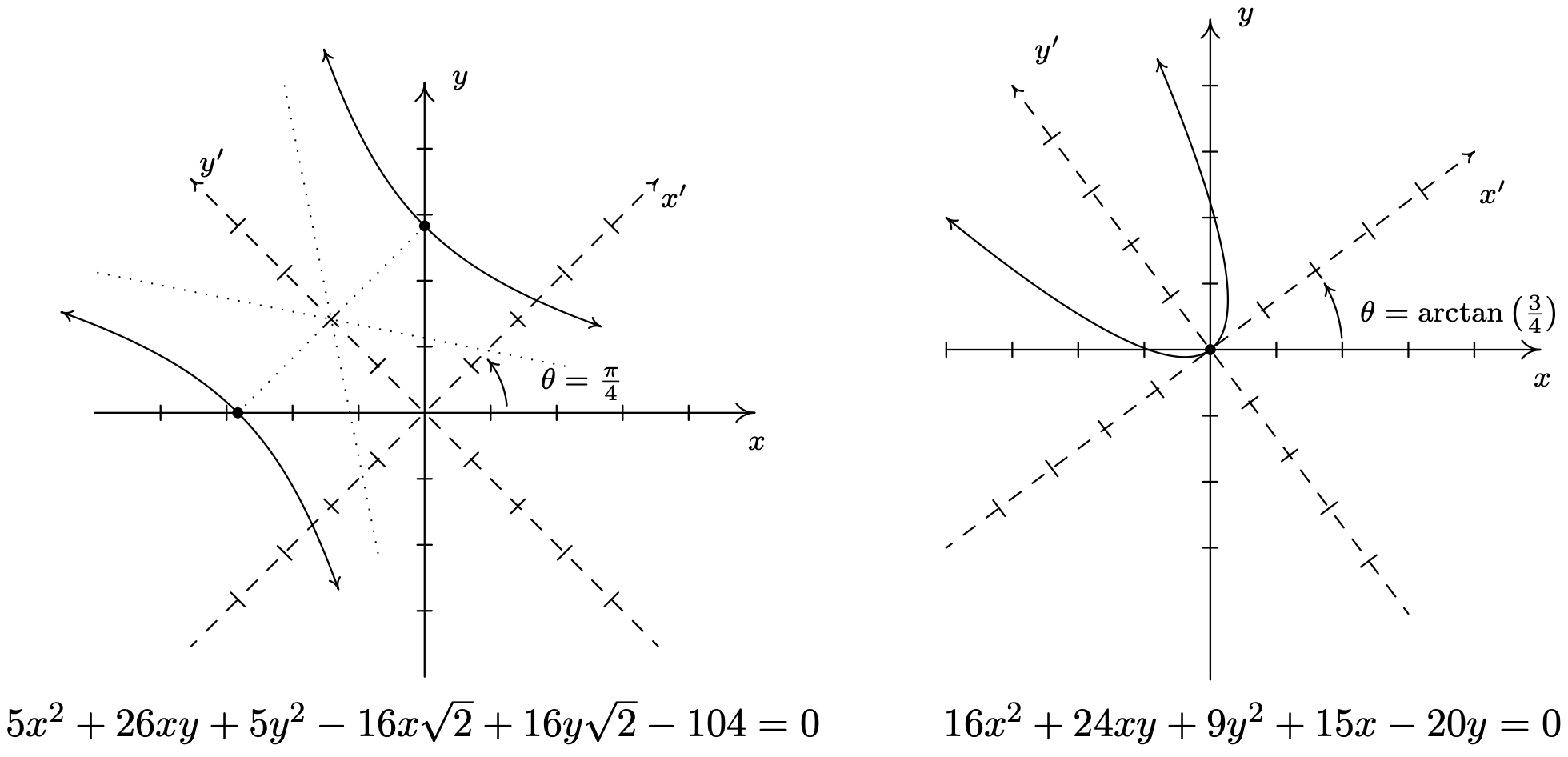
1. $5 x^{2}+26 x y+5 y^{2}-16 x \sqrt{2}+16 y \sqrt{2}-104=0$
2. $16 x^{2}+24 x y+9 y^{2}+15 x-20 y=0$

Solution

1. Since the equation $5 x^{2}+26 x y+5 y^{2}-16 x \sqrt{2}+16 y \sqrt{2}-104=0$ is already given to us in the form required by Theorem 11.10, we identify $A = 5$, $B = 26$ and $C = 5$ so that $\cot (2 \theta)=\frac{A-C}{B}=\frac{5-5}{26}=0$. This means $\cot (2 \theta)=0$ which gives $\theta=\frac{\pi}{4}+\frac{\pi}{2} k$ for integers $k$. We choose $\theta=\frac{\pi}{4}$ so that our rotation equations are $x=\frac{x^{\prime} \sqrt{2}}{2}-\frac{y^{\prime} \sqrt{2}}{2}$ and $y=\frac{x^{\prime} \sqrt{2}}{2}+\frac{y^{\prime} \sqrt{2}}{2}$. The reader should verify that

   $x^{2}=\frac{\left(x^{\prime}\right)^{2}}{2}-x^{\prime} y^{\prime}+\frac{\left(y^{\prime}\right)^{2}}{2}, \quad x y=\frac{\left(x^{\prime}\right)^{2}}{2}-\frac{\left(y^{\prime}\right)^{2}}{2}, \quad y^{2}=\frac{\left(x^{\prime}\right)^{2}}{2}+x^{\prime} y^{\prime}+\frac{\left(y^{\prime}\right)^{2}}{2}$

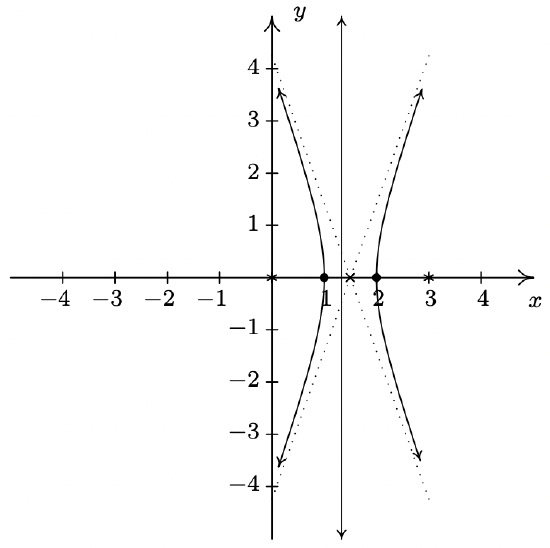
   Making the other substitutions, we get that $5 x^{2}+26 x y+5 y^{2}-16 x \sqrt{2}+16 y \sqrt{2}-104=0$ reduces to $18\left(x^{\prime}\right)^{2}-8\left(y^{\prime}\right)^{2}+32 y^{\prime}-104=0$, or $\frac{\left(x^{\prime}\right)^{2}}{4}-\frac{\left(y^{\prime}-2\right)^{2}}{9}=1$. The latter is the equation of a hyperbola centered at the $x^{\prime} y^{\prime}$-coordinates $(0,2)$ opening in the $x^{\prime}$ direction with vertices $(\pm 2,2)$ (in $x^{\prime} y^{\prime}$-coordinates) and asymptotes $y^{\prime}=\pm \frac{3}{2} x^{\prime}+2$. We graph it below.

2. From $16 x^{2}+24 x y+9 y^{2}+15 x-20 y=0$, we get $A = 16$, $B = 24$ and $C = 9$ so that $\cot (2 \theta)=\frac{7}{24}$. Since this isn’t one of the values of the common angles, we will need to use inverse functions. Ultimately, we need to find $\cos (\theta)$ and $\sin (\theta)$, which means we have two options. If we use the arccotangent function immediately, after the usual calculations we get $\theta=\frac{1}{2} \operatorname{arccot}\left(\frac{7}{24}\right)$. To get $\cos (\theta)$ and $\sin (\theta)$ from this, we would need to use half angle identities. Alternatively, we can start with $\cot (2 \theta)=\frac{7}{24}$, use a double angle identity, and then go after $\cos (\theta)$ and $\sin (\theta)$. We adopt the second approach. From $\cot (2 \theta)=\frac{7}{24}$, we have $\tan (2 \theta)=\frac{24}{7}$. Using the double angle identity for tangent, we have $\frac{2 \tan (\theta)}{1-\tan ^{2}(\theta)}=\frac{24}{7}$, which give $24 \tan ^{2}(\theta)+14 \tan (\theta)-24=0$. Factoring, we get $2(3 \tan (\theta)+4)(4 \tan (\theta)-3)=0$ which gives $\tan (\theta)=-\frac{4}{3}$ or $\tan (\theta)=\frac{3}{4}$. While either of these values of $\tan (\theta)$ satisfies the equation $\cot (2 \theta)=\frac{7}{24}$, we choose $\tan (\theta)=\frac{3}{4}$, since this produces an acute angle,⁴ $\theta=\arctan \left(\frac{3}{4}\right)$. To find the rotation equations, we need $\cos (\theta)=\cos \left(\arctan \left(\frac{3}{4}\right)\right)$ and $\sin (\theta)=\sin \left(\arctan \left(\frac{3}{4}\right)\right)$. Using the techniques developed in Section 10.6 we get $\cos (\theta)=\frac{4}{5} \text { and } \sin (\theta)=\frac{3}{5}$. Our rotation equations are $x=x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta)=\frac{4 x^{\prime}}{5}-\frac{3 y^{\prime}}{5}$ and $y=x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)=\frac{3 x^{\prime}}{5}+\frac{4 y^{\prime}}{5}$. As usual, we now substitute these quantities into $16 x^{2}+24 x y+9 y^{2}+15 x-20 y=0$ and simplify. As a first step, the reader can verify

   $x^{2}=\frac{16\left(x^{\prime}\right)^{2}}{25}-\frac{24 x^{\prime} y^{\prime}}{25}+\frac{9\left(y^{\prime}\right)^{2}}{25}, \quad x y=\frac{12\left(x^{\prime}\right)^{2}}{25}+\frac{7 x^{\prime} y^{\prime}}{25}-\frac{12\left(y^{\prime}\right)^{2}}{25}, \quad y^{2}=\frac{9\left(x^{\prime}\right)^{2}}{25}+\frac{24 x^{\prime} y^{\prime}}{25}+\frac{16\left(y^{\prime}\right)^{2}}{25}$

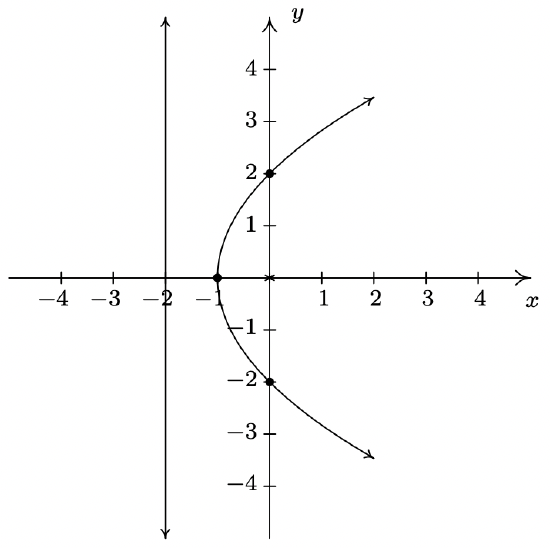
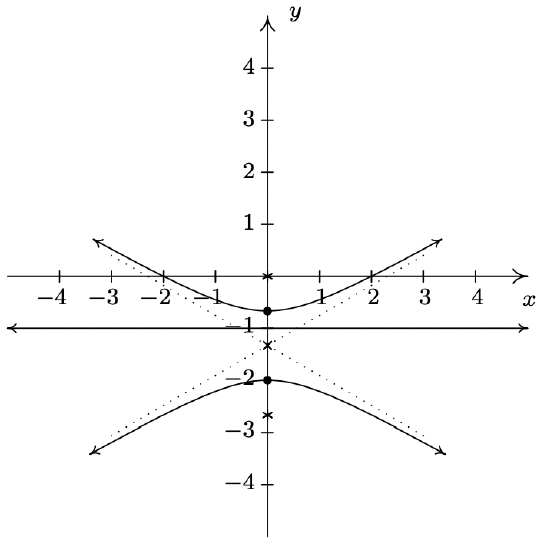
   Once the dust settles, we get $25\left(x^{\prime}\right)^{2}-25 y^{\prime}=0, \text { or } y^{\prime}=\left(x^{\prime}\right)^{2}$, whose graph is a parabola opening along the positive $y^{\prime}$-axis with vertex (0, 0). We graph this equation below.

   

We note that even though the coefficients of $x^{2}$ and $y^{2}$ were both positive numbers in parts 1 and 2 of Example 11.6.2, the graph in part 1 turned out to be a hyperbola and the graph in part 2 worked out to be a parabola. Whereas in Chapter 7, we could easily pick out which conic section we were dealing with based on the presence (or absence) of quadratic terms and their coefficients, Example 11.6.2 demonstrates that all bets are off when it comes to conics with an xy term which require rotation of axes to put them into a more standard form. Nevertheless, it is possible to determine which conic section we have by looking at a special, familiar combination of the coefficients of the quadratic terms. We have the following theorem.

Theorem 11.11

Suppose the equation $A x^{2}+B x y+C y^{2}+D x+E y+F=0$ describes a non-degenerate conic section.^a

• If $B^{2}-4 A C>0$ then the graph of the equation is a hyperbola.
• If $B^{2}-4 A C=0$ then the graph of the equation is a parabola.
• If $B^{2}-4 A C<0$ then the graph of the equation is an ellipse or circle.

---

^a Recall that this means its graph is either a circle, parabola, ellipse or hyperbola. See page 497.

As you may expect, the quantity $B^{2}-4 A C$ mentioned in Theorem 11.11 is called the discriminant of the conic section. While we will not attempt to explain the deep Mathematics which produces this ‘coincidence’, we will at least work through the proof of Theorem 11.11 mechanically to show that it is true.⁵ First note that if the coefficient $B = 0$ in the equation $A x^{2}+B x y+C y^{2}+D x+E y+F=0$, Theorem 11.11 reduces to the result presented in Exercise 34 in Section 7.5, so we proceed here under the assumption that $B \neq 0$. We rotate the $xy$-axes counter-clockwise through an angle $\theta$ which satisfies $\cot (2 \theta)=\frac{A-C}{R}$ to produce an equation with no $x^{\prime} y^{\prime}$-term in accordance with Theorem 11.10: $A^{\prime}\left(x^{\prime}\right)^{2}+C\left(y^{\prime}\right)^{2}+D x^{\prime}+E y^{\prime}+F^{\prime}=0$. In this form, we can invoke Exercise 34 in Section 7.5 once more using the product $A^{\prime} C^{\prime}$. Our goal is to find the product $A^{\prime} C^{\prime}$ in terms of the coefficients $A$, $B$ and $C$ in the original equation. To that end, we make the usual substitutions $x=x^{\prime} \cos (\theta)-y^{\prime} \sin (\theta) y=x^{\prime} \sin (\theta)+y^{\prime} \cos (\theta)$ into $A x^{2}+B x y+C y^{2}+D x+E y+F=0$. We leave it to the reader to show that, after gathering like terms, the coefficient $A^{\prime}$ on $\left(x^{\prime}\right)^{2}$ and the coefficient $C^{\prime}$ on $\left(y^{\prime}\right)^{2}$ are

$\begin{aligned} &A^{\prime}=A \cos ^{2}(\theta)+B \cos (\theta) \sin (\theta)+C \sin ^{2}(\theta) \\ &C^{\prime}=A \sin ^{2}(\theta)-B \cos (\theta) \sin (\theta)+C \cos ^{2}(\theta) \end{aligned}$

In order to make use of the condition $\cot (2 \theta)=\frac{A-C}{B}$, we rewrite our formulas for $A^{\prime}$ and $C^{\prime}$ using the power reduction formulas. After some regrouping, we get

$\begin{aligned} &2 A^{\prime}=[(A+C)+(A-C) \cos (2 \theta)]+B \sin (2 \theta) \\ &2 C^{\prime}=[(A+C)-(A-C) \cos (2 \theta)]-B \sin (2 \theta) \end{aligned}$

Next, we try to make sense of the product

$\left(2 A^{\prime}\right)\left(2 C^{\prime}\right)=\{[(A+C)+(A-C) \cos (2 \theta)]+B \sin (2 \theta)\}\{[(A+C)-(A-C) \cos (2 \theta)]-B \sin (2 \theta)\}$

We break this product into pieces. First, we use the difference of squares to multiply the ‘first’ quantities in each factor to get

$[(A+C)+(A-C) \cos (2 \theta)][(A+C)-(A-C) \cos (2 \theta)]=(A+C)^{2}-(A-C)^{2} \cos ^{2}(2 \theta)$

Next, we add the product of the ‘outer’ and ‘inner’ quantities in each factor to get

$\begin{aligned} &-B \sin (2 \theta)[(A+C)+(A-C) \cos (2 \theta)] \\ &+B \sin (2 \theta)[(A+C)-(A-C) \cos (2 \theta)]=-2 B(A-C) \cos (2 \theta) \sin (2 \theta) \end{aligned}$

The product of the ‘last’ quantity in each factor is $(B \sin (2 \theta))(-B \sin (2 \theta))=-B^{2} \sin ^{2}(2 \theta)$. Putting all of this together yields

$4 A^{\prime} C^{\prime}=(A+C)^{2}-(A-C)^{2} \cos ^{2}(2 \theta)-2 B(A-C) \cos (2 \theta) \sin (2 \theta)-B^{2} \sin ^{2}(2 \theta)$

From $\cot (2 \theta)=\frac{A-C}{B}$, we get $\frac{\cos (2 \theta)}{\sin (2 \theta)}=\frac{A-C}{B}$, or $(A-C) \sin (2 \theta)=B \cos (2 \theta)$. We use this substitution twice along with the Pythagorean Identity $\cos ^{2}(2 \theta)=1-\sin ^{2}(2 \theta)$ to get

$\begin{aligned} 4 A^{\prime} C^{\prime} &=(A+C)^{2}-(A-C)^{2} \cos ^{2}(2 \theta)-2 B(A-C) \cos (2 \theta) \sin (2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}\left[1-\sin ^{2}(2 \theta)\right]-2 B \cos (2 \theta) B \cos (2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}+(A-C)^{2} \sin ^{2}(2 \theta)-2 B^{2} \cos ^{2}(2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}+[(A-C) \sin (2 \theta)]^{2}-2 B^{2} \cos ^{2}(2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}+[B \cos (2 \theta)]^{2}-2 B^{2} \cos ^{2}(2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}+B^{2} \cos ^{2}(2 \theta)-2 B^{2} \cos ^{2}(2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}-B^{2} \cos ^{2}(2 \theta)-B^{2} \sin ^{2}(2 \theta) \\ &=(A+C)^{2}-(A-C)^{2}-B^{2}\left[\cos ^{2}(2 \theta)+\sin ^{2}(2 \theta)\right] \\ &=(A+C)^{2}-(A-C)^{2}-B^{2} \\ &=\left(A^{2}+2 A C+C A^{2}\right)\left(A^{2}-2 A C+C^{2}\right)-B^{2} \\ &=4 A C-B^{2} \end{aligned}$

Hence, $B^{2}-4 A C=-4 A^{\prime} C^{\prime}$, so the quantity $B^{2}-4 A C$ has the opposite sign of $A^{\prime} C^{\prime}$. . The result now follows by applying Exercise 34 in Section 7.5.

Example 11.6.3

Use Theorem 11.11 to classify the graphs of the following non-degenerate conics.

1. $21 x^{2}+10 x y \sqrt{3}+31 y^{2}=144$
2. $5 x^{2}+26 x y+5 y^{2}-16 x \sqrt{2}+16 y \sqrt{2}-104=0$
3. $16 x^{2}+24 x y+9 y^{2}+15 x-20 y=0$

Solution

This is a straightforward application of Theorem 11.11.

1. We have $A=21, B=10 \sqrt{3}$ and $C=31 \text { so } B^{2}-4 A C=(10 \sqrt{3})^{2}-4(21)(31)=-2304<0$. Theorem 11.11 predicts the graph is an ellipse, which checks with our work from Example 11.6.1 number 2.
2. Here, $A = 5$, $B = 26$ and $C = 5$, so $B^{2}-4 A C=26^{2}-4(5)(5)=576>0$. Theorem 11.11 classifies the graph as a hyperbola, which matches our answer to Example 11.6.2 number 1.
3. Finally, we have $A = 16, B = 24$ and $C = 9$ which gives $24^{2}-4(16)(9)=0$. Theorem 11.11 tells us that the graph is a parabola, matching our result from Example 11.6.2 number 2.

11.6.2 The Polar Form of Conics

In this subsection, we start from scratch to reintroduce the conic sections from a more unified perspective. We have our ‘new’ definition below.

Definition 11.1

Given a fixed line $L$, a point $F$ not on $L$, and a positive number $e$, a conic section is the set of all points $P$ such that

$\frac{\text { the distance from } P \text { to } F}{\text { the distance from } P \text { to } L}=e$

The line $L$ is called the directrix of the conic section, the point $F$ is called a focus of the conic section, and the constant $e$ is called the eccentricity of the conic section.

We have seen the notions of focus and directrix before in the definition of a parabola, Definition 7.3. There, a parabola is defined as the set of points equidistant from the focus and directrix, giving an eccentricity $e = 1$ according to Definition 11.1. We have also seen the concept of eccentricity before. It was introduced for ellipses in Definition 7.5 in Section 7.4, and later extended to hyperbolas in Exercise 31 in Section 7.5. There, $e$ was also defined as a ratio of distances, though in these cases the distances involved were measurements from the center to a focus and from the center to a vertex. One way to reconcile the ‘old’ ideas of focus, directrix and eccentricity with the ‘new’ ones presented in Definition 11.1 is to derive equations for the conic sections using Definition 11.1 and compare these parameters with what we know from Chapter 7. We begin by assuming the conic section has eccentricity $e$, a focus $F$ at the origin and that the directrix is the vertical line $x = −d$ as in the figure below.

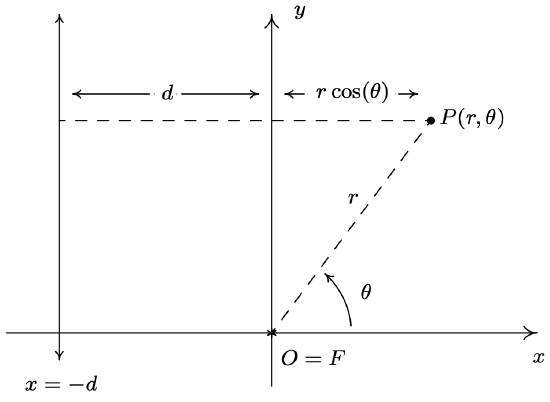
Using a polar coordinate representation $P(r, \theta)$ for a point on the conic with $r > 0$, we get

$e=\frac{\text { the distance from } P \text { to } F}{\text { the distance from } P \text { to } L}=\frac{r}{d+r \cos (\theta)}$

so that $r=e(d+r \cos (\theta))$. Solving this equation for $r$, yields

$r=\frac{e d}{1-e \cos (\theta)}$

At this point, we convert the equation $r=e(d+r \cos (\theta))$ back into a rectangular equation in the variables $x$ and $y$. If $e > 0$, but $e \neq 1$, the usual conversion process outlined in Section 11.4 gives⁶

$\left(\frac{\left(1-e^{2}\right)^{2}}{e^{2} d^{2}}\right)\left(x-\frac{e^{2} d}{1-e^{2}}\right)^{2}+\left(\frac{1-e^{2}}{e^{2} d^{2}}\right) y^{2}=1$

We leave it to the reader to show if $0 < e < 1$, this is the equation of an ellipse centered a $\left(\frac{e^{2} d}{1-e^{2}}, 0\right)$ with major axis along the $x$-axis. Using the notation from Section 7.4, we have $a^2=\frac{e^{2} d^2}{(1-e^{2})^2}$ and $b^{2}=\frac{e^{2} d^{2}}{1-e^{2}}$, so the major axis has length $\frac{2 e d}{1-e^{2}}$ and the minor axis has length $\frac{2 e d}{\sqrt{1-e^{2}}}$. Moreover, we find that one focus is (0, 0) and working through the formula given in Definition 7.5 gives the eccentricity to be $e$, as required. If $e > 1$, then the equation generates a hyperbola with center $\left(\frac{e^{2} d}{1-e^{2}}, 0\right)$ whose transverse axis lies along the $x$-axis. Since such hyperbolas have the for $\frac{(x-h)^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, we need to take the opposite reciprocal of the coefficient of $y^{2}$ to find $b^{2}$. We get⁷ $a^{2}=\frac{e^{2} d^{2}}{\left(1-e^{2}\right)^{2}}=\frac{e^{2} d^{2}}{\left(e^{2}-1\right)^{2}}$ and $b^{2}=-\frac{e^{2} d^{2}}{1-e^{2}}=\frac{e^{2} d^{2}}{e^{2}-1}$, so the transverse axis has length $\frac{2 e d}{e^{2}-1}$ and the conjugate axis has length $\frac{2 e d}{\sqrt{e^{2}-1}}$. Additionally, we verify that one focus is at (0, 0), and the formula given in Exercise 31 in Section 7.5 gives the eccentricity is e in this case as well. If $e = 1$, the equation $r=\frac{e d}{1-e \cos (\theta)}$ reduces to $r=\frac{d}{1-\cos (\theta)}$ which gives the rectangular equation $y^{2}=2 d\left(x+\frac{d}{2}\right)$. This is a parabola with vertex $\left(-\frac{d}{2}, 0\right)$ opening to the right. In the language of Section 7.3, $4p = 2d$ so $p=\frac{d}{2}$, the focus is (0, 0), the focal diameter is $2d$ and the directrix is $x = −d$, as required. Hence, we have shown that in all cases, our ‘new’ understanding of ‘conic section’, ‘focus’, ‘eccentricity’ and ‘directrix’ as presented in Definition 11.1 correspond with the ‘old’ definitions given in Chapter 7.

Before we summarize our findings, we note that in order to arrive at our general equation of a conic $r=\frac{e d}{1-e \cos (\theta)}$, we assumed that the directrix was the line $x = −d$ for $d > 0$. We could have just as easily chosen the directrix to be $x = d, y = −d$ or $y = d$. As the reader can verify, in these cases we obtain the forms $r=\frac{e d}{1+e \cos (\theta)}, r=\frac{e d}{1-e \sin (\theta)} \text { and } r=\frac{e d}{1+e \sin (\theta)}$, respectively. The key thing to remember is that in any of these cases, the directrix is always perpendicular to the major axis of an ellipse and it is always perpendicular to the transverse axis of the hyperbola. For parabolas, knowing the focus is (0, 0) and the directrix also tells us which way the parabola opens. We have established the following theorem.

Theorem 11.12

Suppose $e$ and $d$ are positive numbers. Then

• the graph of $r=\frac{e d}{1-e \cos (\theta)}$ is the graph of a conic section with directrix $x = −d$.
• the graph of $r=\frac{e d}{1+e \cos (\theta)}$ is the graph of a conic section with directrix $x = d$.
• the graph of $r=\frac{e d}{1-e \sin (\theta)}$ is the graph of a conic section with directrix $y = −d$.
• the graph of $r=\frac{e d}{1+e \sin (\theta)}$ is the graph of a conic section with directrix $y = d$.

In each case above, (0, 0) is a focus of the conic and the number $e$ is the eccentricity of the conic.

• If $0 < e < 1$, the graph is an ellipse whose major axis has length $\frac{2 e d}{1-e^{2}}$ and whose minor axis has length $\frac{2 e d}{\sqrt{1-e^{2}}}$
• If $e = 1$, the graph is a parabola whose focal diameter is $2d$.
• If $e > 1$, the graph is a hyperbola whose transverse axis has length $\frac{2 e d}{e^{2}-1}$ and whose conjugate axis has length $\frac{2 e d}{\sqrt{e^{2}-1}}$.

We test out Theorem 11.12 in the next example.

Example 11.6.4

Sketch the graphs of the following equations.

1. $r=\frac{4}{1-\sin (\theta)}$
2. $r=\frac{12}{3-\cos (\theta)}$
3. $r=\frac{6}{1+2 \sin (\theta)}$

Solution

1. From $r=\frac{4}{1-\sin (\theta)}$, we first note $e = 1$ which means we have a parabola on our hands. Since $ed = 4$, we have $d = 4$ and considering the form of the equation, this puts the directrix at $y = −4$. Since the focus is at (0, 0), we know that the vertex is located at the point (in rectangular coordinates) (0, −2) and must open upwards. With $d = 4$, we have a focal diameter of $2d = 8$, so the parabola contains the points (±4, 0). We graph $r=\frac{4}{1-\sin (\theta)}$ below.
2. We first rewrite $r=\frac{12}{3-\cos (\theta)}$ in the form found in Theorem 11.12, namely $r=\frac{4}{1-(1 / 3) \cos (\theta)}$. Since $e=\frac{1}{3}$ satisfies $0 < e < 1$, we know that the graph of this equation is an ellipse. Since $ed = 4$, we have $d = 12$ and, based on the form of the equation, the directrix is $x = −12$. This means that the ellipse has its major axis along the $x$-axis. We can find the vertices of the ellipse by finding the points of the ellipse which lie on the $x$-axis. We find $r(0) = 6$ and $r(\pi)=3$ which correspond to the rectangular points (−3, 0) and (6, 0), so these are our vertices. The center of the ellipse is the midpoint of the vertices, which in this case is $\left(\frac{3}{2}, 0\right)$.⁸ We know one focus is (0, 0), which is $\frac{3}{2}$ from the center $\left(\frac{3}{2}, 0\right)$ and this allows us to find the other focus (3, 0), even though we are not asked to do so. Finally, we know from Theorem 11.12 that the length of the minor axis is $\frac{2 e d}{\sqrt{1-e^{2}}}=\frac{4}{\sqrt{1-(1 / 3)^{2}}}=6 \sqrt{3}$ which means the endpoints of the minor axis are $\left(\frac{3}{2}, \pm 3 \sqrt{2}\right)$. We now have everything we need to graph $r=\frac{12}{3-\cos (\theta)}$.

   

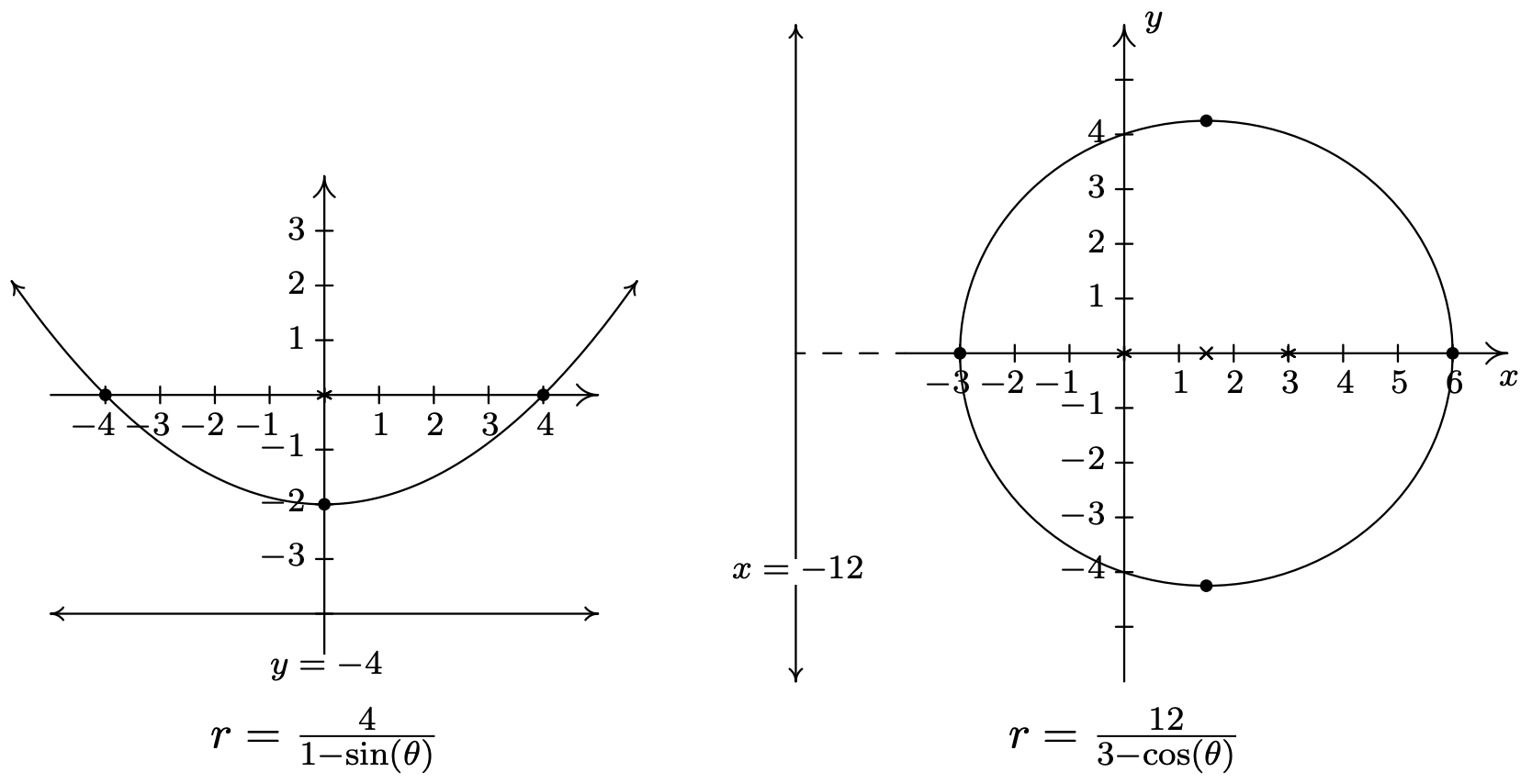
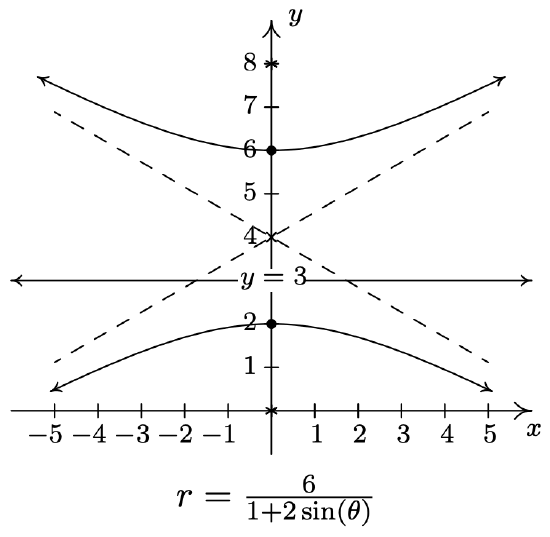
3. From $r=\frac{6}{1+2 \sin (\theta)}$ we get $e = 2 > 1$ so the graph is a hyperbola. Since $ed = 6$, we get $d = 3$, and from the form of the equation, we know the directrix is $y = 3$. This means the transverse axis of the hyperbola lies along the $y$-axis, so we can find the vertices by looking where the hyperbola intersects the $y$-axis. We find $r\left(\frac{\pi}{2}\right)=2$ and $r\left(\frac{3 \pi}{2}\right)=-6$. These two points correspond to the rectangular points (0, 2) and (0, 6) which puts the center of the hyperbola at (0, 4). Since one focus is at (0, 0), which is 4 units away from the center, we know the other focus is at (0, 8). According to Theorem 11.12, the conjugate axis has a length of $\frac{2 e d}{\sqrt{e^{2}-1}}=\frac{(2)(6)}{\sqrt{2^{2}-1}}=4 \sqrt{3}$. Putting this together with the location of the vertices, we get that the asymptotes of the hyperbola have slopes $\pm \frac{2}{2 \sqrt{3}}=\pm \frac{\sqrt{3}}{3}$. Since the center of the hyperbola is (0, 4), the asymptotes are $y=\pm \frac{\sqrt{3}}{3} x+4$. We graph the hyperbola below.

   

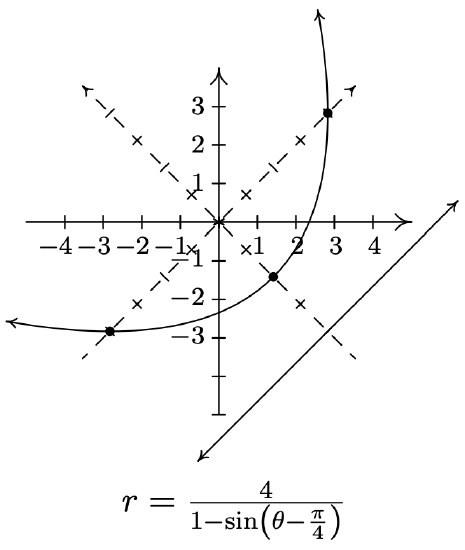
In light of Section 11.6.1, the reader may wonder what the rotated form of the conic sections would look like in polar form. We know from Exercise 65 in Section 11.5 that replacing $\theta$ with $(\theta-\phi)$ in an expression $r=f(\theta)$ rotates the graph of $r=f(\theta)$ counter-clockwise by an angle $\phi$. For instance, to graph $r=\frac{4}{1-\sin \left(\theta-\frac{\pi}{4}\right)}$ all we need to do is rotate the graph of $r=\frac{4}{1-\sin (\theta)}$, which we obtained in Example 11.6.4 number 1, counter-clockwise by $\frac{\pi}{4}$ radians, as shown below.

Using rotations, we can greatly simplify the form of the conic sections presented in Theorem 11.12, since any three of the forms given there can be obtained from the fourth by rotating through some multiple of $\frac{\pi}{2}$. Since rotations do not affect lengths, all of the formulas for lengths Theorem 11.12 remain intact. In the theorem below, we also generalize our formula for conic sections to include circles centered at the origin by extending the concept of eccentricity to include $e = 0$. We conclude this section with the statement of the following theorem.

Theorem 11.13

Given constants $\ell>0, e \geq 0$ and $\phi$, the graph of the equation

$r=\frac{\ell}{1-e \cos (\theta-\phi)}$

is a conic section with eccentricity $e$ and one focus at (0, 0).

• If $e = 0$, the graph is a circle centered at (0, 0) with radius $\ell$.
• If $e \neq 0$, then the conic has a focus at (0, 0) and the directrix contains the point with polar coordinates $(-d, \phi)$ where $d=\frac{\ell}{e}$.
  • If $0 < e < 1$, the graph is an ellipse whose major axis has length $\frac{2 e d}{1-e^{2}}$ and whose minor axis has length $\frac{2 e d}{\sqrt{1-e^{2}}}$
  • If $e = 1$, the graph is a parabola whose focal diameter is $2d$.
  • If $e > 1$, the graph is a hyperbola whose transverse axis has length $\frac{2 e d}{e^{2}-1}$ and whose conjugate axis has length $\frac{2 e d}{\sqrt{e^{2}-1}}$.

11.6.3 Exercises

Graph the following equations.

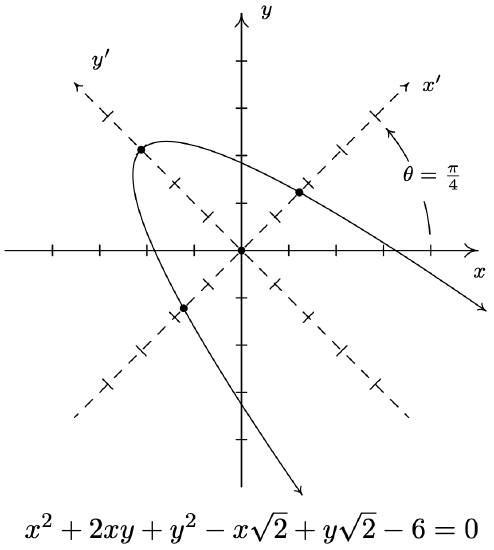
1. $x^{2}+2 x y+y^{2}-x \sqrt{2}+y \sqrt{2}-6=0$
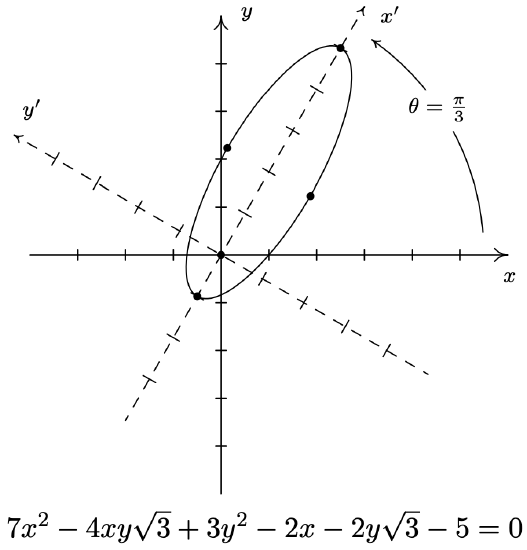
2. $7 x^{2}-4 x y \sqrt{3}+3 y^{2}-2 x-2 y \sqrt{3}-5=0$
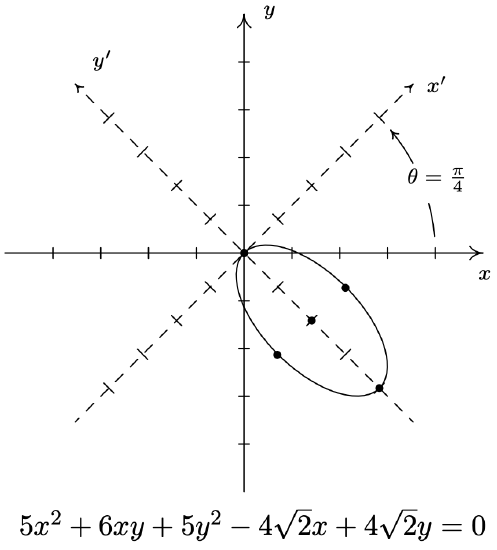
3. $5 x^{2}+6 x y+5 y^{2}-4 \sqrt{2} x+4 \sqrt{2} y=0$
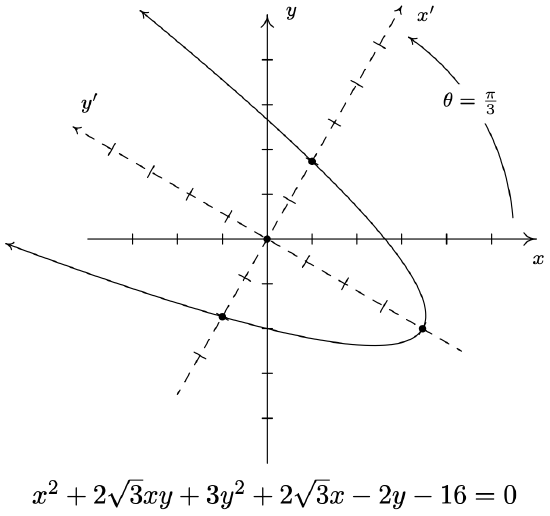
4. $x^{2}+2 \sqrt{3} x y+3 y^{2}+2 \sqrt{3} x-2 y-16=0$
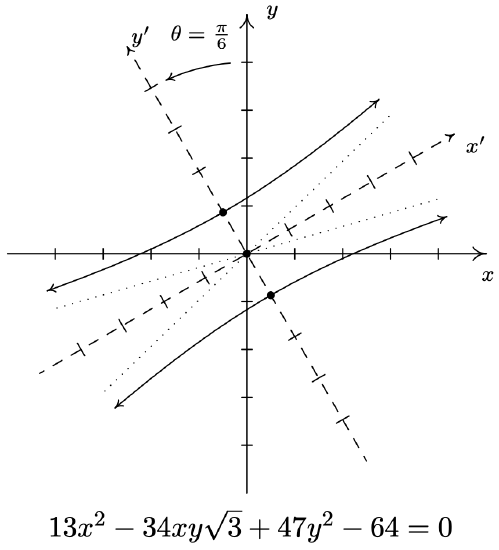
5. $13 x^{2}-34 x y \sqrt{3}+47 y^{2}-64=0$
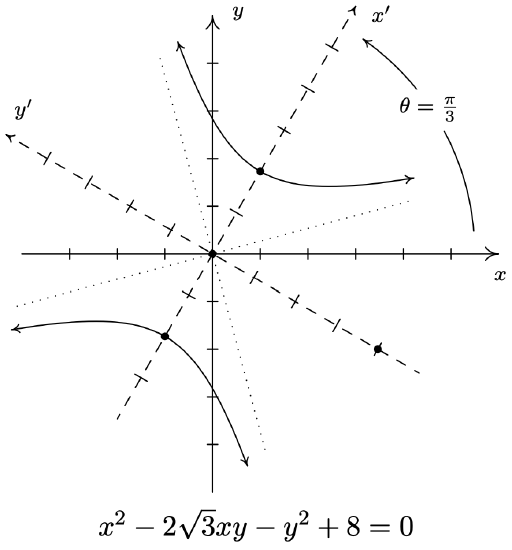
6. $x^{2}-2 \sqrt{3} x y-y^{2}+8=0$
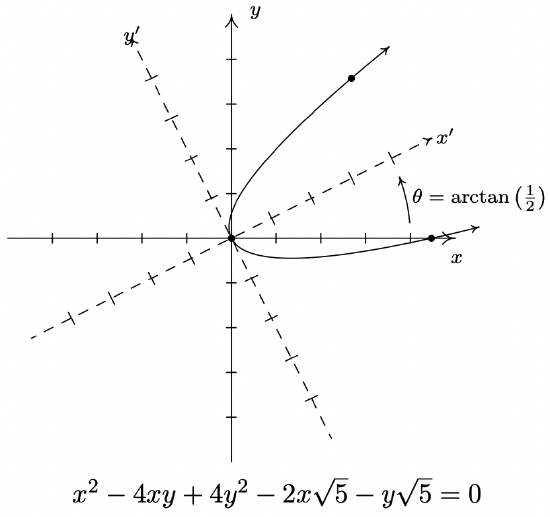
7. $x^{2}-4 x y+4 y^{2}-2 x \sqrt{5}-y \sqrt{5}=0$
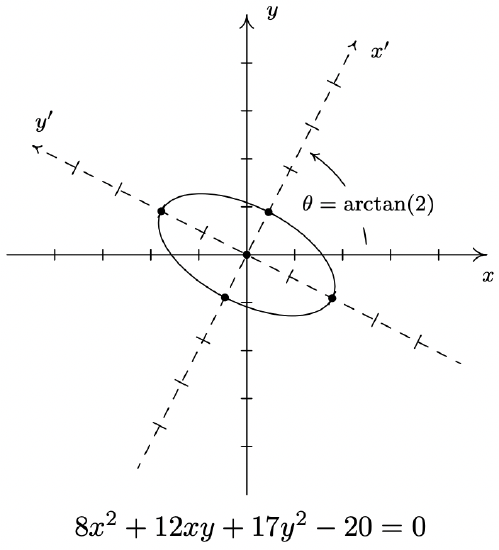
8. $8 x^{2}+12 x y+17 y^{2}-20=0$

Graph the following equations.

9. $r=\frac{2}{1-\cos (\theta)}$
10. $r=\frac{3}{2+\sin (\theta)}$
11. $r=\frac{3}{2-\cos (\theta)}$
12. $r=\frac{2}{1+\sin (\theta)}$
13. $r=\frac{4}{1+3 \cos (\theta)}$
14. $r=\frac{2}{1-2 \sin (\theta)}$
15. $r=\frac{2}{1+\sin \left(\theta-\frac{\pi}{3}\right)}$
16. $r=\frac{6}{3-\cos \left(\theta+\frac{\pi}{4}\right)}$

The matrix $A(\theta)=\left[\begin{array}{rr} \cos (\theta) & -\sin (\theta) \\ \sin (\theta) & \cos (\theta) \end{array}\right]$ is called a rotation matrix. We’ve seen this matrix most recently in the proof of used in the proof of Theorem 11.9.

17. Show the matrix from Example 8.3.3 in Section 8.3 is none other than $A\left(\frac{\pi}{4}\right)$.
18. Discuss with your classmates how to use $A(\theta)$ ) to rotate points in the plane.
19. Using the even / odd identities for cosine and sine, show $A(\theta)^{-1}=A(-\theta)$. Interpret this geometrically.

11.6.4 Answers

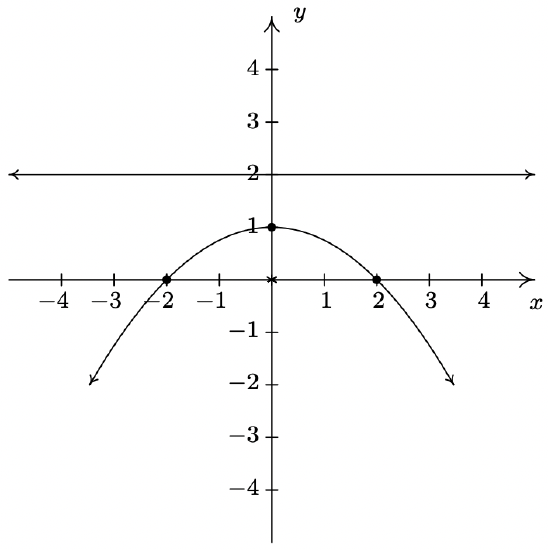
1. $x^{2}+2 x y+y^{2}-x \sqrt{2}+y \sqrt{2}-6=0$ becomes $\left(x^{\prime}\right)^{2}=-\left(y^{\prime}-3\right)$ after rotating counter-clockwise through $\theta=\frac{\pi}{4}$.

   

2. $7 x^{2}-4 x y \sqrt{3}+3 y^{2}-2 x-2 y \sqrt{3}-5=0$ becomes $\frac{\left(x^{\prime}-2\right)^{2}}{9}+\left(y^{\prime}\right)^{2}=1$ after rotating counter-clockwise through $\theta=\frac{\pi}{3}$

   

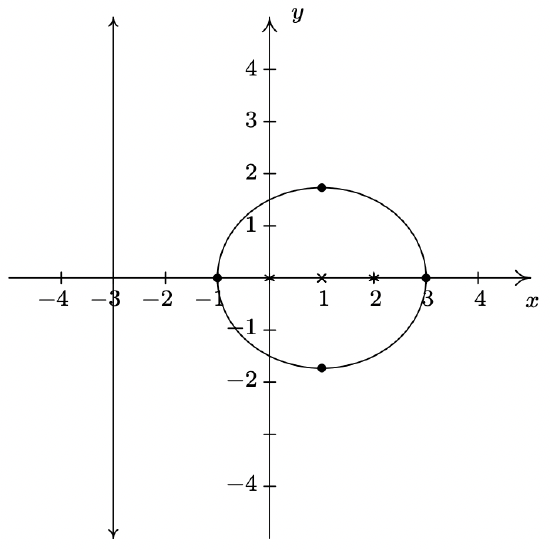
3. $5 x^{2}+6 x y+5 y^{2}-4 \sqrt{2} x+4 \sqrt{2} y=0$ becomes $\left(x^{\prime}\right)^{2}+\frac{\left(y^{\prime}+2\right)^{2}}{4}=1$ after rotating counter-clockwise through $\theta=\frac{\pi}{4}$.

   

4. $x^{2}+2 \sqrt{3} x y+3 y^{2}+2 \sqrt{3} x-2 y-16=0$ becomes $\left(x^{\prime}\right)^{2}=y^{\prime}+4$ after rotating counter-clockwise through $\theta=\frac{\pi}{3}$

   

5. $13 x^{2}-34 x y \sqrt{3}+47 y^{2}-64=0$ becomes $\left(y^{\prime}\right)^{2}-\frac{\left(x^{\prime}\right)^{2}}{16}=1$ after rotating counter-clockwise through $\theta=\frac{\pi}{6}$.

   

6. $x^{2}-2 \sqrt{3} x y-y^{2}+8=0$ becomes $\frac{\left(x^{\prime}\right)^{2}}{4}-\frac{\left(y^{\prime}\right)^{2}}{4}=1$ after rotating counter-clockwise through $\theta=\frac{\pi}{3}$

   

7. $x^{2}-4 x y+4 y^{2}-2 x \sqrt{5}-y \sqrt{5}=0$ becomes $\left(y^{\prime}\right)^{2}=x$ after rotating counter-clockwise through $\theta=\arctan \left(\frac{1}{2}\right)$.

   

8. $8 x^{2}+12 x y+17 y^{2}-20=0$ becomes $\left(x^{\prime}\right)^{2}+\frac{\left(y^{\prime}\right)^{2}}{4}=1$ after rotating counter-clockwise through $\theta=\arctan (2)$

   

9. $r=\frac{2}{1-\cos (\theta)}$ is a parabola directrix $x = −2$, vertex (−1, 0) focus (0, 0), focal diameter 4

   

10. $r=\frac{3}{2+\sin (\theta)}=\frac{\frac{3}{2}}{1+\frac{1}{2} \sin (\theta)}$ is an ellipse directrix $y = 3$, vertices (0, 1), (0, −3) center (0, −2) , foci (0, 0), (0, −2) minor axis length $2 \sqrt{3}$

    

11. $r=\frac{3}{2-\cos (\theta)}=\frac{\frac{3}{2}}{1-\frac{1}{2} \cos (\theta)}$ is an ellipse directrix $x = −3$, vertices (−1, 0), (3, 0) center (1, 0) , foci (0, 0), (2, 0) minor axis length $2 \sqrt{3}$

    

12. $r=\frac{2}{1+\sin (\theta)}$ is a parabola directrix $y = 2$, vertex (0, 1) focus (0, 0), focal diameter 4

    

13. $r=\frac{4}{1+3 \cos (\theta)}$ is a hyperbola directrix $x=\frac{4}{3}$, vertices (1, 0), (2, 0) center $\left(\frac{3}{2}, 0\right)$, foci (0, 0), (3, 0) conjugate axis length $2 \sqrt{2}$

    

14. $r=\frac{2}{1-2 \sin (\theta)}$ is a hyperbola directrix $y = −1$, vertices $\left(0,-\frac{2}{3}\right),(0,-2)$ center $\left(0,-\frac{4}{3}\right)$, foci $(0,0),\left(0,-\frac{8}{3}\right)$ conjugate axis length $\frac{2 \sqrt{3}}{3}$

    

15. $r=\frac{2}{1+\sin \left(\theta-\frac{\pi}{3}\right)}$ is the parabola $r=\frac{2}{1+\sin (\theta)}$ rotated through $\phi=\frac{\pi}{3}$

    

16. $r=\frac{6}{3-\cos \left(\theta+\frac{\pi}{4}\right)}$ is the ellipse $r=\frac{6}{3-\cos (\theta)}=\frac{2}{1-\frac{1}{3} \cos (\theta)}$ rotated through $\phi=-\frac{\pi}{4}$

    

---

Reference

¹ Sound familiar? In Section 11.4, the equations $x=r \cos (\theta)$ and $y=r \sin (\theta)$ make it easy to convert points from polar coordinates into rectangular coordinates, and they make it easy to convert equations from rectangular coordinates into polar coordinates.

² We could, of course, interchange the roles of $x$ and $x^{\prime}$, $y$ and $y^{\prime}$ and replace $\phi$ with $-\phi$ to get $x^{\prime}$ and $y^{\prime}$ in terms of $x$ and $y$, but that seems like cheating. The matrix A introduced here is revisited in the Exercises.

³ The reader is invited to think about the case $\sin (2 \theta)=0$ geometrically. What happens to the axes in this case?

⁴ As usual, there are infinitely many solutions to $\tan (\theta)=\frac{3}{4}$. We choose the acute angle $\theta=\arctan \left(\frac{3}{4}\right)$. The reader is encouraged to think about why there is always at least one acute answer to $\cot (2 \theta)=\frac{A-C}{B}$ and what this means geometrically in terms of what we are trying to accomplish by rotating the axes. The reader is also encouraged to keep a sharp lookout for the angles which satisfy $\tan (\theta)=-\frac{4}{3}$ in our final graph. (Hint: $\left(\frac{3}{4}\right)\left(-\frac{4}{3}\right)=-1$.)

⁵ We hope that someday you get to see why this works the way it does.

⁶ Turn $r=e(d+r \cos (\theta))$ into $r=e(d+x)$ and square both sides to get $r^{2}=e^{2}(d+x)^{2}$. Replace $r^2$ with $x^{2}+y^{2}$, expand $(d+x)^{2}$, combine like terms, complete the square on $x$ and clean things up.

⁷ Since, $e > 1$ in this case, $1-e^{2}<0$. Hence, we rewrite $\left(1-e^{2}\right)^{2}=\left(e^{2}-1\right)^{2}$ to help simplify things later on.

⁸ As a quick check, we have from Theorem 11.12 the major axis should have length $\frac{2 e d}{1-e^{2}}=\frac{(2)(4)}{1-(1 / 3)^{2}}=9$.