7.4: Ellipses

In the definition of a circle, Definition 7.1, we fixed a point called the center and considered all of the points which were a fixed distance \(r\) from that one point. For our next conic section, the ellipse, we fix two distinct points and a distance \(d\) to use in our definition.

Definition 7.4

Given two distinct points \(F_{1}\) and \(F_{2}\) in the plane and a fixed distance \(d\), an ellipse is the set of all points \((x, y)\) in the plane such that the sum of each of the distances from \(F_{1}\) and \(F_{2}\) to \((x, y)\) is \(d\). The points \(F_{1}\) and \(F_{2}\) are called the foci^a of the ellipse.

---

^a the plural of ‘focus’

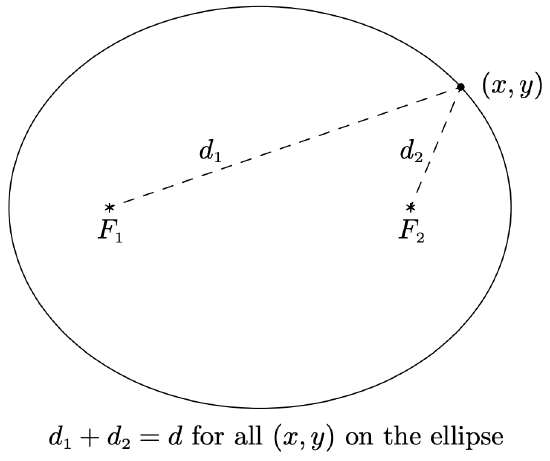
We may imagine taking a length of string and anchoring it to two points on a piece of paper. The curve traced out by taking a pencil and moving it so the string is always taut is an ellipse.

The center of the ellipse is the midpoint of the line segment connecting the two foci. The major axis of the ellipse is the line segment connecting two opposite ends of the ellipse which also contains the center and foci. The minor axis of the ellipse is the line segment connecting two opposite ends of the ellipse which contains the center but is perpendicular to the major axis. The vertices of an ellipse are the points of the ellipse which lie on the major axis. Notice that the center is also the midpoint of the major axis, hence it is the midpoint of the vertices. In pictures we have,

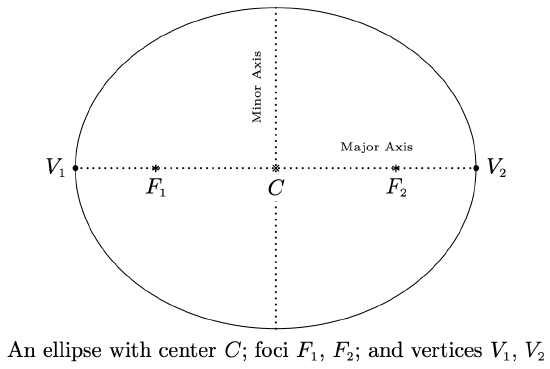
Note that the major axis is the longer of the two axes through the center, and likewise, the minor axis is the shorter of the two. In order to derive the standard equation of an ellipse, we assume that the ellipse has its center at \((0,0)\), its major axis along the \(x\)-axis, and has foci \((c,0)\) and \((-c,0)\) and vertices \((-a,0)\) and \((a,0)\). We will label the \(y\)-intercepts of the ellipse as \((0,b)\) and \((0,-b)\) (We assume \(a\), \(b\), and \(c\) are all positive numbers.) Schematically,

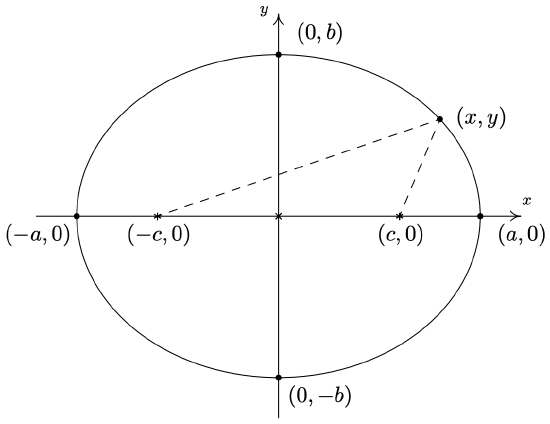
Note that since \((a,0)\) is on the ellipse, it must satisfy the conditions of Definition 7.4. That is, the distance from \((-c,0)\) to \((a,0)\) plus the distance from \((c,0)\) to \((a,0)\) must equal the fixed distance \(d\). Since all of these points lie on the \(x\)-axis, we get

\[\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(a,0)$} + \mbox{distance from $(c,0)$ to $(a,0)$} & = & d & \\ (a+c) + (a-c) & = & d & \\ 2a & = & d \\ \end{array}\nonumber\]

In other words, the fixed distance \(d\) mentioned in the definition of the ellipse is none other than the length of the major axis. We now use that fact \((0,b)\) is on the ellipse, along with the fact that \(d=2a\) to get

\[\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(0,b)$} + \mbox{distance from $(c,0)$ to $(0,b)$} & = & 2a & \\ \sqrt{(0-(-c))^2+(b-0)^2} + \sqrt{(0-c)^2+(b-0)^2} & = & 2a & \\ \sqrt{b^2+c^2}+\sqrt{b^2+c^2} & = & 2a \\ 2 \sqrt{b^2+c^2} & = & 2a \\ \sqrt{b^2+c^2} & = & a \end{array}\nonumber\]

From this, we get \(a^2 = b^2 + c^2\), or \(b^2 = a^2 - c^2\), which will prove useful later. Now consider a point \((x,y)\) on the ellipse. Applying Definition 7.4, we get

\[\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(x,y)$} + \mbox{distance from $(c,0)$ to $(x,y)$} & = & 2a & \\ \sqrt{(x-(-c))^2+(y-0)^2} + \sqrt{(x-c)^2+(y-0)^2} & = & 2a & \\ \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} & = & 2a \\ \end{array}\nonumber\]

In order to make sense of this situation, we need to make good use of Intermediate Algebra.

\[\begin{array}{rclr} \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} & = & 2a & \\ \sqrt{(x+c)^2+y^2} & = & 2a - \sqrt{(x-c)^2+y^2} & \\ \left(\sqrt{(x+c)^2+y^2}\right)^2 & = & \left(2a - \sqrt{(x-c)^2+y^2}\right)^2 & \\ (x+c)^2+y^2 & = & 4a^2 - 4a\sqrt{(x-c)^2+y^2} + (x-c)^2+y^2 & \\ 4a\sqrt{(x-c)^2+y^2} & = & 4a^2 + (x-c)^2 - (x+c)^2 & \\ 4a\sqrt{(x-c)^2+y^2} & = & 4a^2 - 4cx & \\ a\sqrt{(x-c)^2+y^2} & = & a^2 - cx & \\ \left(a\sqrt{(x-c)^2+y^2}\right)^2 & = & \left(a^2 - cx\right)^2 & \\ a^2\left((x-c)^2+y^2\right) & = & a^4 - 2a^2cx +c^2 x^2 & \\ a^2x^2 - 2a^2cx + a^2c^2+a^2 y^2 & = & a^4 - 2a^2cx +c^2 x^2 & \\ a^2x^2 - c^2 x^2 +a^2 y^2 & = & a^4 - a^2c^2 & \\ \left(a^2 - c^2\right) x^2 +a^2 y^2 & = & a^2 \left(a^2 - c^2\right) & \\ \end{array}\nonumber\]

We are nearly finished. Recall that \(b^2 = a^2 - c^2\) so that

\[\begin{array}{rclr} \left(a^2 - c^2\right)x^2 +a^2 y^2 & = & a^2\left(a^2 - c^2\right) & \\ b^2 x^2 +a^2 y^2 & = & a^2 b^2 & \\ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} & = & 1 & \\ \end{array}\nonumber\]

This equation is for an ellipse centered at the origin. To get the formula for the ellipse centered at \((h,k)\), we could use the transformations from Section 1.7 or re-derive the equation using Definition 7.4 and the distance formula to obtain the formula below.

Equation 7.4. The Standard Equation of an Ellipse

The Standard Equation of an Ellipse: For positive unequal numbers \(a\) and \(b\), the equation of an ellipse with center \((h,k)\) is

\[\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1\nonumber\]

Some remarks about Equation 7.4 are in order. First note that the values \(a\) and \(b\) determine how far in the \(x\) and \(y\) directions, respectively, one counts from the center to arrive at points on the ellipse. Also take note that if \(a > b\), then we have an ellipse whose major axis is horizontal, and hence, the foci lie to the left and right of the center. In this case, as we’ve seen in the derivation, the distance from the center to the focus, \(c\), can be found by \(c = \sqrt{a^2 - b^2}\). If \(b > a\), the roles of the major and minor axes are reversed, and the foci lie above and below the center. In this case, \(c = \sqrt{b^2 - a^2}\). In either case, \(c\) is the distance from the center to each focus, and \(c = \sqrt{\mbox{bigger denominator} - \mbox{smaller denominator}}\). Finally, it is worth mentioning that if we take the standard equation of a circle, Equation 7.1, and divide both sides by \(r^2\), we get

Equation 7.5. The Alternate Standard Equation of a Circle

The Alternate Standard Equation of a Circle: The equation of a circle with center \((h,k)\) and radius \(r >0\) is

\[\dfrac{(x-h)^2}{r^2} + \dfrac{(y-k)^2}{r^2} = 1\nonumber\]

Notice the similarity between Equation 7.4 and Equation 7.5. Both equations involve a sum of squares equal to \(1\); the difference is that with a circle, the denominators are the same, and with an ellipse, they are different. If we take a transformational approach, we can consider both Equations 7.4 and 7.5 as shifts and stretches of the Unit Circle \(x^2 + y^2 = 1\) in Definition 7.2. Replacing \(x\) with \((x-h)\) and \(y\) with \((y-k)\) causes the usual horizontal and vertical shifts. Replacing \(x\) with \(\frac{x}{a}\) and \(y\) with \(\frac{y}{b}\) causes the usual vertical and horizontal stretches. In other words, it is perfectly fine to think of an ellipse as the deformation of a circle in which the circle is stretched farther in one direction than the other.¹

Example 7.4.1

Graph \(\frac{(x+1)^2}{9} + \frac{(y-2)^2}{25} = 1\). Find the center, the lines which contain the major and minor axes, the vertices, the endpoints of the minor axis, and the foci.

Solution

We see that this equation is in the standard form of Equation 7.4. Here \(x-h\) is \(x+1\) so \(h = -1\), and \(y-k\) is \(y-2\) so \(k = 2\). Hence, our ellipse is centered at \((-1,2)\). We see that \(a^2 = 9\) so \(a=3\), and \(b^2 = 25\) so \(b=5\). This means that we move \(3\) units left and right from the center and \(5\) units up and down from the center to arrive at points on the ellipse. As an aid to sketching, we draw a rectangle matching this description, called a guide rectangle, and sketch the ellipse inside this rectangle as seen below on the left.

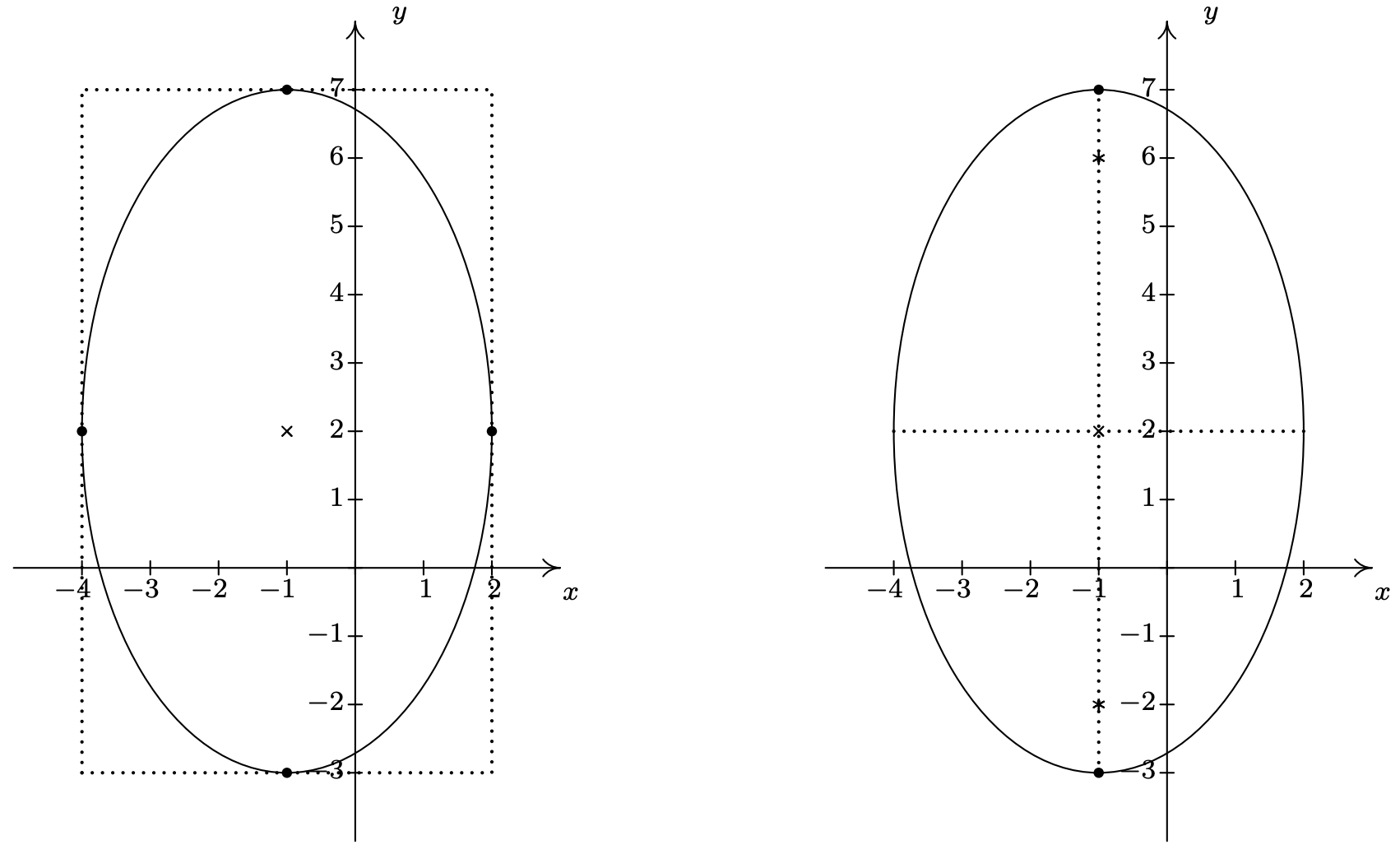
Since we moved farther in the \(y\) direction than in the \(x\) direction, the major axis will lie along the vertical line \(x=-1\), which means the minor axis lies along the horizontal line, \(y = 2\). The vertices are the points on the ellipse which lie along the major axis so in this case, they are the points \((-1,7)\) and \((-1,-3)\), and the endpoints of the minor axis are \((-4,2)\) and \((2,2)\). (Notice these points are the four points we used to draw the guide rectangle.) To find the foci, we find \(c = \sqrt{25-9} = \sqrt{16} = 4\), which means the foci lie \(4\) units from the center. Since the major axis is vertical, the foci lie \(4\) units above and below the center, at \((-1,-2)\) and \((-1,6)\). Plotting all this information gives the graph seen above on the right.

Example 7.4.2

Find the equation of the ellipse with foci \((2,1)\) and \((4,1)\) and vertex \((0,1)\).

Solution

Plotting the data given to us, we have

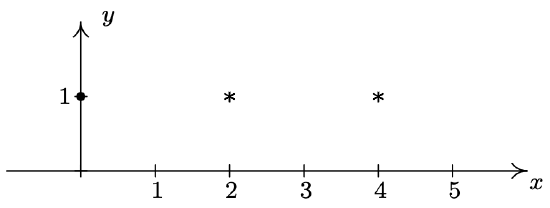
From this sketch, we know that the major axis is horizontal, meaning \(a > b\). Since the center is the midpoint of the foci, we know it is \((3, 1)\). Since one vertex is \((0,1)\) we have that \(a = 3\), so \(a^2 = 9\). All that remains is to find \(b^2\). Since the foci are \(1\) unit away from the center, we know \(c=1\). Since \(a > b\), we have \(c = \sqrt{a^2-b^2}\), or \(1 = \sqrt{9-b^2}\), so \(b^2 = 8\). Substituting all of our findings into the equation \(\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1\), we get our final answer to be \(\frac{(x-3)^2}{9}+\frac{(y-1)^2}{8}=1\).

As with circles and parabolas, an equation may be given which is an ellipse, but isn’t in the standard form of Equation 7.4. In those cases, as with circles and parabolas before, we will need to massage the given equation into the standard form.

To Write the Equation of an Ellipse in Standard Form

1. Group the same variables together on one side of the equation and position the constant on the other side.
2. Complete the square in both variables as needed.
3. Divide both sides by the constant term so that the constant on the other side of the equation becomes \(1\).

Example 7.4.3

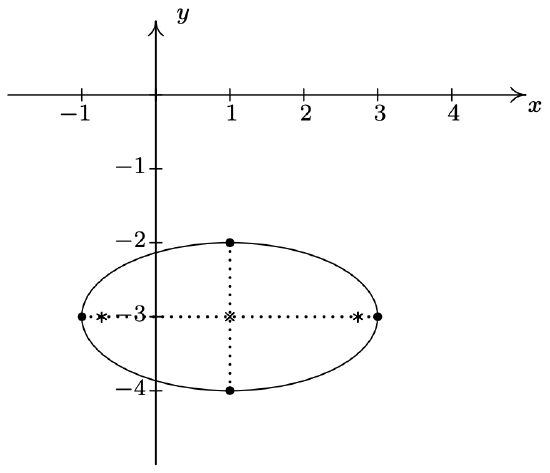
Graph \(x^2+4y^2-2x+24y+33 = 0\). Find the center, the lines which contain the major and minor axes, the vertices, the endpoints of the minor axis, and the foci.

Solution

Since we have a sum of squares and the squared terms have unequal coefficients, it’s a good bet we have an ellipse on our hands.² We need to complete both squares, and then divide, if necessary, to get the right-hand side equal to \(1\).

\[\begin{array}{rclr} x^2+4y^2-2x+24y+33 & = & 0 & \\ x^2-2x+4y^2+24y & = & -33 & \\ x^2 - 2x + 4\left(y^2+6y\right) & = & - 33 & \\ \left(x^2 - 2x +1\right) + 4\left(y^2+6y+9\right) & = & - 33 + 1 + 4(9)& \\ (x-1)^2 + 4(y+3)^2 & = & 4 & \\[5pt] \dfrac{(x-1)^2 + 4(y+3)^2}{4} & = & \dfrac{4}{4} & \\[10pt] \dfrac{(x-1)^2}{4} + (y+3)^2 & = & 1 & \\[10pt] \dfrac{(x-1)^2}{4} + \dfrac{(y+3)^2}{1} & = & 1 & \\ \end{array}\nonumber\]

Now that this equation is in the standard form of Equation 7.4, we see that \(x-h\) is \(x-1\) so \(h = 1\), and \(y-k\) is \(y+3\) so \(k = -3\). Hence, our ellipse is centered at \((1,-3)\). We see that \(a^2 = 4\) so \(a=2\), and \(b^2 = 1\) so \(b=1\). This means we move \(2\) units left and right from the center and \(1\) unit up and down from the center to arrive at points on the ellipse. Since we moved farther in the \(x\) direction than in the \(y\) direction, the major axis will lie along the horizontal line \(y=-3\), which means the minor axis lies along the vertical line \(x = 1\). The vertices are the points on the ellipse which lie along the major axis so in this case, they are the points \((-1,-3)\) and \((3,-3)\), and the endpoints of the minor axis are \((1,-2)\) and \((1,-4)\). To find the foci, we find \(c = \sqrt{4-1} = \sqrt{3}\), which means the foci lie \(\sqrt{3}\) units from the center. Since the major axis is horizontal, the foci lie \(\sqrt{3}\) units to the left and right of the center, at \((1-\sqrt{3},-3)\) and \((1+\sqrt{3},-3)\). Plotting all of this information gives

As you come across ellipses in the homework exercises and in the wild, you’ll notice they come in all shapes in sizes. Compare the two ellipses below.

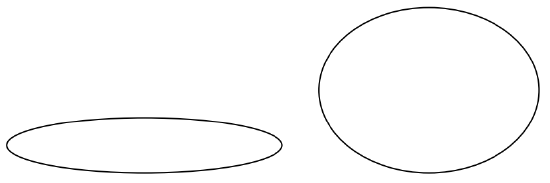
Certainly, one ellipse is more round than the other. This notion of ‘roundness’ is quantified below.

Definition 7.5

The eccentricity of an ellipse, denoted \(e\), is the following ratio:

\[e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}}\nonumber\]

In an ellipse, the foci are closer to the center than the vertices, so \(0 < e < 1\). The ellipse above on the left has eccentricity \(e \approx 0.98\); for the ellipse above on the right, \(e \approx 0.66\). In general, the closer the eccentricity is to \(0\), the more ‘circular’ the ellipse; the closer the eccentricity is to \(1\), the more ‘eccentric’ the ellipse.

Example 7.4.4

Find the equation of the ellipse whose vertices are \((\pm 5,0 )\) with eccentricity \(e = \frac{1}{4}\).

Solution

As before, we plot the data given to us

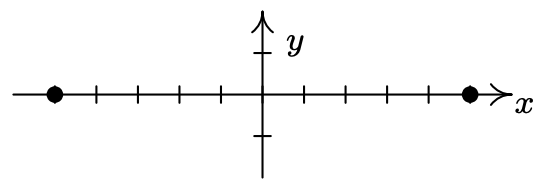
From this sketch, we know that the major axis is horizontal, meaning \(a > b\). With the vertices located at \((\pm 5,0)\), we get \(a = 5\) so \(a^2 = 25\). We also know that the center is \((0,0)\) because the center is the midpoint of the vertices. All that remains is to find \(b^2\). To that end, we use the fact that the eccentricity \(e = \frac{1}{4}\) which means

\[e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}} = \dfrac{c}{a} = \dfrac{c}{5} = \dfrac{1}{4}\nonumber\]

from which we get \(c = \frac{5}{4}\). To get \(b^2\), we use the fact that \(c = \sqrt{a^2 - b^2}\), so \(\frac{5}{4} = \sqrt{25-b^2}\) from which we get \(b^2 = \frac{375}{16}\). Substituting all of our findings into the equation \(\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1\), yields our final answer \(\frac{x^2}{25} + \frac{16y^2}{375}=1\).

As with parabolas, ellipses have a reflective property. If we imagine the dashed lines below representing sound waves, then the waves emanating from one focus reflect off the top of the ellipse and head towards the other focus.

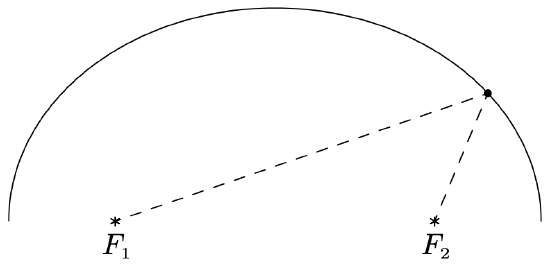
Such geometry is exploited in the construction of so-called ‘Whispering Galleries’. If a person whispers at one focus, a person standing at the other focus will hear the first person as if they were standing right next to them. We explore the Whispering Galleries in our last example.

Example 7.4.5

Jamie and Jason want to exchange secrets (terrible secrets) from across a crowded whispering gallery. Recall that a whispering gallery is a room which, in cross section, is half of an ellipse. If the room is 40 feet high at the center and 100 feet wide at the floor, how far from the outer wall should each of them stand so that they will be positioned at the foci of the ellipse?

Solution

Graphing the data yields

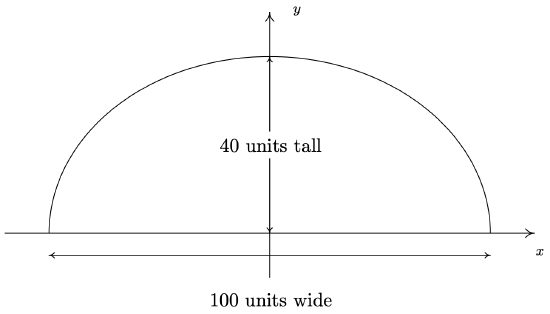
It’s most convenient to imagine this ellipse centered at \((0,0)\). Since the ellipse is \(100\) units wide and \(40\) units tall, we get \(a=50\) and \(b=40\). Hence, our ellipse has the equation \(\frac{x^2}{50^2}+\frac{y^2}{40^2} = 1\). We’re looking for the foci, and we get \(c = \sqrt{50^2-40^2} = \sqrt{900} = 30\), so that the foci are \(30\) units from the center. That means they are \(50-30=20\) units from the vertices. Hence, Jason and Jamie should stand \(20\) feet from opposite ends of the gallery.

7.4.1. Exercises

In Exercises 1 - 8, graph the ellipse. Find the center, the lines which contain the major and minor axes, the vertices, the endpoints of the minor axis, the foci and the eccentricity.

1. \(\dfrac{x^{2}}{169} + \dfrac{y^{2}}{25} = 1\)
2. \(\dfrac{x^2}{9} + \dfrac{y^2}{25} = 1\)
3. \(\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1\)
4. \(\dfrac{(x + 5)^{2}}{16} + \dfrac{(y - 4)^{2}}{1} = 1\)
5. \(\dfrac{(x - 1)^{2}}{10} + \dfrac{(y - 3)^{2}}{11} = 1\)
6. \(\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1\)
7. \(\dfrac{(x+2)^2}{16}+\dfrac{(y-5)^2}{20} = 1\)
8. \(\dfrac{(x-4)^2}{8} + \dfrac{(y-2)^2}{18} = 1\)

In Exercises 9 - 14, put the equation in standard form. Find the center, the lines which contain the major and minor axes, the vertices, the endpoints of the minor axis, the foci and the eccentricity.

9. \(9x^2+25y^2-54x-50y-119=0\)
10. \(12x^{2} + 3y^{2} - 30y + 39 = 0\)
11. \(5x^{2} + 18y^{2} - 30x + 72y + 27 = 0\)
12. \(x^2 - 2x + 2y^2 - 12y + 3 = 0\)
13. \(9x^2 + 4y^2 - 4y - 8 = 0\)
14. \(6x^2+5y^2-24x+20y+14=0\)

In Exercises 15 - 20, find the standard form of the equation of the ellipse which has the given properties.

15. Center \((3, 7)\), Vertex \((3, 2)\), Focus \((3, 3)\)
16. Foci \((0, \pm 5)\), Vertices \((0, \pm 8)\).
17. Foci \((\pm 3, 0)\), length of the Minor Axis \(10\)
18. Vertices \((3,2)\), \((13,2)\); Endpoints of the Minor Axis \((8,4)\), \((8,0)\)
19. Center \((5,2)\), Vertex \((0,2)\), eccentricity \(\frac{1}{2}\)
20. All points on the ellipse are in Quadrant IV except \((0, -9)\) and \((8, 0)\). (One might also say that the ellipse is “tangent to the axes” at those two points.)
21. Repeat Example 7.4.5 for a whispering gallery 200 feet wide and 75 feet tall.
22. An elliptical arch is constructed which is 6 feet wide at the base and 9 feet tall in the middle. Find the height of the arch exactly 1 foot in from the base of the arch. Compare your result with your answer to Exercise 21 in Section 7.3.
23. The Earth’s orbit around the sun is an ellipse with the sun at one focus and eccentricity \(e \approx 0.0167\). The length of the semimajor axis (that is, half of the major axis) is defined to be \(1\) astronomical unit (AU). The vertices of the elliptical orbit are given special names: ‘aphelion’ is the vertex farthest from the sun, and ‘perihelion’ is the vertex closest to the sun. Find the distance in AU between the sun and aphelion and the distance in AU between the sun and perihelion.
24. The graph of an ellipse clearly fails the Vertical Line Test, Theorem 1.1, so the equation of an ellipse does not define \(y\) as a function of \(x\). However, much like with circles and horizontal parabolas, we can split an ellipse into a top half and a bottom half, each of which would indeed represent \(y\) as a function of \(x\). With the help of your classmates, use your calculator to graph the ellipses given in Exercises 1 - 8 above. What difficulties arise when you plot them on the calculator?
25. Some famous examples of whispering galleries include St. Paul’s Cathedral in London, England, National Statuary Hall in Washington, D.C., and The Cincinnati Museum Center. With the help of your classmates, research these whispering galleries. How does the whispering effect compare and contrast with the scenario in Example Example 7.4.5?
26. With the help of your classmates, research “extracorporeal shock-wave lithotripsy”. It uses the reflective property of the ellipsoid to dissolve kidney stones.

Answers

1. \(\dfrac{x^{2}}{169} + \dfrac{y^{2}}{25} = 1\)

   Center \((0, 0)\)
   Major axis along \(y = 0\)
   Minor axis along \(x = 0\)
   Vertices \((13, 0), \, (-13, 0)\)
   Endpoints of Minor Axis \((0,-5)\), \((0,5)\)
   Foci \((12, 0), \, (-12, 0)\)
   \(e = \frac{12}{13}\)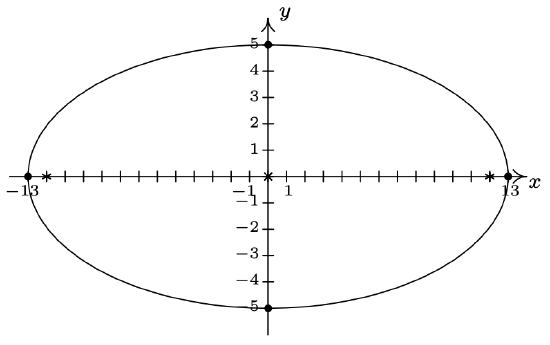

   

2. \(\dfrac{x^{2}}{9} + \dfrac{y^{2}}{25} = 1\)

   Center \((0, 0)\)
   Major axis along \(x = 0\)
   Minor axis along \(y = 0\)
   Vertices \((0,5), \, (0,-5)\)
   Endpoints of Minor Axis \((-3,0)\), \((3,0)\)
   Foci \((0,-4), \, (0,4)\)
   \(e = \frac{4}{5}\)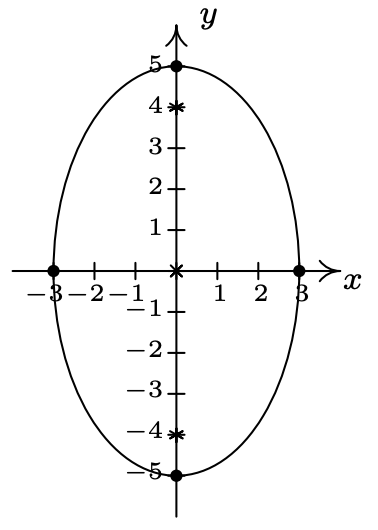

   

3. \(\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1\)

   Center \((2, -3)\)
   Major axis along \(x = 2\)
   Minor axis along \(y = -3\)
   Vertices \((2, 0), \, (2, -6)\)
   Endpoints of Minor Axis \((0,-3)\), \((4,-3)\)
   Foci \((2, -3 + \sqrt{5}), \, (2, -3 - \sqrt{5})\)
   \(e = \frac{\sqrt{5}}{3}\)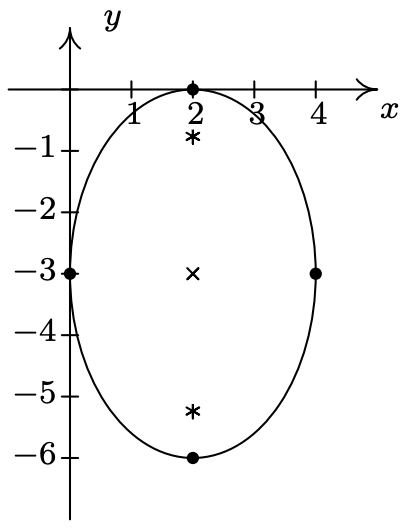

   

4. \(\dfrac{(x + 5)^{2}}{16} + \dfrac{(y - 4)^{2}}{1} = 1\)

   Center \((-5, 4)\)
   Major axis along \(y = 4\)
   Minor axis along \(x = -5\)
   Vertices \((-9, 4), \, (-1, 4)\)
   Endpoints of Minor Axis \((-5,3)\), \((-5,5)\)
   Foci \((-5 + \sqrt{15}, 4), \, (-5 - \sqrt{15}, 4)\)
   \(e = \frac{\sqrt{15}}{4}\)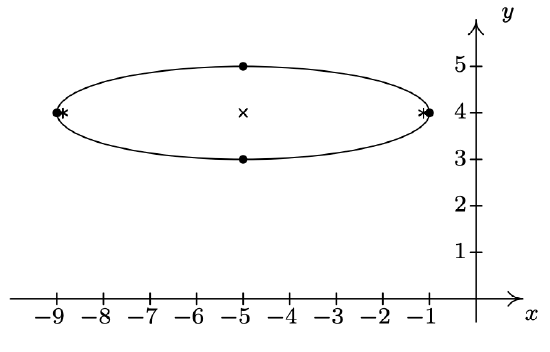

   

5. \(\dfrac{(x - 1)^{2}}{10} + \dfrac{(y - 3)^{2}}{11} = 1\)

   Center \((1, 3)\)
   Major axis along \(x = 1\)
   Minor axis along \(y = 3\)
   Vertices \((1, 3 + \sqrt{11}), \, (1, 3 - \sqrt{11})\)
   Endpoints of the Minor Axis
   \((1-\sqrt{10}, 3), \, (1+\sqrt{10}, 3)\)
   Foci \((1, 2), \, (1, 4)\)
   \(e = \frac{\sqrt{11}}{11}\)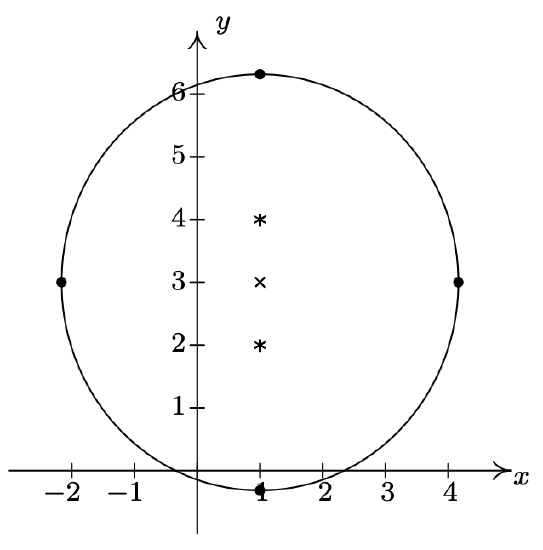

   

6. \(\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1\)

   Center \((1, -3)\)
   Major axis along \(y = -3\)
   Minor axis along \(x = 1\)
   Vertices \((4, -3), \, (-2, -3)\)
   Endpoints of the Minor Axis \((1,-1)\), \((1,-5)\)
   Foci \((1+\sqrt{5}, -3), \, (1-\sqrt{5}, -3)\)
   \(e = \frac{\sqrt{5}}{3}\)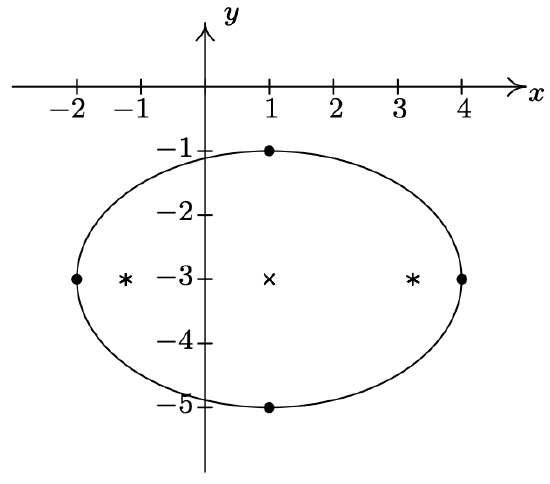

   

7. \(\dfrac{(x+2)^2}{16}+\dfrac{(y-5)^2}{20} = 1\)

   Center \((-2, 5)\)
   Major axis along \(x = -2\)
   Minor axis along \(y = 5\)
   Vertices \((-2, 5 + 2\sqrt{5}), \, (-2, 5 - 2\sqrt{5})\)
   Endpoints of the Minor Axis \((-6,5)\), \((2,5)\) Foci \((-2, 7), \, (-2, 3)\)
   \(e = \frac{\sqrt{5}}{5}\)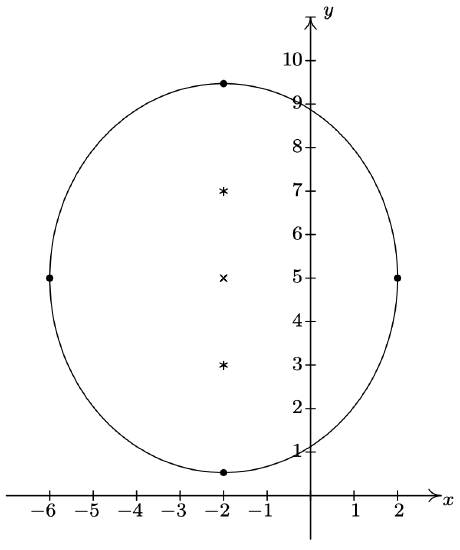

   

8. \(\dfrac{(x-4)^2}{8}+\dfrac{(y-2)^2}{18} = 1\)

   Center \((4, 2)\)
   Major axis along \(x = 4\)
   Minor axis along \(y = 2\)
   Vertices \((4, 2 + 3\sqrt{2}), \, (4, 2 - 3\sqrt{2})\)
   Endpoints of the Minor Axis
   \((4-2\sqrt{2},2)\), \((4+2\sqrt{2},2)\)
   Foci \((4, 2+\sqrt{10}), \, (4, 2-\sqrt{10})\)
   \(e = \frac{\sqrt{5}}{3}\)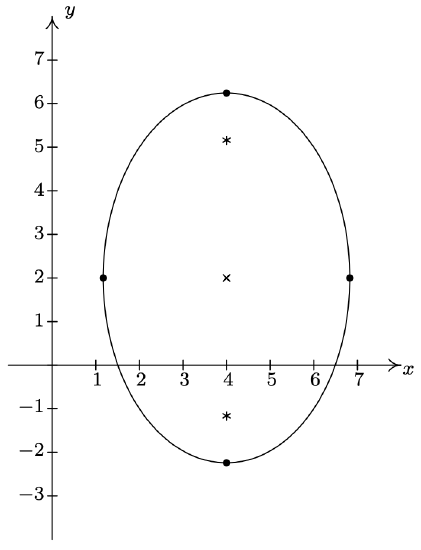

   

9. \(\dfrac{(x-3)^2}{25} + \dfrac{\left(y-1\right)^2}{9} = 1\)
   Center \(\left(3, 1 \right)\)
   Major Axis along \(y=1\)
   Minor Axis along \(x=3\)
   Vertices \(\left( 8, 1 \right)\), \((-2, 1)\)
   Endpoints of Minor Axis \(\left(3,4\right)\), \(\left(3,-2\right)\)
   Foci \(\left(7,1 \right)\), \(\left(-1, 1\right)\)
   \(e = \frac{4}{5}\)

10. \(\dfrac{x^{2}}{3} + \dfrac{(y - 5)^{2}}{12} = 1\)
    Center \((0, 5)\)
    Major axis along \(x = 0\)
    Minor axis along \(y = 5\)
    Vertices \((0, 5 - 2\sqrt{3}), (0, 5 + 2\sqrt{3})\)
    Endpoints of Minor Axis \((-\sqrt{3},5)\), \((\sqrt{3},5)\)
    Foci \((0, 2), (0, 8)\)
    \(e = \frac{\sqrt{3}}{2}\)

11. \(\dfrac{(x - 3)^{2}}{18} + \dfrac{(y + 2)^{2}}{5} = 1\)
    Center \((3, -2)\)
    Major axis along \(y = -2\)
    Minor axis along \(x = 3\)
    Vertices \((3 - 3\sqrt{2}, -2), (3 + 3\sqrt{2}, -2)\)
    Endpoints of Minor Axis \((3,-2+\sqrt{5})\), \((3,-2-\sqrt{5})\)
    Foci \((3 - \sqrt{13}, -2), (3 + \sqrt{13}, -2)\)
    \(e = \frac{\sqrt{26}}{6}\)

12. \(\dfrac{(x - 1)^{2}}{16} + \dfrac{(y - 3)^{2}}{8} = 1\)
    Center \((1,3)\)
    Major Axis along \(y=3\)
    Minor Axis along \(x=1\)
    Vertices \((5, 3)\), \((-3,3)\)
    Endpoints of Minor Axis \((1,3+2\sqrt{2})\), \((1,3-2\sqrt{2})\)
    Foci \((1 + 2 \sqrt{2}, 3)\), \((1-2 \sqrt{2},3)\)
    \(e = \frac{\sqrt{2}}{2}\)

13. \(\dfrac{x^2}{1} + \dfrac{4\left(y-\frac{1}{2}\right)^2}{9} = 1\)
    Center \(\left(0, \frac{1}{2} \right)\)
    Major Axis along \(x=0\) (the \(y\)-axis)
    Minor Axis along \(y=\frac{1}{2}\)
    Vertices \(\left( 0, 2 \right)\), \((0, -1)\)
    Endpoints of Minor Axis \(\left(-1, \frac{1}{2} \right)\), \(\left(1, \frac{1}{2} \right)\)
    Foci \(\left(0, \frac{1+\sqrt{5}}{2}\right)\), \(\left(0, \frac{1-\sqrt{5}}{2}\right)\)
    \(e = \frac{\sqrt{5}}{3}\)

14. \(\dfrac{(x-2)^2}{5} + \dfrac{\left(y+2\right)^2}{6} = 1\)
    Center \(\left(2, -2 \right)\)
    Major Axis along \(x=2\)
    Minor Axis along \(y=-2\)
    Vertices \(\left( 2, -2+\sqrt{6} \right)\), \((2, -2-\sqrt{6})\)
    Endpoints of Minor Axis \(\left(2-\sqrt{5},-2 \right)\), \(\left(2+\sqrt{5},-2\right)\)
    Foci \(\left(2,-1 \right)\), \(\left(2, -3\right)\)
    \(e = \frac{\sqrt{6}}{6}\)

15. \(\dfrac{(x - 3)^{2}}{9} + \dfrac{(y - 7)^{2}}{25} = 1\)
16. \(\dfrac{x^{2}}{39} + \dfrac{y^{2}}{64} = 1\)
17. \(\dfrac{x^{2}}{34} + \dfrac{y^{2}}{25} = 1\)
18. \(\dfrac{(x - 8)^{2}}{25} + \dfrac{(y - 2)^{2}}{4} = 1\)
19. \(\dfrac{(x-5)^{2}}{25} + \dfrac{4(y-2)^{2}}{75} = 1\)
20. \(\dfrac{(x - 8)^{2}}{64} + \dfrac{(y + 9)^{2}}{81} = 1\)
21. Jamie and Jason should stand \(100-25\sqrt{7} \approx 33.86\) feet from opposite ends of the gallery.
22. The arch can be modeled by the top half of \(\frac{x^2}{9} + \frac{y^2}{81} = 1\). One foot in from the base of the arch corresponds to either \(x = \pm 2\). Plugging in \(x = \pm 2\) gives \(y = \pm 3\sqrt{5}\) and since \(y\) represents a height, we choose \(y=3\sqrt{5} \approx 6.71\) feet.

23. Distance from the sun to aphelion \(\approx 1.0167\) AU.
    Distance from the sun to perihelion \(\approx 0.9833\) AU.

Reference

¹ This was foreshadowed in Exercise 19 in Section 7.2.

² The equation of a parabola has only one squared variable and the equation of a circle has two squared variables with identical coefficients.