1.4: Absolute value inequalities
- Page ID
- 48950
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Using the notation from the previous section, we now solve inequalities involving the absolute value. These inequalities may be solved in three steps:
- Step 1: Solve the corresponding equality. The solution of the equality divides the real number line into several subintervals.
- Step 2: Using step 1, check the inequality for a number in each of the subintervals. This check determines the intervals of the solution set.
- Step 3: Check the endpoints of the intervals.
Here are some examples for the above solution method.
Solve for \(x\):
- \(|x+7|<2\)
- \(|3x-5|\geq 11\)
- \(|12-5x|\leq 1\)
Solution
- We follow the three steps described above. In step 1, we solve the corresponding equality, \(|x+7|=2\). \(x+7=2\) & \(x+7=-2\) \[\begin{array}{l|l}
x+7=2 & x+7=-2 \\
\Longrightarrow x=-5 & \Longrightarrow x=-9
\end{array} \nonumber \]The solutions \(x=-5\) and \(x=-9\) divide the number line into three subintervals:
Now, in step 2, we check the inequality for one number in each of these subintervals.
\[ \begin{array}{c|c|c}
\text { Check: } \quad x=-10 & \text { Check: } \quad x=-7 & \text { Check: } \quad x=0 \\
|(-10)+7| \stackrel{?}{<} 2 & |(-7)+7| \stackrel{?}{<} 2 & |0+7| \stackrel{?}{<} 2 \\
|-3| \stackrel{?}{<} 2 & |0| \stackrel{?}{<} 2 & |7| \stackrel{?}{<} 2 \\
3 \stackrel{?}{<} 2 & 0 \stackrel{?}{<} 2 & 7 \stackrel{?}{<} 2 \\
\text { false } & \text { true } & \text { false }
\end{array} \nonumber \]
Since \(x=-7\) in the subinterval given by \(-9<x<-5\) solves the inequality \(|x+7|<2\), it follows that all numbers in the subinterval given by \(-9<x<-5\) solve the inequality. Similarly, since \(x=-10\) and \(x=0\) do not solve the inequality, no number in these subintervals will solve the inequality. For step 3, we note that the numbers \(x=-9\) and \(x=-5\) are not included as solutions since the inequality is strict (that is we have \(<\) instead of \(\leq\)).The solution set is therefore the interval \(S=(-9,-5)\). The solution on the number line is:
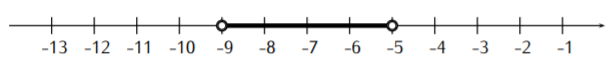
- We follow the steps as before. First, in step 1, we solve \(|3x-5|=11\). \[\begin{array}{l|l}
3 x-5=11 & 3 x-5=-11 \\
\Longrightarrow 3 x=16 & \Longrightarrow 3 x=-6 \\
\Longrightarrow x=\dfrac{16}{3} & \Longrightarrow x=-2
\end{array} \nonumber \]
The two solutions \(x=-2\) and \(x=\dfrac{16}{3}=5\dfrac {1}{3}\) divide the number line into the subintervals displayed below. \[x<-2 \hspace{1in} -2<x<5\frac 1 3 \hspace{1in} 5\frac 1 3<x \nonumber\]

For step 2, we check a number in each subinterval. This gives:
\[\begin{array}{c|c|c|c}
\text { Check: } x=-3 & \text { Check: } \quad x=1 & \text { Check: } \quad x=6 \\
|3 \cdot(-3)-5| \stackrel{?}{\geq} 11 & |3 \cdot 1-5| \stackrel{?}{\geq} 11 & |3 \cdot 6-5| \stackrel{?}{\geq} 11 \\
|-9-5| \stackrel{?}{\geq} 11 & |3-5| \stackrel{?}{\geq} 11 & |18-5| \stackrel{?}{\geq} 11 \\
|-14| \stackrel{?}{\geq} 11 & |-2| \stackrel{?}{\geq} 11 & |13| \stackrel{?}{\geq} 11 \\
14 \stackrel{?}{\geq} 11 & 2 \stackrel{?}{\geq} 11 & 13 \stackrel{?}{\geq} 11 \\
\text { true } & \text { false } & \text { true }
\end{array} \nonumber \]
For step 3, note that we include \(-2\) and \(5\dfrac {1}{3}\) in the solution set since the inequality is “greater than or equal to” (that is \(\geq\), as opposed to \(>\)). Furthermore, the numbers \(-\infty\) and \(\infty\) are not included, since \(\pm\infty\) are not real numbers.
The solution set is therefore the union of the two intervals: \[S=\Big(-\infty,-2\Big]\cup \Big[5\dfrac {1}{3}, \infty\Big) \nonumber \]
- To solve \(|12-5x|\leq 1\), we first solve the equality \(|12-5x|=1\). \[\begin{array}{l|l}
12-5 x=1 & 12-5 x=-1 \\
\Longrightarrow-5 x=-11 & \Longrightarrow-5 x=-13 \\
\Longrightarrow x=\frac{-11}{-5}=2.2 & \Longrightarrow x=\frac{-13}{-5}=2.6
\end{array} \nonumber \]
This divides the number line into three subintervals, and we check the original inequality \(|12-5x|\leq 1\) for a number in each of these subintervals.
\[\begin{array}{c|c|c|c}
\text {Interval: } \quad x<2.2 & \text {Interval: } \quad 2.2<x<2.6 & \text {Interval: } \quad 2.6<x\\
\text {Check: } \quad x=1 & \text {Check: } \quad x=2.4 & \text {Check: } \quad x=3 \\
|12-5 \cdot 1| \stackrel{?}{\leq} 1 & |12-5 \cdot 1| \stackrel{?}{\leq} 1 & |12-5 \cdot 3| \stackrel{?}{\leq} 1 \\
|12-5| \stackrel{?}{\leq} 1 & |12-12| \stackrel{?}{\leq} 1 & |12-15| \stackrel{?}{\leq} 1 \\
|7| \stackrel{?}{\leq} 1 & |0| \stackrel{?}{\leq} 1 & |-3| \stackrel{?}{\leq} 1 \\
7 \stackrel{?}{\leq} 1 & 0 \stackrel{?}{\leq} 1 & 3 \stackrel{?}{\leq} 1 \\
\text { false } & \text { true } & \text { false }
\end{array} \nonumber \]
The solution set is the interval \(S=[2.2,2.6]\), where we included \(x=2.2\) and \(x=2.6\) since the original inequality “less than or equal to” (\(\leq\)) includes the equality.
Alternatively, whenever you have an absolute value inequality you can turn it into two inequalities.
Here are a couple of examples.
Solve for \(x\): \(|12-5x|\leq 1\)
Solution
Note that \(|12-5x|\leq 1\) implies that
\[-1\leq 12-5x\leq1 \nonumber \]
so that
\[-13\leq -5x\leq -11 \nonumber \]
and by dividing by \(-5\) (remembering to switch the direction of the inequalities when multiplying or dividing by a negative number) we see that
\[\frac{13}{5}\geq x\geq \frac{11}{5} \nonumber \]
or in interval notation, we have the solution set
\[S=\left[\frac{11}{5},\frac{13}{5}\right] \nonumber\]
If \(|x+6|>2\) then either \(x+6>2\) or \(x+6<-2\) so that either \(x>-4\) or \(x<-8\) so that in interval notation the solution is \(S=(-\infty,-8)\cup(-4,\infty)\).
Solution
There is a geometric interpretation of the absolute value on the number line as the distance between two numbers:

distance between \(a\) and \(b\) is \(|b-a|\) which is also equal to \(|a-b|\)
This interpretation can also be used to solve absolute value equations and inequalities.
Solve for \(x\):
- \(|x-6|=4\)
- \(|x-6|\leq 4\)
- \(|x-6|\geq 4\)
Solution
- Consider the distance between \(x\) and \(6\) to be \(4\) on a number line:

There are two solutions, \(x=2\) or \(x=10\). That is, the distance between \(2\) and \(6\) is \(4\) and the distance between \(10\) and \(6\) is \(4\).
- Numbers inside the braces above have distance \(4\) or less. The solution is given on the number line as:

In interval notation, the solution set is the interval \(S=[2,10]\). One can also write that the solution set consists of all \(x\) such that \(2\leq x\leq 10\).
- Numbers outside the braces above have distance \(4\) or more. The solution is given on the number line as:

In interval notation, the solution set is the interval \((-\infty,2]\) and \([10,\infty)\), or in short it is the union of the two intervals:
\[S= (\infty,2]\cup [10,\infty) \nonumber \]
One can also write that the solution set consists of all \(x\) such that \(x\leq 2\) or \(x\geq 10\).


