10.1: Optional section- The rational root theorem
- Page ID
- 49010
Consider the equation \(10x^3-6x^2+5x-3=0\). Let \(x\) be a rational solution of this equation, that is \(x=\dfrac p q\) is a rational number such that
\[10\cdot\Big(\dfrac p q\Big)^3-6\cdot\Big(\dfrac p q\Big)^2+5\cdot\dfrac p q-3=0 \nonumber \]
We assume that \(x=\dfrac p q\) is completely reduced, that is, \(p\) and \(q\) have no common factors that can be used to cancel the numerator and denominator of the fraction \(\dfrac p q\). Now, simplifying the above equation, and combining terms, we obtain:
\[\begin{aligned} && 10\cdot\dfrac {p^3} {q^3}-6\cdot\dfrac {p^2} {q^2}+5\cdot\dfrac p q-3 = 0\\ \text{(multiply by $q^3$)} &\implies & 10 p^3-6p^2q+5pq^2-3q^3 =0\\ \text{(add $3q^3$)} &\implies & 10 p^3-6p^2q+5pq^2=3q^3 \\ \text{(factor $p$ on the left)} &\implies & p\cdot(10 p^2-6pq+5q^2)=3q^3 \end{aligned} \nonumber \]
Therefore, \(p\) is a factor of \(3q^3\) (with the other factor being \((10 p^2-6pq+5q^2)\)). Since \(p\) and \(q\) have no common factors, \(p\) must be a factor of \(3\). That is, \(p\) is one of the following integers: \(p=+1, +3, -1, -3\)
Similarly starting from \(10 p^3-6p^2q+5pq^2-3q^3 =0\), we can write
\[\begin{aligned} \text{(add $+6p^2q-5pq^2+3q^3 $)} &\implies & 10 p^3=6p^2q-5pq^2+3q^3 \\ \text{(factor $q$ on the right)} &\implies & 10 p^3=(6p^2-5pq+3q^2)\cdot q \end{aligned}\]
Now, \(q\) must be a factor of \(10p^3\). Since \(q\) and \(p\) have no common factors, \(q\) must be a factor of \(10\). In other words, \(q\) is one of the following numbers: \(q=\pm1, \pm 2, \pm 5, \pm 10\). Putting this together with the possibilities for \(p=\pm 1, \pm 3\), we see that all possible rational roots are the following:
\[\pm\dfrac{1}{1},\quad \pm\dfrac{1}{2},\quad \pm\dfrac{1}{5},\quad \pm\dfrac{1}{10},\quad \pm\dfrac{3}{1},\quad \pm\dfrac{3}{2},\quad \pm\dfrac{3}{5},\quad \pm\dfrac{3}{10} \nonumber \]
The observation in the previous example holds for a general polynomial equation with integer coefficients.
Consider the equation \[a_n x^n+a_{n-1}x^{n-1}+\dots + a_1 x + a_0=0 \label{EQnthorder} \]
where every coefficient \(a_n, a_{n-1},\dots, a_0\) is an integer and \(a_0\neq 0\), \(a_n\neq 0\). Assume that \(x=\dfrac p q\) is a solution of \(\ref {EQnthorder}\) and the fraction \(x=\dfrac p q\) is completely reduced. Then \(a_0\) is an integer multiple of \(p\), and \(a_n\) is an integer multiple of \(q\).
Therefore, all possible rational solutions of \(\ref {EQnthorder}\) are fractions \(x=\dfrac p q\) where \(p\) is a factor of \(a_0\) and \(q\) is a factor of \(a_n\).
We can use this observation to find good candidates for the roots of a given polynomial.
- Find all rational roots of \(f(x)=7x^3+x^2+7x+1\).
- Find all real roots of \(f(x)=2x^3+11x^2-2x-2\).
- Find all real roots of \(f(x)=4x^4-23x^3-2x^2-23x-6\).
Solution
- If \(x=\dfrac p q\) is a rational root, then \(p\) is a factor of \(1\), that is \(p=\pm1\), and \(q\) is a factor of \(7\), that is \(q=\pm 1, \pm 7\). The candidates for rational roots are therefore \(x=\pm \dfrac 1 1, \pm \dfrac 1 7\). To see which of these candidates are indeed roots of \(f\) we plug these numbers into \(f\) via the calculator. We obtain the following:
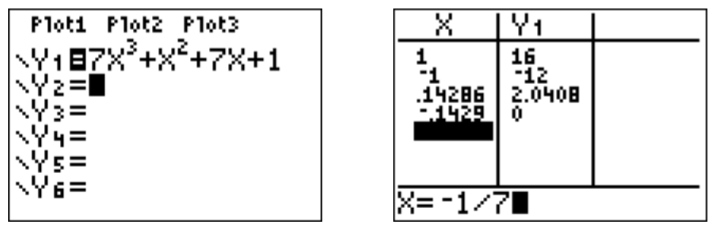
Note that we entered the \(x\)-value as a fraction “\((-)1/7\)” on the right. The only root among \(\pm 1, \pm \dfrac 1 7\) is \(x=-\dfrac 1 7\).
- We need to identify all real roots of \(f(x)=2x^3+11x^2-2x-2\). In general, it is a quite difficult task to find a root of a polynomial of degree \(3\), so that it will be helpful if we can find the rational roots first. If \(x=\dfrac p q\) is a rational root then \(p\) is a factor of \(-2\), that is \(p=\pm 1, \pm 2\), and \(q\) is a factor of \(2\), that is \(q=\pm 1, \pm 2\). The possible rational roots \(x=\dfrac p q\) of \(f\) are: \[\pm 1, \quad \pm 2, \quad \pm \dfrac 1 2 \nonumber \] Using the calculator, we see that the only rational root is \(x=\dfrac 1 2\).
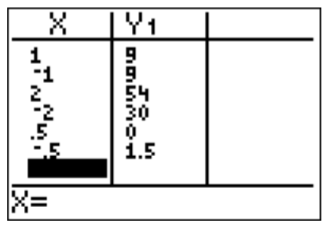
Therefore, by the factor theorem (Observation Remainder), we see that \(\left (x-\dfrac 1 2 \right )\) is a factor of \(f\), that is \(f(x)=q(x)\cdot \left (x-\dfrac 1 2 \right )\). To avoid fractions in the long division, we rewrite this as \[f(x)=q(x)\cdot \left (x-\dfrac 1 2 \right )=q(x)\cdot \dfrac{2x-1}{2}=\dfrac{q(x)}2 \cdot(2x-1) \nonumber \] so that we may divide \(f(x)\) by \((2x-1)\) instead of \(\left (x-\dfrac 1 2 \right )\) (note that this can not be done with synthetic division). We obtain the following quotient.
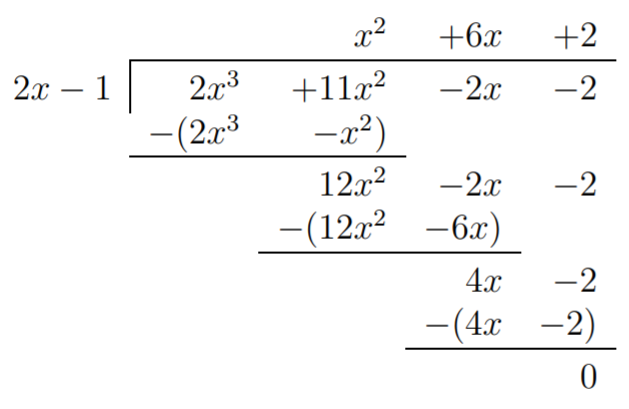
Therefore, \(f(x)=(x^2+6x+2)(2x-1)\), and any root of \(f\) is either a root of \(x^2+6x+2\) or of \(2x-1\). We know that the root of \(2x-1\) is \(x=\dfrac 1 2\), and that \(x^2+6x+2\) has no other rational roots. Nevertheless, we can identify all other real roots of \(x^2+6x+2\) via the quadratic formula, (see Theorem for Quadratic Formula).
\[\begin{aligned} x^2+6x+2=0 \quad \implies \quad x_{1/2} & = & \dfrac{-6\pm\sqrt{6^2-4\cdot 1\cdot 2}}{2}\\ &=& \dfrac{-6\pm\sqrt{36-8}}{2}=\dfrac{-6\pm\sqrt{28}}{2}\\ &=& \dfrac{-6\pm\sqrt{4\cdot 7}}{2}=\dfrac{-6\pm2\sqrt{7}}{2}\\ &=& -3\pm\sqrt{7}\end{aligned} \nonumber \]
Therefore, the roots of \(f\) are precisely the following \[x_1=-3+\sqrt{7}, \quad x_2=-3-\sqrt{7}, \quad x_3=\dfrac 1 2 \nonumber \]
- First we find the rational roots \(x=\dfrac p q\) of \(f(x)=4x^4-23x^3-2x^2-23x-6\). Since \(p\) is a factor of \(-6\) it must be \(p=\pm 1, \pm 2, \pm 3, \pm 6\), and since \(q\) is a factor of \(4\) it must be \(q=\pm 1, \pm 2, \pm 4\). All candidates for rational roots \(x=\dfrac p q\) are the following (where we excluded repeated ways of writing \(x\)): \[\pm 1,\quad \pm 2,\quad \pm 3,\quad \pm 6,\quad \pm \dfrac 1 2,\quad \pm \dfrac 3 2,\quad \pm \dfrac 1 4,\quad \pm \dfrac 3 4 \nonumber \] Checking all these candidates with the calculator produces exactly two rational roots: \(x=6\) and \(x=-\dfrac 1 4\). Therefore, we may divide \(f(x)\) by both \((x-6)\) and by \(\left(x+\dfrac 1 4 \right)\) without remainder. To avoid fractions, we use the term \(4\cdot \left(x+\dfrac 1 4 \right)=(4x+1)\) instead of \(\left(x+\dfrac 1 4 \right)\) for our factor of \(f\). Therefore, \(f(x)=q(x)\cdot (x-6)\cdot (4x+1)\). The quotient \(q(x)\) is determined by performing a long division by \((x-6)\) and then another long division by \((4x+1)\), or alternatively by only one long division by \[(x-6)\cdot (4x+1)=4x^2+x-24x-6=4x^2-23x-6 \nonumber \] Dividing \(f(x)=4x^4-23x^3-2x^2-23x-6\) by \(4x^2-23x-6\) produces the quotient \(q(x)\):
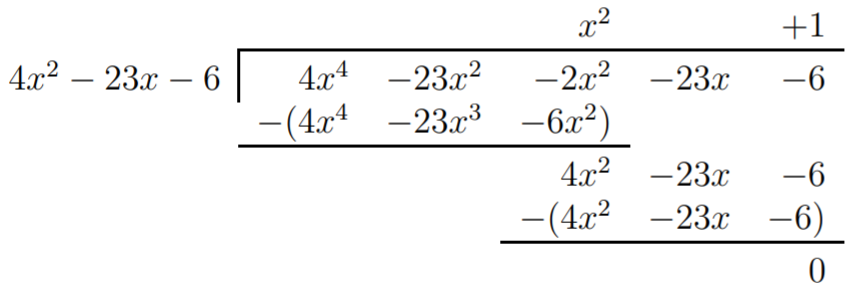
We obtain the factored expression for \(f(x)\) as \(f(x)= (x^2+1)(4x+1)(x-6)\). The only remaining real roots we need to find are those of \(x^2+1\). However, \[x^2+1=0 \quad\implies \quad x^2=-1 \nonumber \] has no real solution. In other words there are only complex solutions of \(x^2=-1\), which are \(x=i\) and \(x=-i\) (we will discuss complex solutions in more detail in the next section). Since the problem requires us to find the real roots of \(f\), our answer is that the only real roots are \(x_1=6\) and \(x_2=-\dfrac 1 4\).